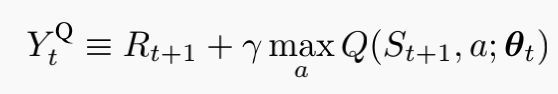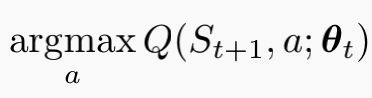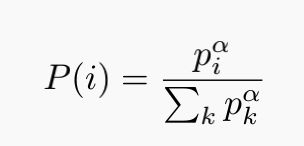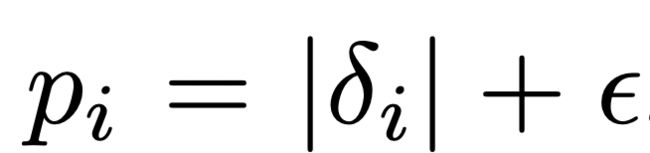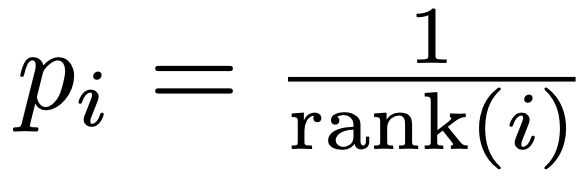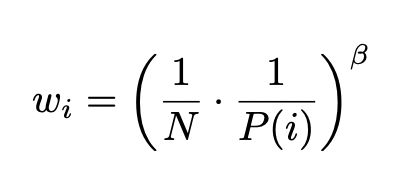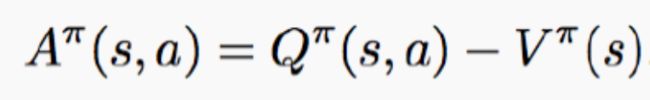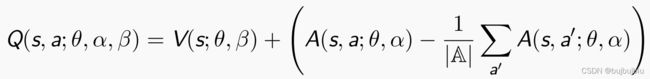DQN及其变种（Double DQN，优先回放，Dueling DQN)

1.DQN

1.1DQN的三大特点

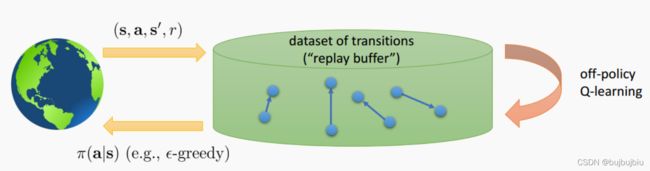
DQN由DeepMind在2013年发表的文章《Playing Atari with Deep Reinforcement Learning》提出，文章有两个创新点：经验回放和设立单独的目标网络。DQN的大体框架是Q-learning。如图为Q-learning的伪代码。

Q-learning有两个关键概念：异策略和时间差分

• 异策略：行动策略（产生数据的策略）和评估策略不是同一个策略。从上图伪代码中看出，行动策略使用的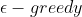策略，而评估改进的目标策略为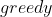，即选择使行为值函数最大的动作。
• 时间差分：利用时间差分目标更新当前行为值函数。时间差分目标为

DQN对Q-learning修改体现在三个方面：

（1）DQN利用深度卷积神经网络逼近值函数(CNN)

DQN行为值函数利用神经网络逼近，属于非线性参数逼近，此处的值函数对应着一组参数，在神经网络中参数就是每层网络的权重，用表示，行为值函数表示为 。更新值函数也就是更新参数。当网络结构确定时，就代表值函数。DQN网络使用三个卷积层加两个全连接层。输入84✖️84✖️4的图像，在论文中网络结构和超参数都是固定的。

 但是使用神经网络逼近值函数常常出现不稳定不收敛的情况，为此构造了一种新的神经网络训练方法：经验回放

（2）DQN使用经验回放训练强化学习过程(Experience Replay)

经验回放能使神经网络的训练收敛且稳定，原因在于：训练神经网络时，提前假设为训练数据独立且同分布，但是通过强化学习采集到的数据存在关联性，利用这些数据进行顺序训练，神经网络自然会不稳定，而经验回放可以打破数据间的关联性。

在强化学习过程中，智能体将数据存储在一个数据库中，均匀随机采样的方式从数据库中抽取数据，然后利用抽取到的数据训练神经网络。经验池数据为，...

其实经验回放在之前就被提出，2015年的论文又提出了目标网络的方法，进一步降低了数据之间的关联性。

（3）DQN设置了目标网络来单独处理时间差分算法中的TD偏差（Target Network）

利用神经网络对值函数进行逼近时，值函数的更新步更新的是参数，DQN使用CNN和梯度下降法，因此原伪代码中的Q值更新变成了一次监督学习式的参数更新。为TD目标，计算时用到的网络参数为。

计算TD目标时所用的网络称为TD网络，在DQN之前，使用神经网络逼近值函数，计算TD目标的动作值函数所用的网络参数，和梯度计算中逼近的值函数所用的网络参数相同，容易导致数据间存在关联性。为此DeepMind团队提出计算TD目标的网络表示为，计算动作值函数逼近的网络表示为。用于动作值函数逼近的网络每一步都更新，用于TD目标网络的参数每固定步数更新一次。

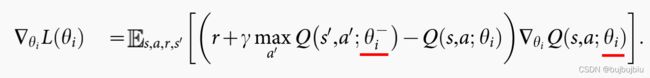 1.2DQN伪代码解读

（1）初始化回放记忆D，设置可容纳的数据条数为N 

（2）利用随机权重初始化动作值函数

（3）令权重来初始化TD目标的动作值函数

（4）循环每个episode，共M个episode

    （5）初始化episode序列的第一个状态，预处理得到状态对应的特征输入

    （6）循环每个episode的每一步，共T步

        （7）利用概率选择一个随机动作

        （8）如果概率随机选择没有发生，则用贪婪策略选择当前动作值函数最大的动作

        （9）在仿真器中执行，观察回报和图像（新状态）

        （10）设置，预处理

        （11）将转换储存在回放记忆D中

        （12）从D中均匀随机采样获得一个转换样本数据

        （13）判断是否是一个episode的终止状态，若是则TD目标为，否则利用TD目标网络计算TD目标

        （14）在网络参数上执行一次梯度下降算法

        （15）更新动作值函数的网络参数

        （16）每隔C步更新一次TD目标网络权值，

    （17）结束一次episode内循环

（18）结束所有episode间循环

（7）（8）为行动策略即

（8）中选择最大动作时的动作值函数网络和TD目标网络参数相同，初始化阶段，训练后不同

（12）体现经验回放

（13）使用独立目标网络计算TD目标值

（15）（16）和更新频次不同

2.Double DQN

《Deep Reinforcement Learning with Double Q-learning》

DQN无法克服Q-learning本身固有的缺点——过估计。过估计是指估计的值函数比真实的值函数大，Q-learning存在过估计的原因在于max操作，不管是表格型还是函数逼近，值函数更新公式都离不开max。

如果值函数每一点的值都过估计了相同的幅度，即过估计量是均匀的，由于最优策略是贪婪策略，即找到最大动作值函数的动作，这时最优策略是保持不变的。强化学习最终目标是找到最优策略而非值函数，也就是说，即便值函数被过估计了，对结果是不影响的。但是问题在于过估计量是不均匀的，这会导致得出的最优策略可能只是次优。

为了解决值函数过估计的问题，Hasselt等提出了Double Q-learning，即 将动作的选择和动作的评估用不同的值函数实现。

• 动作选择

Q-learning值函数更新公式如下，在求解TD目标时先要选择一个动作，满足在状态处最大，这叫动作选择。 

•  动作评估

选出后，利用的动作值函数构造TD目标。

Q-learning使用同一个参数来选择和评估动作，Double Q-learning用不同的动作值函数来选择和评估动作。Double Q-learning的TD目标如下，

 y=f(t) ：一般的函数形式

y=max f(t) ：y是f(t)函数的最大值

y=argmax f(t) ：y是f(t)函数取到最大值时的参数t

从公式看出，动作选择的动作值函数如下，网络参数为，选出最大动作后再评估，这时的动作值函数网络参数为

​

将Double Q-learning的思想融合到DQN中，就得到Double DQN，其TD目标为

​

与Double Q-learning相比，第二个网络由目标网络代替，以此来评估当前贪婪策略，目标网络的更新同DQN一保持不变，即在线网络的周期性复制。 

3.优先回放（Prioritized Reply） 

《PRIORITIZED EXPERIENCE REPLAY》

DQN使用经验回放和独立目标网络，Double DQN改进了DQN中的max操作，但是经验回放还是采用均匀分布。但是智能体的经验（历史数据）对于智能体的学习并非相同的效率，在某些状态下，智能体的学习效率更高。优先回放的基本思想是打破均匀分布，赋予学习效率高的状态以更大的采样权重。

如何选择权重？理想标准是学习效率越高，权重越大。TD偏差越大，说明该状态处的值函数与TD目标的差距越大，智能体更新量越大，因此该处的学习效率越高。设样本​处的TD偏差为​，则该样本处的采样概率为：

​由TD偏差​决定，一般有两种方法：其中​根据​的绝对值排序得到

采用优先回放的概率分布采样，动作值函数的估计是一个有偏估计，因为采样分布和动作值函数分布是两个完全不同的分布，为了矫正这个偏差，需要乘一个重要性采样系数：

带有优先回放的DDQN伪代码如下： 

​

（1）输入：minibatch大小为k，步长为​，回放周期K，存储数据大小N，常数​，​，总时间T

（2）初始化经验回放库​，​，​

（3）观察初始状态​，选择动作​

（4）时间t从1到T，进入循环

    （5）观察​

    （6）将数据​存储在经验回放库中，令其优先级为​，采用该优先级初始化的目的是保证每个样本至少被利用一次

    （7）每隔K步回放一次

        （8）依次采集k个样本，循环一个minibatch

            （9）根据概率分布采样一个样本点（需要对p的所有样本排序）

            （10）计算该样本的重要性权重​

            （11）更新该样本点的TD偏差​

            （12）根据TD偏差更新该样本点的优先级​

            （13）累计权重改变量​

          (14) 结束本样本权重，采样下一个样本

        （15）采样并处理完k个样本后更新权重值​，重新设置​

        （16）按步长更新目标网络的权重

    （17）结束一次更新

    （18）根据新策略选择下一个动作

（19）将新动作作用于环境，得到新数据，进入新循环

下图为文章中的神经网络结构设计 

​

4.Dueling DQN

DQN，Double DQN，经验优先回放DQN，在值函数逼近时都是使用卷积神经网络，Dueling DQN从网络结构改变了DQN，动作值函数可以分解为状态值函数和优势函数，如图所示，原先卷积层后面直接跟着全连接层，输出Q值，而Dueling DQN中，使用两个全连接序列，单独估计状态值函数和优势函数，最后汇总输出单一Q值。结合两个完全连接层流输出Q估计的模块需要非常周到的设计。

优势函数是什么？公式中被称为优势函数。

值函数是在状态s下所有可能动作的动作值函数乘采取该动作的概率和，即值函数是该状态下所有动作值函数关于动作概率的平均值。

而动作值函数是单个动作对应的值 ，能评价当前动作值函数相对于平均值的大小，因此此处的优势是动作值函数相比于当前状态的值函数的优势，如果优势函数大于0，说明该动作比平均动作好，反之说明当前动作不如平均动作好。

Dueling DQN网络输出组成：

​为卷积层参数，为状态值函数网络参数，为优势函数网络参数。此处的优势函数做了中心化的处理，保证在某动作下会出现零优势。

Dueling DQN是在DQN基础上对神经网络结构部分进行修改，其余流程与DQN相似。

参考文献：

《Playing Atari with Deep Reinforcement Learning》

《Deep Reinforcement Learning with Double Q-learning》

《PRIORITIZED EXPERIENCE REPLAY》

《Dueling Network Architectures for Deep Reinforcement Learning》

以上文章均来自https://arxiv.org/abs