深度学习入门之SGD随机梯度下降法

SGD

SGD为随机梯度下降法。用数学式可以将 SGD 写成如下的式（6.1）。

这里把需要更新的权重参数记为W，把损失函数关于W的梯度记为 ∂L/∂W 。$\eta$ 表示学习率，实际上会取 0.01 或 0.001 这些事先决定好的值。式子中的←表示用右边的值更新左边的值。

如式（6.1）所示，SGD 是朝着梯度方向只前进一定距离的简单方法。现在，将 SGD 实现为一个 Python 类（为方便后面使用，将其实现为一个名为 SGD 的类）。

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr#学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

进行初始化时的参数 lr 表示 learning rate（学习率）。这个学习率会保存为实例变量。此外，代码段中还定义了 update(params, grads) 方法，这个方法在 SGD 中会被反复调用。

参数 params 和 grads 是字典型变量，按 params[‘W1’] 、grads[‘W1’] 的形式，分别保存了权重参数和它们对应的梯度。

使用这个 SGD 类，可以按如下方式进行神经网络的参数的更新（下面的代码是不能实际运行的伪代码）。

network = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000):#更新次数
    ...
    x_batch, t_batch = get_mini_batch(...) # mini-batch
    grads = network.gradient(x_batch, t_batch)
    params = network.params
    optimizer.update(params, grads)
    ...

这里首次出现的变量名 optimizer 表示“进行最优化的人”的意思，这里由 SGD 承担这个角色。参数的更新由 optimizer 负责完成。我们在这里需要做的只是将参数和梯度的信息传给 optimizer 。

SGD的缺点

虽然 SGD 简单，并且容易实现，但是在解决某些问题时可能没有效率。这里，在指出 SGD 的缺点之际，我们来思考一下求下面这个函数的最小值的问题。

如图 6-1 所示，式（6.2）表示的函数是向 x 轴方向延伸的“碗”状函数。实际上，式（6.2）的等高线呈向 x 轴方向延伸的椭圆状。

图 6-1　 的图形（左图）和它的等高线（右图）

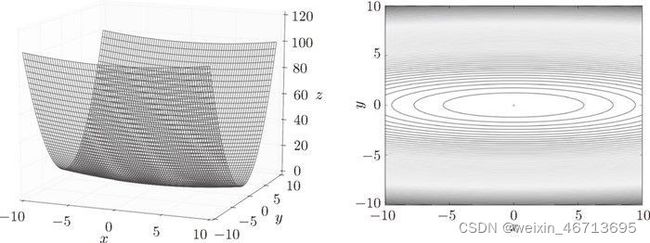
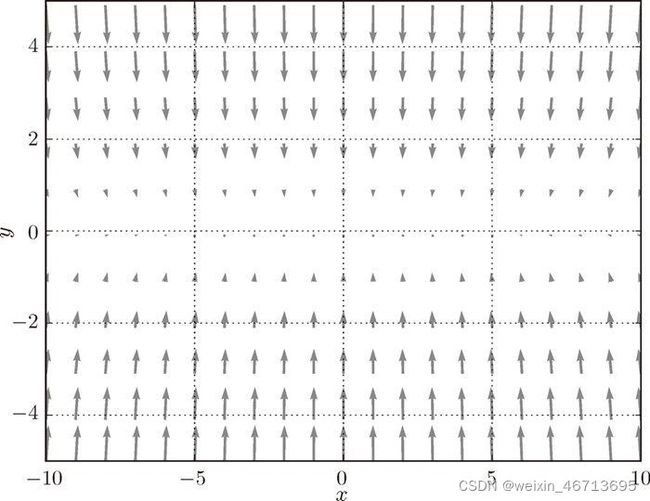
现在看一下式（6.2）表示的函数的梯度。如果用图表示梯度的话，则如图 6-2 所示。这个梯度的特征是，$y$ 轴方向上大，$x$ 轴方向上小。换句话说，就是 $y$ 轴方向的坡度大，而 $x$ 轴方向的坡度小。

这里需要注意的是，虽然式 (6.2) 的最小值在 $(x,y)=(0,0)$ 处，但是图 6-2 中的梯度在很多地方并没有指向 $(0,0)$。

图 6-2 f(x,y)=1/20 x^2 + y^2的梯度

我们来尝试对图 6-1 这种形状的函数应用 SGD。从 $(x,y)=(-7.0,2.0)$ 处（初始值）开始搜索，结果如图 6-3 所示。

图 6-3　基于 SGD 的最优化的更新路径：呈“之”字形朝最小值 (0, 0) 移动，**效率低**

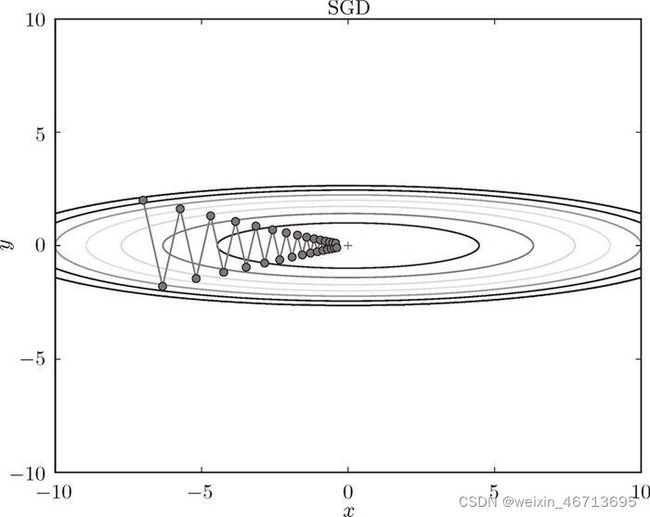
在图 6-3 中，SGD 呈“之”字形移动。这是一个相当低效的路径。也就是说，SGD 的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的 SGD 更聪明的方法。

SGD 低效的根本原因是，梯度的方向并没有指向最小值的方向。为了改正SGD的缺点，引入了Momentum、AdaGrad、Adam这 3 种方法来取代SGD。