《黑书》后缀数组学习笔记......

最近看黑书看到数据结构之后缀数组了，以前没有搞过后缀数组，初学起来感觉比较难，网上参考了两种后缀数组学习笔记，以及罗穗骞倍增算法代码，这里附上链接：http://tieba.baidu.com/f?kz=754580296

http://www.cnblogs.com/staginner/archive/2012/02/02/2335600.html

http://wenku.baidu.com/view/ed1be61e10a6f524ccbf85fd.html

他们的都是纯文字说明，这里我按照自己的理解方式，附上自己的数据.......

这是模版：

int wa[maxn],wb[maxn],wv[maxn],ws[maxn];

int cmp(int *r,int a,int b,int l)

{return r[a]==r[b]&&r[a+l]==r[b+l];}

void da(int *r,int *sa,int n,int m)

{

int i,j,p,*x=wa,*y=wb,*t;

for(i=0;i<m;i++) ws[i]=0;

for(i=0;i<n;i++) ws[x[i]=r[i]]++;

for(i=1;i<m;i++) ws[i]+=ws[i-1];

for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;

for(j=1,p=1;p<n;j*=2,m=p)

{

for(p=0,i=n-j;i<n;i++) y[p++]=i;

for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;

for(i=0;i<n;i++) wv[i]=x[y[i]];

for(i=0;i<m;i++) ws[i]=0;

for(i=0;i<n;i++) ws[wv[i]]++;

for(i=1;i<m;i++) ws[i]+=ws[i-1];

for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];

for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)

x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;

}

return;

}

 

int wa[maxn],wb[maxn],wv[maxn],ws[maxn];

int cmp(int *r,int a,int b,int l)

{return r[a]==r[b]&&r[a+l]==r[b+l];}  //就像论文所说，由于末尾填了0，所以如果r[a]==r[b]（实际是y[a]==y[b]），说明待合并的两个长为j的字符串，前面那个一定不包含末尾0，因而后面这个的起始位置至多在0的位置，不会再靠后了，因而不会产生数组越界。

//da函数的参数n代表字符串中字符的个数，这里的n里面是包括人为在字符串末尾添加的那个0的，但论文的图示上并没有画出字符串末尾的0。

//da函数的参数m代表字符串中字符的取值范围，是基数排序的一个参数，如果原序列都是字母可以直接取128，如果原序列本身都是整数的话，则m可以取比最大的整数大1的值。

void da(int *r,int *sa,int n,int m)

{

    int i,j,p,*x=wa,*y=wb,*t;

    //以下四行代码是把各个字符（也即长度为1的字符串）进行基数排序，如果不理解为什么这样可以达到基数排序的效果，不妨自己实际用纸笔模拟一下，我最初也是这样才理解的。

    for(i=0;i<m;i++) ws[i]=0;

    for(i=0;i<n;i++) ws[x[i]=r[i]]++;  //x[]里面本意是保存各个后缀的rank值的，但是这里并没有去存储rank值，因为后续只是涉及x[]的比较工作，因而这一步可以不用存储真实的rank值，能够反映相对的大小即可。

    for(i=1;i<m;i++) ws[i]+=ws[i-1];

    for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;  //i之所以从n-1开始循环，是为了保证在当字符串中有相等的字符串时，默认靠前的字符串更小一些。

    //下面这层循环中p代表rank值不用的字符串的数量，如果p达到n，那么各个字符串的大小关系就已经明了了。

    //j代表当前待合并的字符串的长度，每次将两个长度为j的字符串合并成一个长度为2*j的字符串，当然如果包含字符串末尾具体则数值应另当别论，但思想是一样的。

    //m同样代表基数排序的元素的取值范围

    for(j=1,p=1;p<n;j*=2,m=p)

    {

        //以下两行代码实现了对第二关键字的排序

        for(p=0,i=n-j;i<n;i++) y[p++]=i;  //结合论文的插图，我们可以看到位置在第n-j至n的元素的第二关键字都为0，因此如果按第二关键字排序，必然这些元素都是排在前面的。

        for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;  //结合论文的插图，我们可以看到，下面一行的第二关键字不为0的部分都是根据上面一行的排序结果得到的，且上一行中只有sa[i]>=j的第sa[i]个字符串（这里以及后面指的“第?个字符串”不是按字典序排名来的，是按照首字符在字符串中的位置来的）的rank才会作为下一行的第sa[i]-j个字符串的第二关键字，而且显然按sa[i]的顺序rank[sa[i]]是递增的，因此完成了对剩余的元素的第二关键字的排序。

        //第二关键字基数排序完成后，y[]里存放的是按第二关键字排序的字符串下标

        for(i=0;i<n;i++) wv[i]=x[y[i]];  //这里相当于提取出每个字符串的第一关键字（前面说过了x[]是保存rank值的，也就是字符串的第一关键字），放到wv[]里面是方便后面的使用

        //以下四行代码是按第一关键字进行的基数排序

        for(i=0;i<m;i++) ws[i]=0;

        for(i=0;i<n;i++) ws[wv[i]]++;

        for(i=1;i<m;i++) ws[i]+=ws[i-1];

        for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];  //i之所以从n-1开始循环，含义同上，同时注意这里是y[i]，因为y[i]里面才存着字符串的下标

        //下面两行就是计算合并之后的rank值了，而合并之后的rank值应该存在x[]里面，但我们计算的时候又必须用到上一层的rank值，也就是现在x[]里面放的东西，如果我既要从x[]里面拿，又要向x[]里面放，怎么办？当然是先把x[]的东西放到另外一个数组里面，省得乱了。这里就是用交换指针的方式，高效实现了将x[]的东西“复制”到了y[]中。

        for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)

        x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //这里就是用x[]存储计算出的各字符串rank的值了，记得我们前面说过，计算sa[]值的时候如果字符串相同是默认前面的更小的，但这里计算rank的时候必须将相同的字符串看作有相同的rank，要不然p==n之后就不会再循环啦。

    }

    return;

}



//能够线性计算height[]的值的关键在于h[](height[rank[]])的性质，即h[i]>=h[i-1]-1，下面具体分析一下这个不等式的由来。

//论文里面证明的部分一开始看得我云里雾里，后来画了一下终于搞明白了，我们先把要证什么放在这：对于第i个后缀，设j=sa[rank[i] - 1]，也就是说j是i的按排名来的上一个字符串，按定义来i和j的最长公共前缀就是height[rank[i]]，我们现在就是想知道height[rank[i]]至少是多少，而我们要证明的就是至少是height[rank[i-1]]-1。

//好啦，现在开始证吧。

//首先我们不妨设第i-1个字符串（这里以及后面指的“第?个字符串”不是按字典序排名来的，是按照首字符在字符串中的位置来的）按字典序排名来的前面的那个字符串是第k个字符串，注意k不一定是i-2，因为第k个字符串是按字典序排名来的i-1前面那个，并不是指在原字符串中位置在i-1前面的那个第i-2个字符串。

//这时，依据height[]的定义，第k个字符串和第i-1个字符串的公共前缀自然是height[rank[i-1]]，现在先讨论一下第k+1个字符串和第i个字符串的关系。

//第一种情况，第k个字符串和第i-1个字符串的首字符不同，那么第k+1个字符串的排名既可能在i的前面，也可能在i的后面，但没有关系，因为height[rank[i-1]]就是0了呀，那么无论height[rank[i]]是多少都会有height[rank[i]]>=height[rank[i-1]]-1，也就是h[i]>=h[i-1]-1。

//第二种情况，第k个字符串和第i-1个字符串的首字符相同，那么由于第k+1个字符串就是第k个字符串去掉首字符得到的，第i个字符串也是第i-1个字符串去掉首字符得到的，那么显然第k+1个字符串要排在第i个字符串前面，要么就产生矛盾了。同时，第k个字符串和第i-1个字符串的最长公共前缀是height[rank[i-1]]，那么自然第k+1个字符串和第i个字符串的最长公共前缀就是height[rank[i-1]]-1。

//到此为止，第二种情况的证明还没有完，我们可以试想一下，对于比第i个字符串的字典序排名更靠前的那些字符串，谁和第i个字符串的相似度最高（这里说的相似度是指最长公共前缀的长度）？显然是排名紧邻第i个字符串的那个字符串了呀，即sa[rank[i]-1]。也就是说sa[rank[i]]和sa[rank[i]-1]的最长公共前缀至少是height[rank[i-1]]-1，那么就有height[rank[i]]>=height[rank[i-1]]-1，也即h[i]>=h[i-1]-1。

//证明完这些之后，下面的代码也就比较容易看懂了。

int rank[maxn],height[maxn];

void calheight(int *r,int *sa,int n)

{

    int i,j,k=0;

    for(i=1;i<=n;i++) rank[sa[i]]=i;  //计算每个字符串的字典序排名

    for(i=0;i<n;height[rank[i++]]=k)  //将计算出来的height[rank[i]]的值，也就是k，赋给height[rank[i]]。i是由0循环到n-1，但实际上height[]计算的顺序是由height[rank[0]]计算到height[rank[n-1]]。

    for(k?k--:0,j=sa[rank[i]-1];r[i+k]==r[j+k];k++);  //上一次的计算结果是k，首先判断一下如果k是0的话，那么k就不用动了，从首字符开始看第i个字符串和第j个字符串前面有多少是相同的，如果k不为0，按我们前面证明的，最长公共前缀的长度至少是k-1，于是从首字符后面k-1个字符开始检查起即可。

    return;

}



//最后再说明一点，就是关于da和calheight的调用问题，实际上在“小罗”写的源程序里面是如下调用的，这样我们也能清晰的看到da和calheight中的int n不是一个概念，同时height数组的值的有效范围是height[1]~height[n]其中height[1]=0，原因就是sa[0]实际上就是我们补的那个0，所以sa[1]和sa[0]的最长公共前缀自然是0。

da(r,sa,n+1,128);

calheight(r,sa,n);

有了上面的基础，再加上这幅图片吧：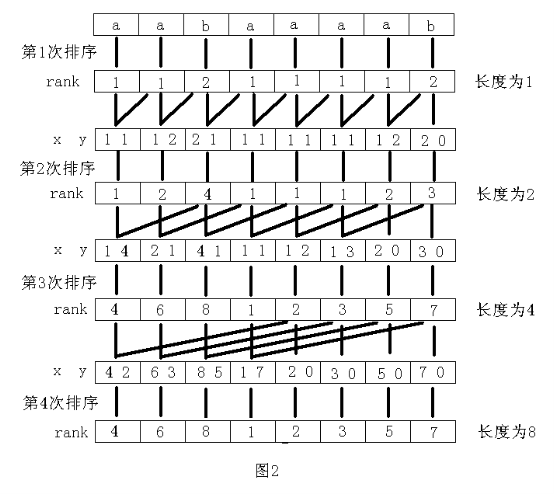

那么现在我的理解吧：

首先，我是通过测试数据，也就是手动运行来理解代码中各个变量以及整体代码的意思的，以aabaaaab为例

for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;

这四行代码是进行基数排序，r数组是原字符串数组的数值，x数组本意就是记录各个后缀的rank值，而这里只是反映其相应的rank关系。

弄完这四行代码，各个数组值：

ws[97]=6,ws[98]=8,其他的ws值为0；

x[0]=97  x[1]=97  x[2]=98  x[3]=97  x[4]=97  x[5]=97  x[6]=97  x[7]=98   对比图上第一次的关系，发现它可以反映相应的rank关系

sa[0]=0  sa[1]=1  sa[2]=3  sa[3]=4  sa[4]=5  sa[5]=6  sa[6]=2  sa[7]=7   这个数组记录了各个后缀所在位置，与图对应，

比如sa[0]=0，说的是，在只对对一关键字排序下，排在第0位的是字符串下标为0开始的字符后缀（这是第一次基数排序，长度为1）

比如s[6]=2，说的是，排在第六位的字符串下标为2（若是后面与前面的字符相等时，默认前面的字符排在前面，也就是默认前面的字符串更小）

 

//下面这层循环中p代表rank值不用的字符串的数量，如果p达到n，那么各个字符串的大小关系就已经明了了。
    //j代表当前待合并的字符串的长度，每次将两个长度为j的字符串合并成一个长度为2*j的字符串，当然如果包含字符串末尾具体则数值应另当别论，但思想是一样的。
    //m同样代表基数排序的元素的取值范围

 

 

for(p=0,i=n-j;i<n;i++)   y[p++]=i;  //结合论文的插图，我们可以看到位置在第n-j至n的元素的第二关键字都为0，因此如果按第二关键字排序，必然这些元素都是排在前面的。

y数组代表的含义，就是第二关键字排完所处在的位置，当然，首先要排除没有第二关键字的......也就是上一行所说的情况

 for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;

这两行代码运行完:
y[0]=7  y[1]=0  y[2]=2  y[3]=3  y[4]=4  y[5]=5  y[6]=1  y[7]=6

它所代表的含义就是第二关键字的排序后的相对顺序

比如说y[0]=7，就是第七个字符在这次排序中排在有第二关键的字符串的前面（因为第七个字符的第二关键字为0），

y[6]=1，就是第一个字符排在第六位.....为什么会是6呢？会发现有六个a，第一个位置的a排在第六位.....我是这样理解的，感觉不怎么对.....

for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];

这几行是对第二关键字进行基数排序........

wv数组记录第二关键字的相对rank值，它与第一关键字的rank值有关系，可以由上一级的x也就是相对rank值的关系得出......

wv[0]=98  wv[1]=97  wv[2]=98  wv[3]=97  wv[4]=97  wv[5]=97  wv[6]=97  wv[7]=97   对应第二关键字的rank

这里得注意，上面说道，在第二关键字排序的时候，有些第二关键字是不存在的，我们将有第二关键字的前面，也就是说，在这里，wv[0]排的会是最后一个字符b，因为它

没有第二关键字.......那么一次说，以后的rank值都往后退一位......比如wv[2]=98,表示的是排在原字符串中的第一个字符b.......

sa[0]=0  sa[1]=3  sa[2]=4  sa[3]=5  sa[4]=1  sa[5]=6  sa[6]=7  sa[7]=2

sa数组依旧存储第二关键字排好序之后，第几个字符排在第几位；

比如sa[7]=2，排在第7为的是原字符串中的第二个字符（从第0个开始）........

 

至此，可以总结一句，sa数组记录的是以哪个字符开头的字符串后缀排在哪一位；x也就是wa数组记录的是各自字符串后缀的rank值......

 

 

for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
        x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;

这两行代码，是将两个关键字的rank合并........

合并之后的x数组：x[0]=0  x[1]=4  x[2]=7  x[3]=1  x[4]=2  x[5]=3  x[6]=5  x[7]=6

字符：aa  ab  ba  aa  aa  aa ab b

下标：0    1    2   3    4   5  6   7

发现木有？下标为1的ab排在第四，下标为3的aa排在第一......所以说，x是保存其rank值的.......

 

height数组的值应该是从height[1]开始的，而且height[1]应该是等于0的。
原因是，+因为我们在字符串后面添加了一个0号字符，所以它必然是最小的
一个后缀。而字符串中的其他字符都应该是大于0的（前面有提到，使用倍
增算法前需要确保这点），所以排名第二的字符串和0号字符的公共前缀
（即height[1]）应当为0.

写到这里，数值分析基本完了，至于height函数，我是参考上面那位的详细解答才明白的.....这里就不再重复......