论文笔记ResNet：Deep Residual Learning for Image Recognition

Deep Residual Learning for Image Recognition

0 摘要

1. 提出了残差学习框架，简化深度网络训练
2. 显示定义与输入有关的残差函数，重新配置层
3. 残差网络更易优化，随深度增加获得精确度
4. ImageNet上的152层深度残差网络比VGG深８倍，但是复杂性更低
5. 效果很好，ILSVRC-2015冠军

1 引言

背景/问题提出

深度网络融合浅层/中层/高层提取到的特征进行分类，而且是以端到端训练的方式，特征等级随网络叠加变得丰富。

网络深度至关重要。

“学习一个更好的网络是否和堆叠更多的层一样容易？”，过深的网络会有以下问题：

• 梯度消失（弥散）/梯度爆炸问题：初始化正则化、中间层正则化策略来解决。

• 退化问题（正确率饱和后急剧下降，不是过拟合引起的）：层更多（简单的堆叠），训练误差反而更高

  

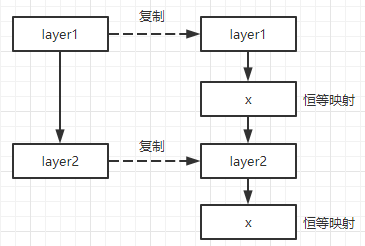
从 浅层模型 构造 深层模型 的方案：添加层时恒等映射，其他层直接拷贝。

这种构造深层模型方法训练误差不比浅层大（增加的层起到的作用是恒等映射），但是也不能找到等优或更优解（或者不能在规定时间内找到）。拟合一个恒等映射代价大效果差

深度残差网络，期望几个堆叠层拟合一个残差函数$F$，而不是原本存在的函数$H$

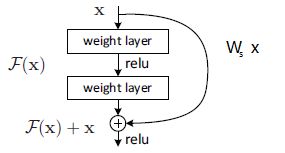
假设映射函数$H(x)$是我们最终期望的获得的，堆叠的非线性层去拟合$F(x)=H(x)-x$，那么原映射函数变成$H(x)=F(x)+x$。假设优化残差映射$F(x)$比优化原始映射$H(x)$要容易

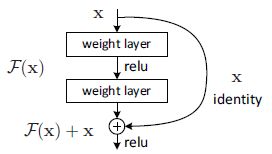
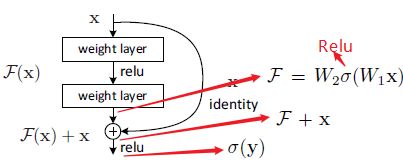
$F(x)+x$可以通过在前向网络捷径连接实现，残差块如下图：

捷径可以跨一层，也可以跨多层；可以是恒等映射，也可以是投影映射，恒等映射既没有引入额外参数，又没有增加计算复杂度

实验说明/贡献

ImageNet上验证

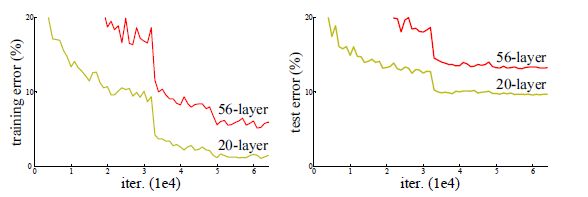
1. 深度残差网络容易优化，但当深度增加时，对应的“普通”网络（简单堆叠层）显示出更高的训练误差，深度残差网络却不会
2. 深度残差网络可以通过增加深度提升精度，产生更好结果

CIFAR-10、ILSVRC、COCO等若干数据集和比赛效果都不错，模型不限定在特定的数据集上

2 相关工作

• 残差表示：VLAD、Fisher Vector编码残差向量（两者都是用于图像检索和分类的强大浅层表示）。求解偏微分方程，用分层预处理（依赖于表示两个标度之间的残差矢量的变量）替代多重网格法，收敛速度更快。

• 捷径连接：通过捷径连接实现中间层响应，梯度和传播误差的方法；“起始”层由捷径分支和更深的分支组成；带有门函数的highway network（门与数据相关且有参数）。

3 深度残差学习

3.1 残差学习

令$H(x)$表示为堆叠层拟合表示的映射，$x$表示第一层的输入。假设多非线性层可以逼近相近的复杂函数，它们就能渐近逼近残差函数$H(x)-x$，令$F(x)=H(x)-x$，那么$H(x)=F(x)+x$。尽管两种形式都应能渐近地逼近所需的函数，但学习的难易程度可能有所不同。

• 多个非线性层拟合$F(x)$，残差映射
• $x$是恒等映射

添加的层如果是拟合恒等映射，那么较深的模型的训练集错误率不会比较浅模型高。但是用多个非线性层去拟合恒等变换更加困难。（举例，如果恒等映射是最优的，那么残差函数接近零就能实现，好于用非线性层拟合一个简单的恒等映射）

*3.2 通过捷径连接实现恒等映射

恒等映射，$x$和$F(x)$维数相等时

$$y=F(x,\{W_i\})+x$$

• $x,y$分别是输入向量和输出向量

• $F(x,\{W_i\})$表示要学习的残差映射，如下图

  

• 这样的形式，没有引入额外参数或计算复杂性。

非恒等映射，$x$和$F(x)$维数不相等时

$$y=F(x,\{W_i\})+W_{s}x$$

• $W_s$是一个线性变换（维数相同情况下，可以认为$W_s$是方阵），用于更改通道数，仅用于匹配尺寸。1x1卷积

  

残差函数$F$说明

• $F$形式灵活，两层/三层是最好的结果，更多的层也是可以的，一层的就是线性变换了，没有什么用
• 尽管为简化起见，上述符号是关于全连接层的，但它们也适用于卷积层。 函数$F（x,\{W_i\}）$可以表示多个卷积层。 在两个功能图上逐个通道执行逐元素加法。

*3.3 网络架构

用于ImageNet的两个模型：

普通网络（34层为例）

baselines

• 3x3卷积
• 对于输出特征维度相同的层，过滤器数目相同
• 当特征映射尺寸减半时，过滤器数目加倍，以保持每层的时间复杂度
• 步长为2的卷积层实现下采样
• 全局平均池化和1000路全连接和softmax层结尾

残差网络（34层，2层残差块）

在上述普通网络的基础上，插入捷径连接，形成相应的残差网络

• 当输入和输出的尺寸相同时，使用恒等映射

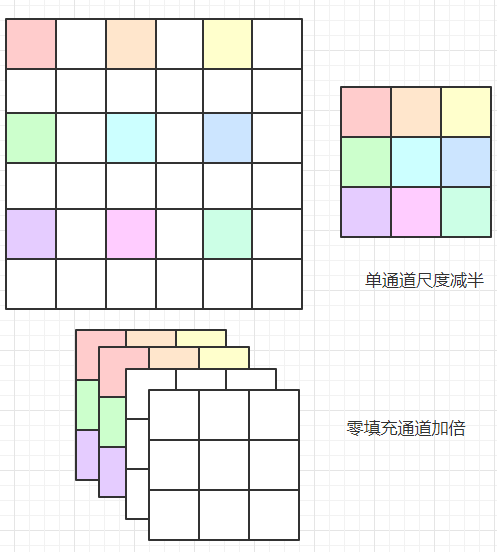
• 当维度增加时（特征通道数变多，单个通道的尺寸减半），有两种选择：

  1. 仍然是恒等映射，用零填充（步长为2）增加的维度

     

  2. 投影映射用于匹配尺寸：按步长为2的1x1的卷积完成通道数目的增加

3.4 实现细节

• 尺寸放缩到[256，480]、图像裁剪、水平翻转、减像素均值、标准颜色增强
• 批归一化
• SGD，mini-batch_size=256，学习率0.1（稳定时除以10），迭代次数：60x10⁴，weight decay=0.0001，momentum=0.9
• 没有使用dropout
• 测试时，五个（左上、右上、左下、右下、中间）、多尺度平均

4 实验

4.1 ImageNet分类任务

普通网络

34层比18层训练集上错误率反而上升了，发生了退化现象，由于BN，不可能是梯度消失引起的。

推测，深层普通网络的收敛速度可能呈指数级降低，这会影响训练误差的降低（未来研究）

*残差网络

基线架构与上述普通网络相同，除了添加了捷径连接实现相应的残差网络。

网络配置

• 捷径连接都使用恒等映射

• 对增加的维度使用零填充

  所以没有额外的参数

观察到的结论：纵向比较，没有退化；横向比较，误差降低；时间比较，收敛更快。

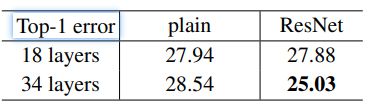
1. 网络没有发生退化，34层ResNet优于18层ResNet。 更重要的是，34层ResNet表现出低得多的训练误差，并且可以推广到验证数据。 这表明在这种情况下可以很好地解决退化问题，并且我们设法从增加的深度中获得准确性的提高。
2. 与普通网络相比，Res34降低了训练误差。 这项比较验证了残差学习在极深系统上的有效性。
3. 18层普通网络比Res18残差网络比较准确，但18层ResNet收敛更快（我感觉差不太多）。 当网“不是太深”时，当前的SGD解算器仍然能够为纯网找到良好的解决方案。 在这种情况下，ResNet通过在早期提供更快的收敛来简化优化。

*捷径连接

捷径连接方案选择，以下三种方案：

1. 增加的维度用零填充，所有捷径连接都是恒等映射
2. 投影捷径用于增加尺寸，其他都是恒等映射
3. 所有连接都是投影捷径

性能上：3 > 2 > 1，但是都差不多。作者用的是第二种。捷径连接方式的不同对解决退化问题并非至关重要。

*深度瓶颈架构（3层残差块）

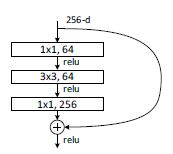
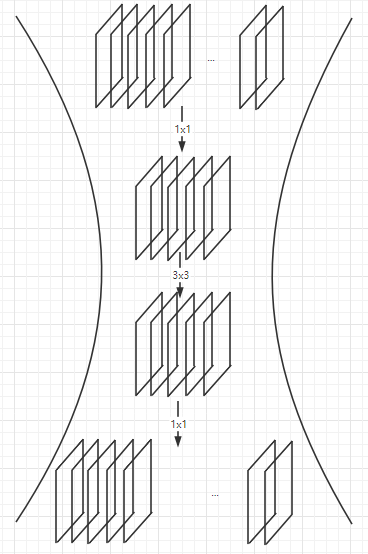
对于每个残差函数$F$，使用3层堆叠。 其中1x1卷积层负责改变通道数（先变小，再变大）不改变尺寸，3x3卷积层更改尺寸。3x3层通道数少，1x1多，所以称为瓶颈。

无参数恒等连接对于瓶颈结构特别重要。 如果将图中的恒等映射替换为投影，则时间复杂度和模型大小增加了一倍。 因此，恒等映射方式可以为瓶颈设计提供更有效的模型。

较浅网络用2层，较深网络用3层

ResNet50

34层基础上，3层瓶颈结构，方案2。

ResNet101、ResNet152

使用更多的3层模块来构建101层和152层ResNet。

尽管深度显着增加，但152层ResNet的复杂度仍低于VGG-16/19网络。

50/101/152层ResNet比34层ResNet准确度高得多。

4.2 CIFAR-10分析

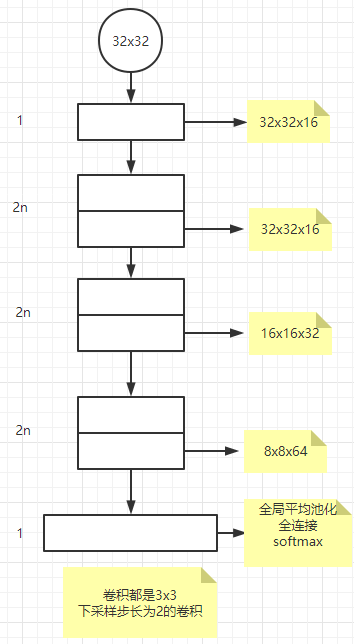
关注点是极端深度网络的行为而不是针对结果，所以使用简单的网络。

都使用恒等映射、零填充方案。

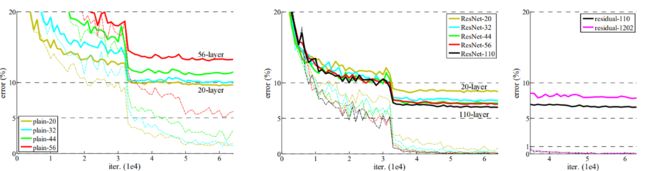
• 普通网络：随深度增加，训练/测试错误率上升
• 残差网络：克服了退化现象
• ResNet110：学习率先是0.01来warm up，当训练错误率低于80%时，学习率变成0.1继续训练

层响应分析

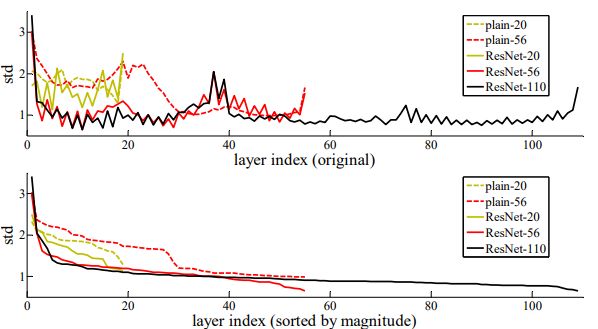
不是很懂这张图含义与意义

• 层响应的标准差，这些响应是BN之后、其他非线性（ReLU /加法）之前每个3x3层的输出的。对于ResNets，分析这些标准差揭示了残差函数的响应强度。
• ResNet的响应通常比普通响应小，说明与非残差函数相比，残差函数通常可能更接近于零。（我觉得只能说明输出更稳定，不能说明趋向于某个值）
• 更深的ResNet具有较小的响应幅度。当有更多层时，ResNets的单个层往往对信号的修改较少。对于更深的层，更可能拟合的是恒等映射，残差函数趋近于0

1000层探索

将n设置为200，形成1202层网络。 结果显示：没有优化困难，该千层网络能够实现训练误差小于0.1%。 其测试误差仍然相当不错。

但是，仍然存在未解决的问题。 尽管1202层网络和110层网络的训练误差相似，但其测试结果却比110层网络的测试结果差。 作者认为这是由于过拟合。 对于该数据集，1202层网络可能会不必要地大。 应用强正则化（例如maxout 或dropout ）以在此数据集上获得最佳结果。 我们不使用maxout / dropout，而只是通过设计通过深度和精简架构强加正则化，而不是将关注点分散到优化困难上。但是，结合更强的正则化可能会改善结果，我们将在以后进行研究。也不能无限叠加网络层。

4.3 目标检测任务

在其他识别任务上泛化性能良好。

基线：PASCAL VOC 2007和2012和COCO。 采用Faster R-CNN作为检测方法。对用ResNet-101替换VGG-16，因为检测实现方式相同，因此收益只能归因于更好的网络。

最值得注意的是，在具有挑战性的COCO数据集上，COCO标准指标（mAP）提高了6.0％，相对提高了28％。 该收益完全归因于所学的表示。

基于深层残差网络，ILSVRC和COCO 2015竞赛的多个赛道上均获得了第一名：ImageNet检测，ImageNet本地化，COCO检测和COCO分割。

5 关键代码

自己仿照Pytorch官方实现写的

class Block(nn.Module): # 跨三层结构
    def __init__(self, input_channel, middle_channel, output_channel, stride=1, down_sample=None):
        super(Block, self).__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channel, middle_channel, kernel_size=1),
            nn.BatchNorm2d(middle_channel),
            nn.ReLU(inplace=True)
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(middle_channel, middle_channel, kernel_size=3, stride=stride, padding=1),
            nn.BatchNorm2d(middle_channel),
            nn.ReLU(inplace=True)
        )
        self.conv3 = nn.Sequential(
            nn.Conv2d(middle_channel, output_channel, kernel_size=1),
            nn.BatchNorm2d(output_channel),
        )
        self.down_sample = down_sample

    def forward(self, x):
        identity = x
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.conv3(x)
        if self.down_sample:
            identity = self.down_sample(identity)
        out = identity + x
        out = F.relu(out, inplace=True)
        return out


class ResNet50(nn.Module):
    def __init__(self, num_class):
        super(ResNet50, self).__init__()
        self.feature = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        )

        def make_layer(input_channel, middle_channel, output_channel, stride, number):
            down_sample = nn.Sequential(
                nn.Conv2d(input_channel, output_channel, 1, stride),
                nn.BatchNorm2d(output_channel)
            )
            layers = [Block(input_channel, middle_channel, output_channel, stride, down_sample)]
            layers.extend([Block(output_channel, middle_channel, output_channel)] for _ in range(1, num_class))
            return nn.Sequential(*layers)

        self.layer1 = make_layer(64, 64, 256, stride=1, number=3)
        self.layer2 = make_layer(256, 128, 512, stride=2, number=4)
        self.layer3 = make_layer(512, 256, 1024, stride=2, number=6)
        self.layer4 = make_layer(1024, 512, 2048, stride=2, number=3)

        self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(2048, num_class)

    def forward(self, x):
        x = self.feature(x)
        x = self.layer1(x)
        x = self.layer2(x)
        x = self.layer3(x)
        x = self.layer4(x)
        x = self.avg_pool(x)
        x = x.reshape(x.size(0), -1)
        x = self.fc(x)
        return x