数据结构(入门篇)
数据结构,简单直白的理解就是指数据的存储方式。
本篇文章代码用java语言写。
我们都知道,数据存储的目的是为了方便后期对数据的再次利用,就像我们使用数据存储{1,2,3,4,5}是为了后期再次利用他们进行相应的数据处理,例如相加取值,但是无缘由的数据存储行为是对存储空间的不负责任。
数据在计算机存储空间的存放不是胡乱存放的,这就要求我们选择一种好的方式来存储数据,而这就是数据结构的核心。
例如大家一直依赖面对的数据存储,都是类似存储1、2、{a,b,c}、"https://blog.csdn.net"等数据,解决方式是用变量或数组对数据进行存储:
int a=1;
int b=2;
char[] ch={'a','b','c'};
String str="https://blog.csdn.net";
但是如果想要存储人物关系数据呢?例如:张三丰有七个弟子宋远桥、俞莲舟、俞岱岩、张松溪、张翠山、殷梨亭、莫声谷,张翠山有儿子(弟子)张无忌,宋远桥有儿子(弟子)宋青书,把整个关系整合一下如下图所示。
对于数据之间有复杂关系的数据,如果还用变量或者数组来存储的话是可以的,例如使用数组方式存储,存储的代码如下。
String[] per={"张三丰","宋远桥","俞莲舟","俞岱岩","张松溪","张翠山","殷梨亭","莫声谷","宋青书","张无忌"};
数据存储是没有问题的,但是存储的数据无法体现数据之间的逻辑关系,后续无法进行数据处理,显然是有问题的。
针对此类数据,数据结构中提供有专门的树结构来存储这类数据。
再比如说,社交软件中的好友推荐功能,根据共同好友的多少来进行好友推荐,如果使用变量或者数组来存储的话是不明智的。
针对此类数据,数据结构提供了图存储结构,专门用于存储这类数据。
通过这些示例我们可以体会出,数据结构并不是简单的存储 1、2、{a,b,c}、"https://blog.csdn.net"这些简单的数据,还会解决很多复杂关系的数据存储问题。
那么现在我们知道了,数据结构不止是进行简单的数据存储,还可以体现出对应的逻辑关系,那么数据结构的数据存储的方式有哪些呢?
数据结构大致包括如下几种存储方式:
·线性表:包括顺序表,链表,栈,队列等
·树结构:包括二叉树,满二叉树,完全二叉树,排序二叉树,平衡二叉树,B树,红黑树等
·图存储结构:包括无向图,有向图,无向网,和有向网等
面对数据结构进行简单讲解。
线性表
线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear list)是数据结构的一种,一个线性表是n个具有相同特性的数据元素的有限序列。
具有1对1的线性关系,首元素和尾元素除外。
顺序表
由于顺序表结构的底层实现就是借助数组实现,所以对于初学者来说,可以将数组当作是顺序表,但并不准确,数据结构是一种存储数据的存储方式,而数组是各种编程语言的一种基本数据类型,并不属于数据结构的范畴。
链表
使用顺序表时,需要提前申请一定大小的存储空间,这块存储空间是连续的,但链表则完全不同,链表存储数据结构是现用现申请的,因此数据的存储位置是相互分离的。链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。 链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。 每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。
栈
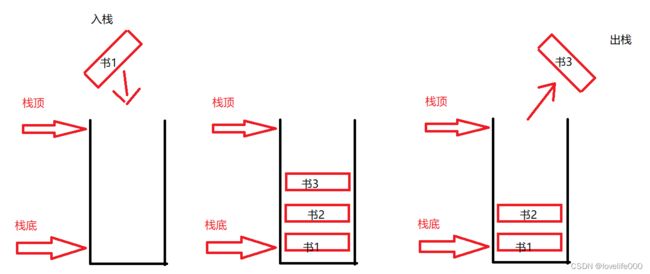
栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。 它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。 栈具有记忆作用,对栈的插入与删除操作中,不需要改变栈底指针。(可以把栈想象成一个装书的箱子,把数据想想成书,最先放箱子里的书需要后放入箱子的书先取出才能取出来,即:先入后出,后入先出)
如图所示,栈结构为一个箱子,有3本书放入箱子的顺序是书1,书2,书3,那么取出书的顺序就是书3,书2,书1。
队列
队列是一种受限制的数据结构,插入操作只能从一端操作,这一端叫做队尾;而移除的话就从另一端操作,这一端叫做队头。举个例子来说,我们将超市结账的队伍称之为一个队列,那么第一个排队的人先结账,结完账就可以离开,那么就表示从这个队列中删除了这个元素,后面排队的人需要等到前一个人结账离开才能结账,新来的人需要到队尾排队。如果没有元素的队列称之为空队,就是说没有人需要排队结账。可以看出,队列的特点是先入先出的一种数据结构。
如上图所示,队列有A、B、C、D、E、F五个元素,依次从队尾进入队列,入队顺序为A、B、C、D、E、F,出队的顺序为A、B、C、D、E、F。
树存储结构
树结构适合存储具有“一对多”关系的数据。
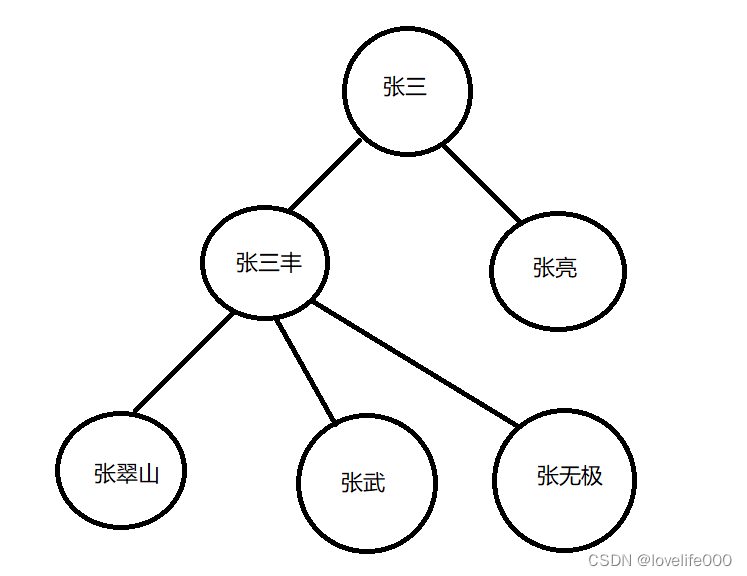
如上图所示,张三有两个孩子,一个叫张三丰,一个叫张亮,而张三丰也有三个孩子,一个叫张翠山,一个叫张武 ,还有一个叫张无极,这就是“一对多”关系,符合一对多的逻辑关系可以使用树结构来进行数据存储。
图存储结构
图存储结构适合存储具有“多对多”关系的数据。
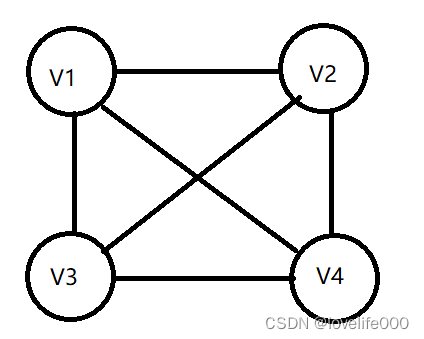
如上图所示,从V1可以到达V2、V3、V4,同样,从V2可以到达V1、V3、V4,从V3可以到达V1、V2、V4,从V4可以到达V1、V2、V3,这就是“多对多”关系,满足这种关系的数据我们可以通过图存储结构来进行数据的存储。
数据的结构
数据的存储方式可以分为线性表、树和图存储方式,而每种存储方式又可以进行更多的细分。那么我们该如何选择存储方式呢?
数据存储结构的选择取决于两个方面,即:数据的逻辑结构和存储结构(又称为物理结构)。
逻辑结构
数据的逻辑结构,简单的理解就是指数据之间的逻辑关系。
如图所示,这是一个家庭成员的关系图,从图中可以看出张三丰和张亮是兄弟,他们的父亲是张三,其中张三丰有三个儿子,分别是张翠山,张武,张无极。
如上述所说,其中父子、兄弟这些关系都是数据间的逻辑关系,假设我们要存储一张家庭成员的表,那么不仅要存储张三,张三丰,张亮等这些数据本身,还需要存储他们之间的关系,两者缺一不可。
一组数据成功存储到计算机的衡量标准是要能将其完整的复原。如上述的家庭成员关系图来说,如果所存储的数据能将此成员关系图彻底复原,则说明数据存储成功。
数据的逻辑关系可以细分为三种:“一对一”,“一对多”,“多对多”:
·“一对一”:类似集合,数组这类的数据{1,2,3,4,5}
·“一对多”:类似上述家庭关系图,家庭成员之间的关系
·“多对多”:图存储结构,之前所述,从V1可以到达V2、V3、V4,同样,从V2可以到达V1、V3、V4,从V3可以到达V1、V2、V4,从V4可以到达V1、V2、V3。对于V1、V2、V3、V4来说,它们之间的关系就是“多对多”的关系
小结
- 线性表用于存储具有“一对一”的逻辑关系的数据
- 树结构用于存储具有“一对多”的逻辑关系的数据
- 图结构用于存储具有“多对多”的逻辑关系的数据
我们可以通过分析数据之间的逻辑关系来选择应该用哪种结构来存储数据,但具体的存储结构还需要通过物理结构来决定。
存储结构(物理结构)
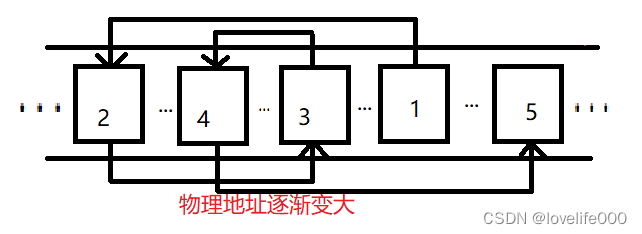
数据的存储结构(物理结构),指的是数据在物理存储空间上选择集中存放还是分散存放。假设要存放10MB的数据,如果集中存储就按照下图图1方式存储,如果分散存储则按照下图图2方式存储。
如果选择集中存储,就使用顺序存储结构;反之,就使用链式存储。至于如何选择,主要取决于存储设备的状态以及数据的用途。
我们知道,集中存储(底层实现使用的是数组)需要使用一大块连续的物理空间,假设要存储大小为 1GB 的数据,若存储设备上没有整块大小超过 1GB 的空间,就无法使用顺序存储,此时就要选择链式存储,因为链式存储是随机存储数据,占用的都是存储设备中比较小的存储空间,因此有一定几率可以存储成功。
并且,数据的用途不同,选择的存储结构也不同。将数据进行集中存储有利于后期对数据进行遍历操作,而分散存储更有利于后期增加或删除数据。因此,如果后期需要对数据进行大量的检索(遍历),就选择集中存储;反之,若后期需要对数据做进一步更新(增加或删除),则选择分散存储。