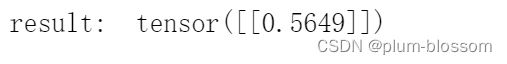NNDL 实验五 前馈神经网络（1）二分类任务

前言

本篇文章是深度学习第五周的实验内容，主要使用pytorch来搭建简单的前馈神经网络，我们一起来学习吧(ง •_•)ง

pytorch实现

导入实验所需要的包：

import numpy as np
import torch
import math
import pandas as pd
import matplotlib.pyplot as plt

4.1 神经元

4.1.1 净活性值

使用pytorch计算一组输入的净活性值z

净活性值z经过一个非线性函数f(·)后，得到神经元的活性值a

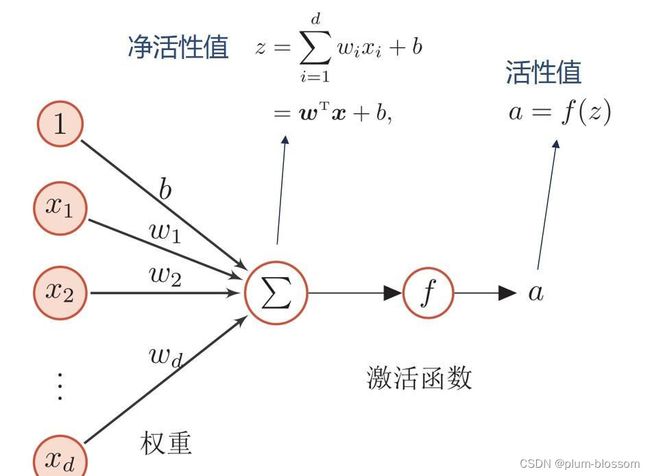
使用pytorch计算一组输入的净活性值:

# 2个特征数为5的样本
X = torch.rand([2, 5])

# 含有5个参数的权重向量
w = torch.rand([5, 1])
# 偏置项
b = torch.rand([1, 1])

# 使用'paddle.matmul'实现矩阵相乘
z = torch.matmul(X, w) + b
print("input X:", X)
print("weight w:", w, "\nbias b:", b)
print("output z:", z)

运行结果：

使用pytorch中相应函数torch.nn.Linear(features_in, features_out, bias=False)实现。

torch.nn.Linear((features_in, features_out, bias=False)函数是一个线性变换函数：

其中，features_in为输入样本的大小，features_out为输出样本的大小，bias默认为true。如果设置bias = false那么该层将不会学习一个加性偏差。

Linear()函数通常用于设置网络中的全连接层。

input = torch.rand([2, 5])
fc = torch.nn.Linear(5, 1, bias=True)
output = fc(input)

print('input: \n', X)
print('fc.weight: \n', fc.weight)
print('fc.bias: \n', fc.bias)
print('output: \n', z)

运行结果：

---

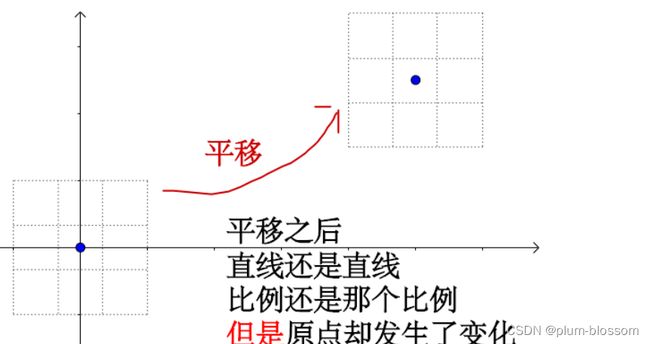
【思考题】加权相加与仿射变换之间有什么区别和联系？

加权和时对输入信息进行线性变换，仿射变换是线性变换+平移。

线性变换有三个特点：

1.变换前是直线，变换后依然是直线；
2.直线比例保持不变
3.变换前是原点，变换后依然是原点

仿射变换有两个特点：

1.变换前是直线，变换后依然是直线；
2.直线比例保持不变

没有了第三点，原点不变，仿射变换后原点是有可能发生变化的。

---

4.1.2 激活函数

激活函数通常为非线性函数，可以增强神经网络的表示能力和学习能力。

常用的激活函数有S型函数和ReLU函数。

4.1.2.1 Sigmoid 型函数

常用的 Sigmoid 型函数有 Logistic 函数和 Tanh 函数。

Logistic函数和Tanh函数的代码实现和可视化如下：

# Logistic函数
def logistic(z):
    return 1.0 / (1.0 + torch.exp(-z))

# Tanh函数
def tanh(z):
    return (torch.exp(z) - torch.exp(-z)) / (torch.exp(z) + torch.exp(-z))

# 在[-10,10]的范围内生成10000个输入值，用于绘制函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z, logistic(z), color='#e4007f', label="Logistic Function")
plt.plot(z, tanh(z), color='#f19ec2', linestyle ='--', label="Tanh Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fw-logistic-tanh.pdf')
plt.show()

运行结果：

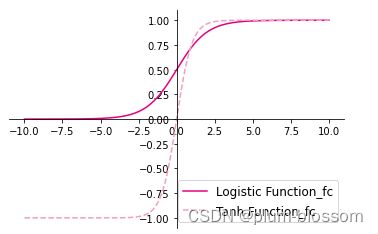
在pytorch中使用torch.nn.functional.sigmoid和torch.nn.functional.tanh实现对张量的Logistic和Tanh计算。

out_1 = torch.nn.functional.sigmoid(z)
out_2 = torch.nn.functional.tanh(z)
plt.plot(z, out_1, color='#e4007f', label="Logistic Function_fc")
plt.plot(z, out_2, color='#f19ec2', linestyle ='--', label="Tanh Function_fc")
ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='lower right', fontsize='large')

plt.savefig('fc-logistic-tanh.pdf')
plt.show()

运行结果：

4.1.2.2 ReLU型函数

常见的ReLU函数有ReLU和带泄露的ReLU（Leaky ReLU）

使用python实现并可视化可视化“ReLU、带泄露的ReLU的函数”

# ReLU
def relu(z):
    return torch.maximum(z, torch.tensor(0.))

# 带泄露的ReLU
def leaky_relu(z, negative_slope=0.1):
    # 当前版本paddle暂不支持直接将bool类型转成int类型，因此调用了paddle的cast函数来进行显式转换
    a1 = (torch.tensor((z > 0), dtype=torch.float32) * z) 
    a2 = (torch.tensor((z <= 0), dtype=torch.float32) * (negative_slope * z))
    return a1 + a2

# 在[-10,10]的范围内生成一系列的输入值，用于绘制relu、leaky_relu的函数曲线
z = torch.linspace(-10, 10, 10000)

plt.figure()
plt.plot(z, relu(z), color="#e4007f", label="ReLU Function")
plt.plot(z, leaky_relu(z), color="#f19ec2", linestyle="--", label="LeakyReLU Function")

ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('fw-relu-leakyrelu.pdf')
plt.show()

运行结果：

在pytorch中使用相应函数torch.nn.functional.relu和torch.nn.functional.leaky_relu并测试。

out_1 = torch.nn.functional.relu(z)
out_2 = torch.nn.functional.leaky_relu(z)
plt.plot(z, out_1, color='#e4007f', label="fc_ReLU Function")
plt.plot(z, out_2, color='#f19ec2', linestyle ='--', label="fc_LeakyReLU Function")

ax = plt.gca() # 获取轴，默认有4个
# 隐藏两个轴，通过把颜色设置成none
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 调整坐标轴位置   
ax.spines['left'].set_position(('data',0))
ax.spines['bottom'].set_position(('data',0))
plt.legend(loc='upper left', fontsize='large')
plt.savefig('cw-relu-leakyrelu.pdf')
plt.show()

运行结果：

---

动手实现《神经网络与深度学习》4.1节中提到的其他激活函数：

Hard-Logistic、Hard-Tanh、ELU、Softplus、Swish等。（选做）

---

4.2 基于前馈神经网络的二分类任务

4.2.1 数据集构建

使用第3.1.1节中构建的二分类数据集：Moon1000数据集，其中训练集640条、验证集160条、测试集200条。该数据集的数据是从两个带噪音的弯月形状数据分布中采样得到，每个样本包含2个特征。

生成数据的函数见上一篇文章

# 采样1000个样本
n_samples = 1000
X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0.5)

num_train = 640
num_dev = 160
num_test = 200

X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]

y_train = y_train.reshape([-1,1])
y_dev = y_dev.reshape([-1,1])
y_test = y_test.reshape([-1,1])

运行结果：

4.2.2 模型构建

为了更高效的构建前馈神经网络，我们先定义每一层的算子，然后再通过算子组合构建整个前馈神经网络。

4.2.2.1 线性层算子

权重参数采用默认的随机初始化，偏置采用默认的零初始化。代码实现如下：

# 实现线性层算子
class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.normal, bias_init=torch.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'paddle.standard_normal'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """
        
        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init(mean=0.,std=1.,size=[input_size,output_size])
        # 初始化偏置
        self.params['b'] = bias_init([1,output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        """
        输入：
            - inputs：shape=[N,input_size], N是样本数量
        输出：
            - outputs：预测值，shape=[N,output_size]
        """
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

4.2.2.2 Logistic算子（激活函数）

将Logistic函数实现一个算子，代码实现如下：

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None

    def forward(self, inputs):
        """
        输入：
            - inputs: shape=[N,D]
        输出：
            - outputs：shape=[N,D]
        """
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

4.2.2.3 层的串行组合

实现一个两层的用于二分类任务的前馈神经网络，选用Logistic作为激活函数，可以利用上面实现的线性层和激活函数算子来组装

# 实现一个两层前馈神经网络
class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2
    

实例化一个两层的前馈网络，令其输入层维度为5，隐藏层维度为10，输出层维度为1。
并随机生成一条长度为5的数据输入两层神经网络，观察输出结果。

# 实例化模型
model = Model_MLP_L2(input_size=5, hidden_size=10, output_size=1)
# 随机生成1条长度为5的数据
X = torch.rand([1, 5])
result = model(X)
print ("result: ", result)

运行结果：

4.2.3 损失函数

二分类交叉熵损失函数见第三章

4.2.4 模型优化

神经网络的层数通常比较深，其梯度计算和上一章中的线性分类模型的不同的点在于：

线性模型通常比较简单可以直接计算梯度，而神经网络相当于一个复合函数，需要利用链式法则进行反向传播来计算梯度。

4.2.4.1 反向传播算法

第1步是前向计算，可以利用算子的forward()方法来实现；
第2步是反向计算梯度，可以利用算子的backward()方法来实现；
第3步中的计算参数梯度也放到backward()中实现，更新参数放到另外的优化器中专门进行。

4.2.4.2 损失函数

二分类交叉熵损失函数

实现损失函数的backward()

# 实现交叉熵损失函数
class BinaryCrossEntropyLoss(Op):
    def __init__(self, model):
        self.predicts = None
        self.labels = None
        self.num = None

        self.model = model

    def __call__(self, predicts, labels):
        return self.forward(predicts, labels)

    def forward(self, predicts, labels):
        """
        输入：
            - predicts：预测值，shape=[N, 1]，N为样本数量
            - labels：真实标签，shape=[N, 1]
        输出：
            - 损失值：shape=[1]
        """
        self.predicts = predicts
        self.labels = labels
        self.num = self.predicts.shape[0]
        loss = -1. / self.num * (torch.matmul(self.labels.t(), torch.log(self.predicts)) 
                + torch.matmul((1-self.labels.t()), torch.log(1-self.predicts)))

        loss = torch.squeeze(loss, 1)
        return loss

    def backward(self):
        # 计算损失函数对模型预测的导数
        loss_grad_predicts = -1.0 * (self.labels / self.predicts - 
                       (1 - self.labels) / (1 - self.predicts)) / self.num
        
        # 梯度反向传播
        self.model.backward(loss_grad_predicts)

4.2.4.3 Logistic算子

为Logistic算子增加反向函数

class Logistic(Op):
    def __init__(self):
        self.inputs = None
        self.outputs = None
        self.params = None

    def forward(self, inputs):
        outputs = 1.0 / (1.0 + torch.exp(-inputs))
        self.outputs = outputs
        return outputs

    def backward(self, grads):
        # 计算Logistic激活函数对输入的导数
        outputs_grad_inputs = torch.multiply(self.outputs, (1.0 - self.outputs))
        return torch.multiply(grads,outputs_grad_inputs)

4.2.4.4 线性层

线性层输入的梯度

计算线性层参数的梯度

class Linear(Op):
    def __init__(self, input_size, output_size, name, weight_init=torch.normal, bias_init=torch.zeros):
        """
        输入：
            - input_size：输入数据维度
            - output_size：输出数据维度
            - name：算子名称
            - weight_init：权重初始化方式，默认使用'paddle.standard_normal'进行标准正态分布初始化
            - bias_init：偏置初始化方式，默认使用全0初始化
        """
        
        self.params = {}
        # 初始化权重
        self.params['W'] = weight_init(mean=0.,std=1.,size=[input_size,output_size])
        # 初始化偏置
        self.params['b'] = bias_init([1,output_size])
        self.inputs = None

        self.name = name

    def forward(self, inputs):
        self.inputs = inputs

        outputs = torch.matmul(self.inputs, self.params['W']) + self.params['b']
        return outputs

    def backward(self, grads):
        """
        输入：
            - grads：损失函数对当前层输出的导数
        输出：
            - 损失函数对当前层输入的导数
        """
        self.grads['W'] = torch.matmul(self.inputs.T, grads)
        self.grads['b'] = torch.sum(grads, axis=0)

        # 线性层输入的梯度
        return torch.matmul(grads, self.params['W'].T)

4.2.4.5 整个网络

实现完整的两层神经网络的前向和反向计算

class Model_MLP_L2(Op):
    def __init__(self, input_size, hidden_size, output_size):
        """
        输入：
            - input_size：输入维度
            - hidden_size：隐藏层神经元数量
            - output_size：输出维度
        """
        self.fc1 = Linear(input_size, hidden_size, name="fc1")
        self.act_fn1 = Logistic()
        self.fc2 = Linear(hidden_size, output_size, name="fc2")
        self.act_fn2 = Logistic()

    def __call__(self, X):
        return self.forward(X)

    def forward(self, X):
        """
        输入：
            - X：shape=[N,input_size], N是样本数量
        输出：
            - a2：预测值，shape=[N,output_size]
        """
        z1 = self.fc1(X)
        a1 = self.act_fn1(z1)
        z2 = self.fc2(a1)
        a2 = self.act_fn2(z2)
        return a2
        
    # 反向计算
    def backward(self, loss_grad_a2):
        loss_grad_z2 = self.act_fn2.backward(loss_grad_a2)
        loss_grad_a1 = self.fc2.backward(loss_grad_z2)
        loss_grad_z1 = self.act_fn1.backward(loss_grad_a1)
        loss_grad_inputs = self.fc1.backward(loss_grad_z1)

4.2.4.6 优化器

在计算好神经网络参数的梯度之后，我们将梯度下降法中参数的更新过程实现在优化器中。

与第3章中实现的梯度下降优化器SimpleBatchGD不同的是，此处的优化器需要遍历每层，对每层的参数分别做更新。

class BatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(BatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        # 参数更新
        for layer in self.model.layers: # 遍历所有层
            if isinstance(layer.params, dict):
                for key in layer.params.keys():
                    layer.params[key] = layer.params[key] - self.init_lr * layer.grads[key]

4.2.5 完善Runner类：RunnerV2_1

支持自定义算子的梯度计算，在训练过程中调用self.loss_fn.backward()从损失函数开始反向计算梯度；
每层的模型保存和加载，将每一层的参数分别进行保存和加载。

class RunnerV2_1(object):
    def __init__(self, model, optimizer, metric, loss_fn, **kwargs):
        self.model = model
        self.optimizer = optimizer
        self.loss_fn = loss_fn
        self.metric = metric

        # 记录训练过程中的评估指标变化情况
        self.train_scores = []
        self.dev_scores = []

        # 记录训练过程中的评价指标变化情况
        self.train_loss = []
        self.dev_loss = []

    def train(self, train_set, dev_set, **kwargs):
        # 传入训练轮数，如果没有传入值则默认为0
        num_epochs = kwargs.get("num_epochs", 0)
        # 传入log打印频率，如果没有传入值则默认为100
        log_epochs = kwargs.get("log_epochs", 100)

        # 传入模型保存路径
        save_dir = kwargs.get("save_dir", None)

        # 记录全局最优指标
        best_score = 0
        # 进行num_epochs轮训练
        for epoch in range(num_epochs):
            X, y = train_set
            # 获取模型预测
            logits = self.model(X)
            # 计算交叉熵损失
            trn_loss = self.loss_fn(logits, y)  # return a tensor

            self.train_loss.append(trn_loss.item())
            # 计算评估指标
            trn_score = self.metric(logits, y).item()
            self.train_scores.append(trn_score)

            self.loss_fn.backward()

            # 参数更新
            self.optimizer.step()

            dev_score, dev_loss = self.evaluate(dev_set)
            # 如果当前指标为最优指标，保存该模型
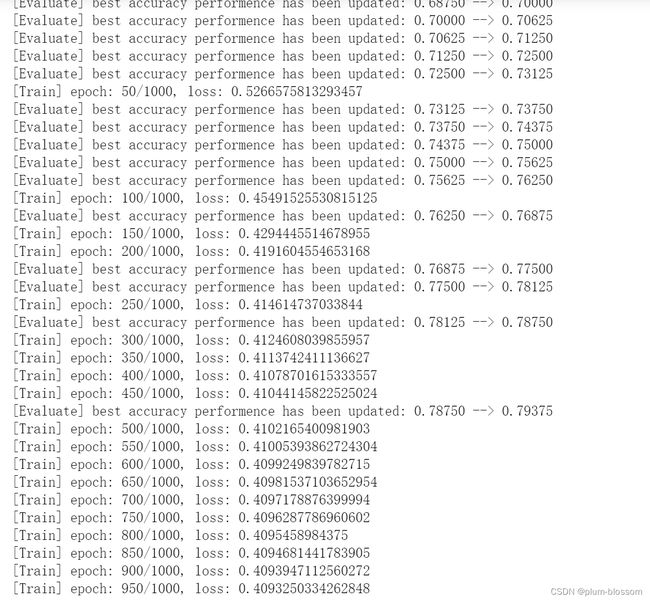
            if dev_score > best_score:
                print(f"[Evaluate] best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
                best_score = dev_score
                if save_dir:
                    self.save_model(save_dir)

            if log_epochs and epoch % log_epochs == 0:
                print(f"[Train] epoch: {epoch}/{num_epochs}, loss: {trn_loss.item()}")

    def evaluate(self, data_set):
        X, y = data_set
        # 计算模型输出
        logits = self.model(X)
        # 计算损失函数
        loss = self.loss_fn(logits, y).item()
        self.dev_loss.append(loss)
        # 计算评估指标
        score = self.metric(logits, y).item()
        self.dev_scores.append(score)
        return score, loss

    def predict(self, X):
        return self.model(X)

    def save_model(self, save_dir):
        # 对模型每层参数分别进行保存，保存文件名称与该层名称相同
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
               torch.save(layer.params, os.path.join(save_dir, layer.name+".pdparams"))

    def load_model(self, model_dir):
        # 获取所有层参数名称和保存路径之间的对应关系
        model_file_names = os.listdir(model_dir)
        name_file_dict = {}
        for file_name in model_file_names:
            name = file_name.replace(".pdparams", "")
            name_file_dict[name] = os.path.join(model_dir, file_name)

        # 加载每层参数
        for layer in self.model.layers:  # 遍历所有层
            if isinstance(layer.params, dict):
                name = layer.name
                file_path = name_file_dict[name]
                layer.params = torch.load(file_path)

4.2.6 模型训练

使用训练集和验证集进行模型训练，共训练2000个epoch。评价指标为accuracy。

epoch_num = 1000

model_saved_dir = 'model'

# 输入层维度为2
input_size = 2
# 隐藏层维度为5
hidden_size = 5
# 输出层维度为1
output_size = 1

# 定义网络
model = Model_MLP_L2(input_size=input_size, hidden_size=hidden_size, output_size=output_size)

# 损失函数
loss_fn = BinaryCrossEntropyLoss(model)

# 优化器
learning_rate = 0.2
optimizer = BatchGD(learning_rate, model)

# 评价方法
metric = accuracy

# 实例化RunnerV2_1类，并传入训练配置
runner = RunnerV2_1(model, optimizer, metric, loss_fn)

runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=epoch_num, log_epochs=50, save_dir=model_saved_dir)

运行结果：

模型训练效果的可视化：

# 打印训练集和验证集的损失
plt.figure()
plt.plot(range(epoch_num), runner.train_loss, color="#e4007f", label="Train loss")
plt.plot(range(epoch_num), runner.dev_loss, color="#f19ec2", linestyle='--', label="Dev loss")
plt.xlabel("epoch", fontsize='large')
plt.ylabel("loss", fontsize='large')
plt.legend(fontsize='x-large')
plt.show()
#加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

4.2.7 性能评价

使用测试集对训练中的最优模型进行评价，观察模型的评价指标。

# 加载训练好的模型
runner.load_model(model_saved_dir)
# 在测试集上对模型进行评价
score, loss = runner.evaluate([X_test, y_test])

print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))

运行结果：

import math

# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-math.pi, math.pi, 200), torch.linspace(-math.pi, math.pi, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], axis=1)

# 预测对应类别
y = runner.predict(x)
y = torch.squeeze(torch.as_tensor((y>=0.5),dtype=torch.float32),dim=-1)

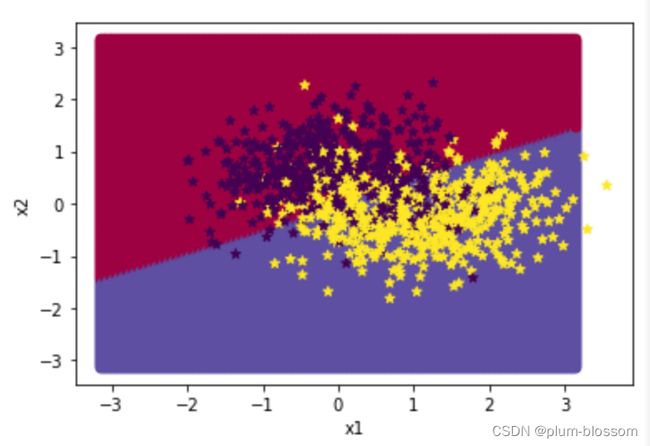
# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)

plt.scatter(X_train[:, 0].tolist(), X_train[:, 1].tolist(), marker='*', c=torch.squeeze(y_train,axis=-1).tolist())
plt.scatter(X_dev[:, 0].tolist(), X_dev[:, 1].tolist(), marker='*', c=torch.squeeze(y_dev,axis=-1).tolist())
plt.scatter(X_test[:, 0].tolist(), X_test[:, 1].tolist(), marker='*', c=torch.squeeze(y_test,axis=-1).tolist())

---

【思考题】对比
3.1 基于Logistic回归的二分类任务
4.2 基于前馈神经网络的二分类任务
谈谈自己的看法：

Logistic回归典型的二值分类器，用来处理两类分类问题，当然，也可以用来处理多类问题，但要转换为One-vs-All或者是One-vs-One问题,Logistic回归并不能很好的区分开复杂的数据集。

Logistic Regression的结构图示：

和前面的Logistic回归相比，神经网络因为有了激活函数的存在，成了一个非线性分类模型，所以神经网络的分类更复杂。

他们的损失函数都使用了交叉熵损失函数。

---

修正

因为torch.normal()在加入高斯噪声的时候sigma设置的过于大，这会使得原本弯月数据集样本点过于分散，失去了数据集原本的特征。

所以将noise设置为0：

X, y = make_moons(n_samples=n_samples, shuffle=True, noise=0)

运行结果：

将噪声设置为0.1可视化如下：

将噪声设置为0.15可视化如下：

noise=0.1训练前馈神经网络的运行结果：


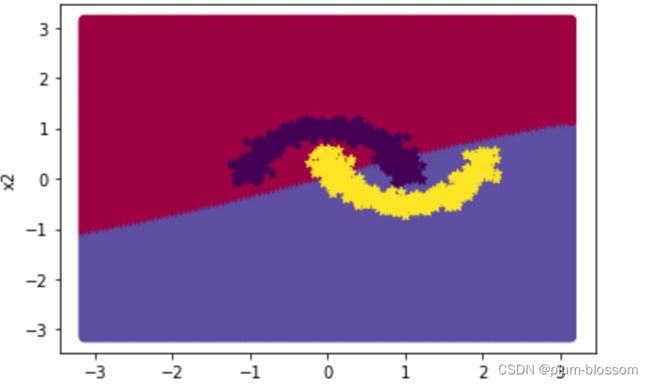
noise=0.15训练前馈神经网络的运行结果：

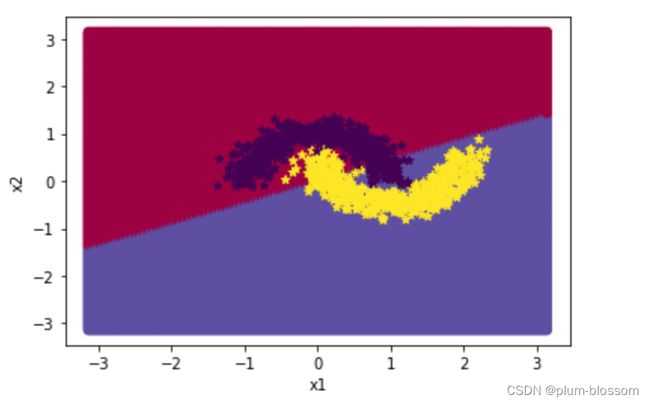
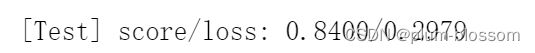
总结

本次实验搭建了一个两层的前馈神经网络，搭建的网络比较简单，训练比较简单的数据集效果还是不错的，并且学习了加权求和与仿射变换的区别，总结了一下Logistic回归模型与前馈神经网络的异同。

参考博客：

从Logistic回归到神经网络

NNDL 实验五 前馈神经网络（1）二分类任务