【opengl】OpenGL中三维物体显示在二维屏幕上显示的变换过程
转自：http://blog.sina.com.cn/s/blog_957b9fdb0100zesv.html
为了说明在三维物体到二维图象之间，需要经过什么样的变换，我们引入了相机（Camera）模拟的方式，假定用相机来拍摄这个世界，那么在相机的取景器中，就存在人眼和现实世界之间的一个变换过程。
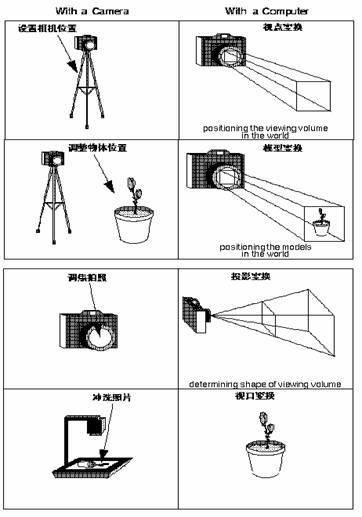
第一步：视点变换（如同拍照的时候设置相机的位置）
在拍照的时候，我们首先要将相机置于三角架上，让它对准三维场景。在OpenGL中调整视点的位置就像是是要放置相机一样，我们称之为视点变换（Viewing Transformation）。
视点变换确定了场景中物体的视点（即相机）的位置和方向，让相机对准要拍摄的物体。缺省时，相机（即视点）定位在世界坐标系的原点，（注意：初始时世界坐标系和当前绘图坐标系位于相同的位置）；相机的初始方向都指向Z负轴。
初始情况下，相机和物体都位于世界坐标系的原点，即相机（视点）与物体是重叠的。试想一下，在用相机拍摄物体时，我们可以保持物体的位置不动，而将相机移离物体，这就相当于视点变换。
视点变换函数gluLookAt()： OpenGL实用库提供了gluLookAt()函数，该函数有三个变量，分别定义了视点的位置、相机瞄准方向的参考点以及相机的向上方向。该函数的原型为：
该函数定义了视点矩阵，并用该矩阵乘以当前矩阵。eyex,eyey,eyez定义了视点的位置；centerx、centery和centerz变量指定了参考点的位置，该点通常为相机所瞄准的场景中心轴线上的点；upx、upy、upz变量指定了向上向量的方向。
使用这个函数之后，只设定好了视点（相机）的位置了。
第二步：模型变换（如同拍照时调整三维物体的位置）
在拍照时，我们也可以保持相机的固定位置，将物体移离相机以将三维物体摆放在场景中的适当位置。在OpenGL中，对物体的显示位置方向的设置就与之类似，我们称之为模型变换（Modeling Transformation）。而显示位置与当前的绘图坐标系密切相关，因为物体总是在当前的绘图坐标系中进行绘制的，因此实际上模型变换可以说就是对当前绘图坐标系位置的变换，这一变换是在世界坐标系下进行的。
设置物体位置涉及到即对模型进行旋转、平移和缩放。缺省时，物体模型（即绘图坐标系）的中心定位在世界坐标系的中心处。OpenGL在这个坐标系中，有如下三个函数来实现模型变换。
1、模型平移
该函数用指定的x,y,z值沿着（世界坐标系的）x轴、y轴、z轴移动绘图坐标系（也即是按照相同的量值平移物体）。
2、模型旋转
该函数中第一个变量angle制定模型旋转的角度，单位为度，后三个变量表示以世界坐标系下的原点（0,0,0）到点(x,y,z)的连线为轴线逆时针旋转绘图坐标系。例如，glRotatef(45.0,0.0,0.0,1.0)的结果是绕z轴旋转45度。
3、模型缩放
该函数可以对物体沿着x,y,z轴分别进行放大缩小。函数中的三个参数分别是x、y、z轴方向的比例变换因子。缺省时都为1.0，即物体没变化。程序中物体Y轴比例为2.0，其余都为1.0，就是说将立方体变成长方体。
注意：通常，视点转换操作在模型转换操作之前发出，以便模型转换先对物体发生作用。场景中物体的顶点经过模型转换之后移动到所希望的位置，然后再对场景进行视点定位等操作。模型转换和视点转换共同构成模型视景矩阵。
第三步：投影变换（就如同拍照中的选镜头并调焦距）
在相机和物体都放好后，我们要选择相机镜头并调焦拍照，使三维物体投影在二维胶片上。与之类似，OpenGL中把三维模型投影到二维屏幕上的过程，即OpenGL的投影变换（Projection Transformation）。
为了使显示的物体能以合适的位置、大小和方向显示出来，必须要通过投影来降低维数。事实上，投影变换的目的就是定义一个视景体，使得视景体外多余的部分裁剪掉，最终进入图像的只是视景体内的有关部分。投影包括透视投影（Perspective Projection）和正视投影（Orthographic Projection）两种。
1. 透视投影
透视投影符合人们心理习惯，即离视点近的物体大，离视点远的物体小，远到极点即为消失，成为灭点。它的视景体类似于一个顶部和底部都被进行切割过的棱椎，也就是棱台。这个投影通常用于动画、视觉仿真以及其它许多具有真实性反映的方面。
OpenGL透视投影函数有两个glFrustum()和gluPerspective（）。
（1）函数glFrustum()：
它创建一个透视视景体。其操作是创建一个透视投影矩阵，并且用这个矩阵乘以当前矩阵（三维物体的各个顶点坐标组成的矩阵）。这个函数的参数只定义近裁剪平面的左下角点和右上角点的三维空间坐标，即（left，bottom，-near）和（right，top，-near）；最后一个参数far是远裁剪平面的Z负值，其左下角点和右上角点空间坐标由函数根据透视投影原理自动生成。near和far表示离视点的远近，它们总为正值。该函数形成的视景体如图三所示。
（2）透视函数gluPerspective（）是：
它也创建一个对称透视视景体，但它的参数定义于前面的不同，参数fovy定义视野在X-Z平面的角度，范围是[0.0, 180.0]；参数aspect是投影平面宽度与高度的比率；参数zNear和Far分别是远近裁剪面沿Z负轴到视点的距离，它们总为正值。
以上两个函数缺省时，视点都在原点，视线沿Z轴指向负方向。
2.正射投影
正射投影，又叫平行投影。这种投影的视景体是一个矩形的平行管道，也就是一个长方体，如图五所示。正射投影的最大一个特点是无论物体距离相机多远，投影后的物体大小尺寸不变。这种投影通常用在建筑蓝图绘制和计算机辅助设计等方面，这些行业要求投影后的物体尺寸及相互间的角度不变，以便施工或制造时物体比例大小正确。
OpenGL正射投影函数也有两个， glOrtho（）和gluOrtho2D（） （1）glOrtho（）：
它创建一个平行视景体。实际上这个函数的操作是创建一个正射投影矩阵，并且用这个矩阵乘以当前矩阵。其中近裁剪平面是一个矩形，矩形左下角点三维空间坐标是（left，bottom，-near），右上角点是（right，top，-near）；远裁剪平面也是一个矩形，左下角点空间坐标是（left，bottom，-far），右上角点是（right，top，-far）。所有的near和far值同时为正或同时为负。如果没有其他变换，正射投影的方向平行于Z轴，且视点朝向Z负轴。这意味着物体在视点前面时far和near都为负值，物体在视点后面时far和near都为正值。
（2）gluOrtho2D（）：
它是一个特殊的正射投影函数，主要用于二维图像到二维屏幕上的投影。它的near和far缺省值分别为-1.0和1.0，所有二维物体的Z坐标都为0.0。因此它的裁剪面是一个左下角点为（left，bottom）、右上角点为（right，top）的矩形。
第四步：视口变换（即着拍照过程中的冲洗底片）
我们知道，冲洗底片就决定二维相片的大小，是2寸是5寸还是10寸。它相当与OpenGL中的视口变换（Viewport Transformation），即在屏幕窗口内可以定义一个矩形，称为视口（Viewport），规定屏幕上场景的范围和尺寸，类似于照片的画布。视景体投影后的图形就在视口内显示，类似于拍摄的图像在画布上显示。
在计算机图形学中，视口变换就是将经过几何变换、投影变换和裁剪变换后的物体显示于屏幕窗口内指定的区域内，这个区域通常为矩形，称为视口。
OpenGL中视口变换的相关函数是：
这个函数定义一个视口。函数参数(x, y)是视口在屏幕窗口坐标系中的左下角点坐标，参数width和height分别是视口的宽度和高度。缺省时，参数值即(0, 0, winWidth, winHeight) 指的是屏幕窗口的实际尺寸大小。所有这些值都是以象素为单位，全为整型数。
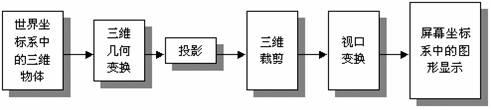
通过上面的几个步骤，一个三维空间里的物体就可以用相应的二维平面物体绘制表示了，也就能在二维的电脑屏幕上正确显示了。总的来说，三维物体的显示过程如下：
|
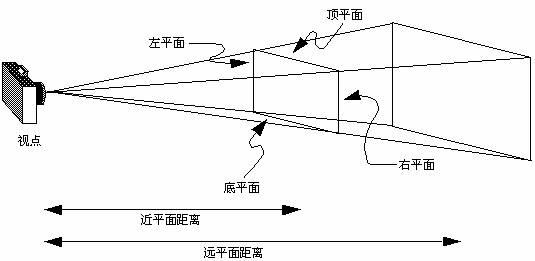图三、透视投影视景体
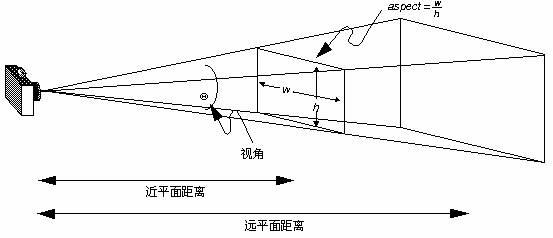图四、透视投影视景体
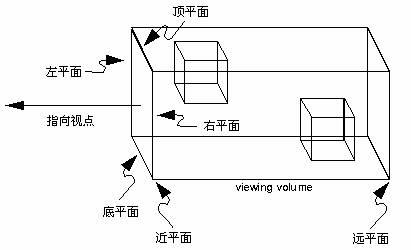图五、正射投影视景体