强化学习：（四）Q-learning, DQN, DDQN是什么？

一、Q-learning

强化学习的一个episode：

强化学习的最终目标：当我处于$s_t$状态，我应该采取从长远来看最好的动作$a_t$

如何实现这个目标？如果$s_t$​状态下，每个可选动作的评分是已知的，我只需要选最高分的动作；但实际上评分是未知的，我需要对它进行估计。

动作评分的定义

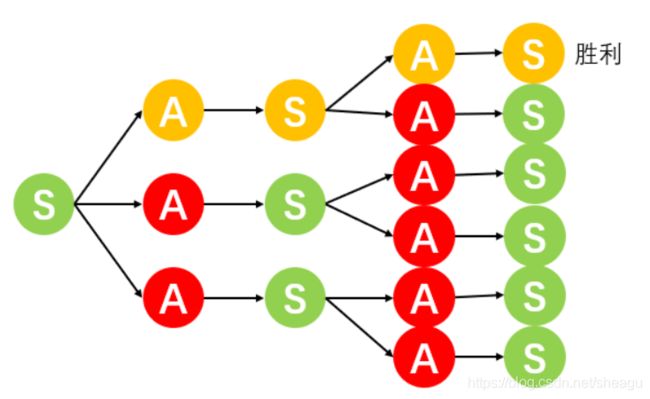
从动态规划的角度来看，如果某个动作可以导向胜利的状态，那么这个动作就得分最高；如果某个动作虽然不能直接胜利，但可以间接导向最容易取胜的状态，那么这个动作就是当前可选动作中得分最高的。如图，橙色的通道是最优通道。

因此，评估一个动作的好坏要看他的长远利益。如何衡量长远的利益？对于每个$(s_t,a_t)$组合，都给出一个奖励$r_t$，那么某个$(s_t,a_t)$​组合的回报定义为：
$$U_t=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+...=\sum _{i=t}^{\infty }{\gamma }^{i-t}{r}_i(1)$$
考虑不确定性：每个$(s_t,a_t)$和下一个$s_t$之间有一个转移概率矩阵，并不是一一对应的，所以，对$a_t$的价值衡量不能直接用$U_t$，要对它求期望。动作价值函数定义为：
$$Q_{\pi }(s_t,a_t)=E[U_t|s_t,a_t,\pi ]=E[\sum _{i=t}^{\infty }{\gamma }^{i-t}{r}_i|s_t,a_t,\pi ](2)$$
我们要做的就是对这个$Q_{\pi }(s_t,a_t)$​​​​进行逼近。怎么逼近呢？

对$U_t$，可以把它写成：
$$U_t=\sum _{i=t}^{\infty }{\gamma }^{i-t}{r}_i=r_t+\gamma (\sum _{i=t+1}^{\infty }{\gamma }^{i-t-1}{r}_i)=r_t+\gamma U_{t+1}(3)$$
因此
$$Q_{\pi }(s_t,a_t)=E[r_t+\gamma U_{t+1}|s_t,a_t,\pi ](4)$$
用神经网络$Q_{\pi }(s_t,a_t,w_t)$​​来逼近$Q_{\pi }(s_t,a_t)$​：​​
$$Q_{\pi }(s_t,a_t,w_t)\approx Q_{\pi }(s_t,a_t)(5)$$
$Q_{\pi }(s_t,a_t,w_t)$的初值是随机给的，通过迭代调整它的权重参数，来使它不断逼近。训练的时候，首先，在$s_t$​​状态，随机指定每个$a_t$​​的动作价值函数$Q_{\pi }(s_t,a_t,w_t)$​​，然后选择目前最好的$a_t$​​（显然是瞎选）。走一步，来到$s_{t+1}$​​，此时我们得到了$r_t$​​，利用这个$r_t$​就可以优化(5)的$Q_{\pi }(s_t,a_t,w_t)$​​​​了：
$$Q_{\pi }(s_t,a_t,w_t)=r_t+\gamma E[U_{t+1}|s_{t+1},a_{t+1},\pi ](6)$$
这个式子之所以能这么写，是因为已经来到了t+1时刻，$r_t$​​已经知道了，而一旦做出动作选择，$(s_{t+1},a_{t+1})$​​也是可以知道的，未知的部分只有$U_{t+1}$​​了，所以它保留了期望的形式。

用(6)得到的$Q_{\pi }(s_t,a_t,w_t)$​​是比(5)的$Q_{\pi }(s_t,a_t,w_t)$​​更准确的，我们称其为TD target，它表示利用已知信息得到的对$Q_{\pi }(s_t,a_t)$​​​​​最准确的估计值：
$$\begin{gathered} y_t^Q=Q_{\pi }(s_t,a_t,w_t) \\ =r_t+\gamma Q_{\pi }(s_{t+1},a_{t+1},w_t) \\ =r_t+\gamma \underset{a}{\max }{Q}_{\pi }(s_{t+1},a,w_t)(6) \end{gathered}$$
由于这里的$y_t^Q$​是已知的对$Q_{\pi }(s_t,a_t)$​的最好的估计，它与上一时刻的估计值$Q_{\pi }(s_t,a_t,w_t)$​​是有差距的，我们就是利用这个差距来优化网络参数。定义loss函数为：
$$L_t=\frac{1}{2}(Q_{\pi }(s_t,a_t,w_t)-y_t^Q{)}^2(7)$$
然后对参数w做梯度下降：
KaTeX parse error: Undefined control sequence: \grad at position 105: …i(s_t,a_t,w_t))\̲g̲r̲a̲d̲_{w_t}Q_\pi(s_t…
让t逐渐增大，直到走完一个episode，那么此时的$y_t^Q$就是对$Q_{\pi }(s_t,a_t)$最好的估计了。但是没走完之前，$y_t^Q$也是在不断优化的，所以可能不需要走完也能得到很精确的对$Q_{\pi }(s_t,a_t)$的估计。可以肯定的是，走完一个episode，沿途经过的所有$Q_{\pi }(s_t,a_t)$都会被更新，但由于从每个状态都只出去了一次，尝试了一个$a_t$，而放弃了其他的，所以每个$Q_{\pi }(s_t,a_t)$都是片面的，而多走几个episode，就可以探索更多的路径，得到更全面的$Q_{\pi }(s_t,a_t)$值。对于已经经过的$(s_t,a_t)$，可以列出Q-Table记录它们的价值，以便下个episode再面临$s_t$的时候，可以选择最好的$a_t$。而下个episode已经知道了一部分$Q_{\pi }(s_t,a_t)$，但还有未知的动作可能带来更大的收益，这就是”探索-利用“的平衡。

Q-Table	a1	a2
s1	q(s1,a1)	q(s1,a2)
s2	q(s2,a1)	q(s2,a2)
s3	q(s3,a1)	q(s3,a2)

二、Deep Q Networks

DQN是 a multi-layered neural network，在Q-learning的基础上增加了target network和experience replay。

target network与在线网络几乎相同，只不过参数不是随时更新的，而是每隔τ步更新一次并保持。DQN用的target表示：
$$y_t^{DQN}=r_t+\gamma \underset{a}{\max }{Q}_{\pi }(s_{t+1},a,w_t^{-})(9)$$
跟$y_t^Q$比起来只有参数$w_t^{-}$不同。

experience replay是指，观测到的状态转移会被存储一段时间，并从这个存储库中均匀采样，以更新网络。

target network和experience replay都显著提高了算法的性能。

三、double Q-learning

在Q-learning和DQN中，”选择下一步动作时使用的评价函数的参数“与”评价所有备选动作时使用的评价函数的参数“是相同的，也就是说，我根据现有的对备选动作的打分值，选出一个最好的，然后我再评估当前的动作价值，依然得到一个很高的分数。这样做存在的问题是，我可能会高估某个动作的分数，而我一旦高估他，我在选动作的时候就会选它，下次打分的时候依然高估，导致一旦出现”高估“就会影响我后面的状态轨迹。

为了避免这种影响，设置两套参数，把”打分“和”选动作“的过程分开。

为了便于对比，先把Q-learning的(6)写成：
$$\begin{gathered} y_t^Q=r_t+\gamma \underset{a}{\max }{Q}_{\pi }(s_{t+1},a,w_t) \\ =r_t+\gamma Q_{\pi }(s_{t+1},\underset{a}{\max }{Q}_{\pi }(s_{t+1},a,w_t),w_t)(10) \end{gathered}$$
也就是说，选动作的时候用的是里面的$w_t$，给选出来的动作再次打分的时候用的是外面的$w_t$。DQN于其类似，只不过是间断性地更新$w_t$。​

而double Q-learning中，target写成：
$$y_t^{DoubleQ}=r_t+\gamma Q_{\pi }(s_{t+1},\underset{a}{\max }{Q}_{\pi }(s_{t+1},a,w_t),w_t^{\prime })$$
也就是说，选动作的时候用的是里面的$w_t$，它是在线的参数；给选出来的动作再次打分的时候用的是外面的$w_t^{\prime }$。每次更新的时候，更新的是$w_t$，如果想更新$w_t^{\prime }$，需要交换$w_t$和$w_t^{\prime }$的地位。

选动作的时候用的是里面的$w_t$，它是在线的参数；给选出来的动作再次打分的时候用的是外面的$w_t^{\prime }$。每次更新的时候，更新的是$w_t$，如果想更新$w_t^{\prime }$，需要交换$w_t$和$w_t^{\prime }$的地位。

形象的理解：某选秀节目分两组评委，第一组给选手打分并选出小组冠军，然后第二组评委再给他重新打分，这个分数作为选手的分数被记录。两组评委过一段时间交换一次。

参考资料

[1] 深度强化学习（全）
[2] 【强化学习】Q-Learning算法详解
[3] H. Van Hasselt, A. Guez, and D. Silver, “Deep reinforcement learning with double q-learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 30, no. 1, 2016.