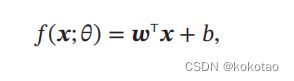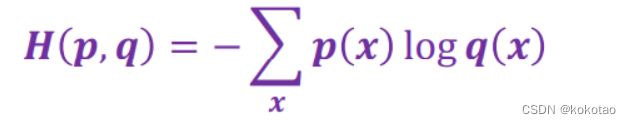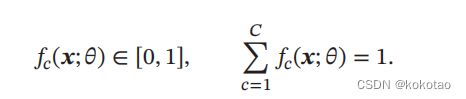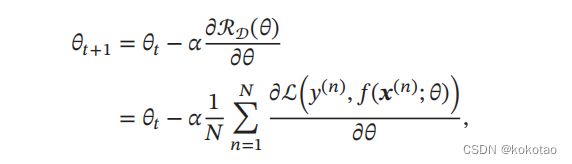神经网络与深度学习（nndl）——2 机器学习概述

机器学习概述

机器学习（ML）定义：就是让计算机从数据中进行自动学习，从而得到某种知识（或规律）早期称为模式识别（PR）

2.1基本概念

样本、特征、标签、模型、学习算法等概念
特征又称为属性（如水果的颜色、大小、产地、品牌、形状等）
标签：是我们需要进行预测的，可以是连续值（如水果的甜度、水分、成熟度的综合打分），也可以是离散的（如好、坏这类标签）
完成标记的标签和特征的东西可以看成一个样本或示例。
数据集（语料库）：样本的集合
特征向量:表示刚刚所列的所有特征构成的向量，每一维表示一个特征，标签通常用标量y表示。
先假设训练集D由N个样本组成（每个样本都是独立同分布的)独立从相同的数据分布中抽取即为

得到训练集D，我们用计算机在函数集合里F={f1(x),f2(x),…}中计算寻找到一个“最优解”的函数f*（x）来近似每个样本的特征向量x和标签y之间的真实映射;
故而函数y*=f*(x）{y*为标签值}/标签的条件概率为p(y|x)=fy*(x).
为了“计算”或“寻找”这个“最优解”要进行学习算法（学习器Learner）来完成，(本章只作概述)
根据提取的特征，使用得到的F*(x)来预测好坏。为了评价的公正性，我们还是独立同分布地抽取另一组为测试集 ′，计算预测结果的准确率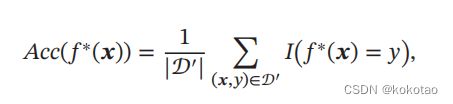
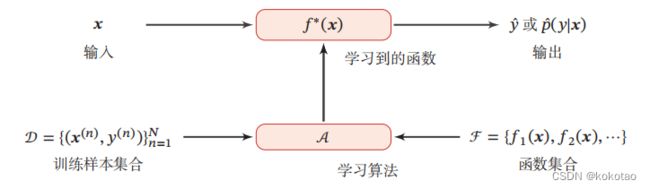
下图是机器学习系统过程图：

对一个预测任务，输入特征向量为 ，输
出标签为，我们选择一个函数集合ℱ，通过学习算法和一组训练样本，从ℱ中学习到函数∗()．这样对新的输入，就可以用函数∗()进行预测．

2.2机器学习三要素

机器学习方法可以粗略地分为三个基本要素：模型、学习准则、优化算法
一，模型：

要确定其输入空间 和输出空间．不同机器学习任务的主要区别在于输出空间不同．在二分类问题中 = {+1, −1}，在 分类问题中 = {1, 2, ⋯ , }，而在回归问题中 = ℝ．

来假设一个函数集合ℱ，称为假设空间（Hypothesis Space），
然后通过观测其在训练集 上的特性，从中选择一个理想的假设（Hypothesis） ∗ ∈ ℱ．
假设空间ℱ 通常为一个参数化的函数族
ℱ = {(; )| ∈ ℝ},

其中(; )是参数为 的函数，也称为模型.

线性模型：在线性模型中的假设空间为一个参数化的线性函数族（family of functions）为：

参数 包含了权重向量和偏置b

非线性模型；

广义非线性模型中能写成多个非线性基函数()的线性组合

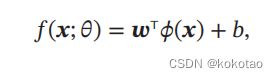
中() = [1(), 2(), ⋯ , ()]T 为 个非线性基函数组成的向量，权值向量W，偏置b；

学习准则：

我们知道训练集D独立同分布样本组成；每个样本都是在X与Y联合空间中拥有着一种未知分布独立随机产生的，但这种未知分布必须是固定的（不会随时间变化而变化）。
一个好的模型 (, ∗) 应该在所有 (, ) 的可能取值上都与真实映射函数
= ()一致，即
|(, ∗) − | < , ∀(, ) ∈ × Y
在这里只是一个很模糊的函数，要借助损失函数来量化其中的差异；

损失函数

损失函数是一个非负实数函数，用来量化模型预测和真实标签之间的差异．

有以下几种损失函数：

1 0-1 损失函数

该函数能最直观的反应模型在训练集上的错误率；

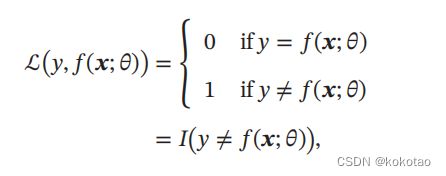
其缺点：是在数学上观察：该函数不连续且导数为0，不好优化，而连续可微的函数数学性质比0-1 损失函数好许多。

2 平方损失函数

该函数多用于预测标签y为实数值；其定义：ℒ(, (; )) = 12( − (; ))2.

缺点：不适用分类问题

3 交叉熵损失函数

给定两个概率分布p和q，通过q来表示p的交叉熵为

交叉熵刻画的是两个概率分布之间的距离， p代表正确答案， q代表的是预测值， 交叉熵越小，两个概率的分布约接近

用于分类问题，设有样本标签签 ∈ {1, ⋯ , } 为离散的类别模型 (; ) ∈ [0,
1]的输出为类别标签的条件概率分布 数学表达：( = |; ) = (; ),且满足：

标签的真实分布和模型预测分布(; )在交叉熵表示为：

2 Hinge 损失函数

通常用于"maximum-margin"的分类任务中，如支持向量机
数学表达式为：

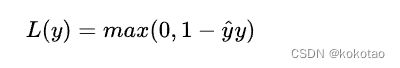
其中y拔表示预测输出，通常都是软结果（就是说输出不是0，1这种，可能是0.87。）， y表示正确的类别。
有关Hinge 损失函数详解参照这位同学的博客

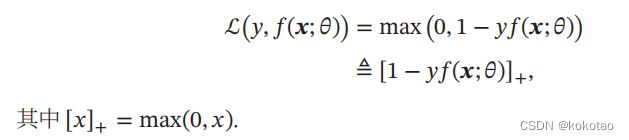
风险最小化准则

一个模型要做到好应该考虑最小的期望错误，上节中我们不知真实的函数分布 和数据存在，从而无法计算期望风险R；在给定的训练集
D={((), ())}=1，计算其经验错误也就是D 的平均损失

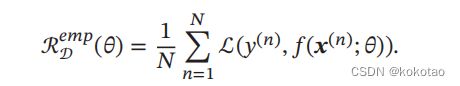
在此过程中找到一组参数使得经验风险最小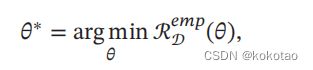
故为经验风险最小化（ERM）准则；

过拟合

在模型中，模型过于复杂，在训练集上面的拟合效果非常好 甚至可以达到损失为0 但是在测试集的拟合效果很不好；
在本节理解：经验风险无限到达期望风险,训练集D无限趋于无穷，但我们是无法获取无穷多的训练样本，在样本的子数据项往往会有一些偏差错误数据（噪声），不是100%真实分布，从中我们可以发现ERM准则会导致模型在该训练集中错误率极低而未知错误会被放大，这样就会过拟合；

欠拟合

模型过于简单 在训练集和测试集的拟合的效果都不好
过拟合，欠拟合，示例例

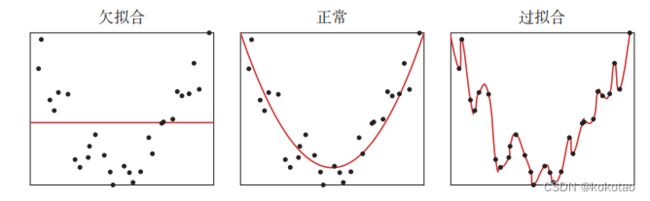
在机器学习中是一个从有限、高维、有噪声的数据中获取一般规律的泛化问题。

梯度下降法

在机器学习中，最简单、常用的优化算法就是梯度下降法
，即首先初始化参
数0，然后按下面的迭代公式来计算训练集 上风险函数的最小值

其中 为第 次迭代时的参数值，为搜索步长．在机器学习中，一般称为学习
率

在进行优化算法中，可以通过提前停止策略来防止过拟合的发生