基于神经网络算法的函数寻优和工程优化
文章目录
- 一、理论基础
-
- 1、神经网络算法
-
- (1)生成初始种群
- (2)权重矩阵
- (3)偏置算子
- (4)激活函数算子
- 2、NNA算法流程图
- 二、仿真实验与结果分析
-
- 1、函数优化
- 2、工程优化
- 三、参考文献
一、理论基础
1、神经网络算法
文献[1]的研究以生物神经系统和人工神经网络为灵感,提出了一种求解复杂优化问题的元启发式优化算法——神经网络算法(Neural network algorithm, NNA),它是基于人工神经网络(Artificial neural networks, ANNs)的独特结构而发展起来的。
(1)生成初始种群
为了解决优化问题,需要将决策变量的值表示为一个数组。在解释NNA过程之前,应该先介绍一下用来描述这种算法的关键术语。每个个体或代理,一个包含每个优化变量的值的集合,被称为“模式解”(例如,在GA中,这个数组被称为“染色体”)。在 D D D维优化问题中,模式解是 1 × D 1\times D 1×D的数组,表示NNA中的输入数据。这个数组的定义如下: P a t t e r n S o l u t i o n = [ x 1 , x 2 , ⋯ , x D ] (1) PatternSolution=[x_1,x_2,\cdots,x_D]\tag{1} PatternSolution=[x1,x2,⋯,xD](1)实际上,模式解的种群对应于人工神经网络中的输入数据。为了启动优化算法,生成一个尺寸为 N p o p × D N_{pop}\times D Npop×D的模式解矩阵候选者。因此,在问题的上下限之间随机生成的矩阵 X X X如下所示(行和列分别是种群数量( N p o p N_{pop} Npop和维度数目( D D D)): P o p u l a t i o n o f P a t t e r n S o l u t i o n s = X = [ x 1 1 x 2 1 x 3 1 ⋯ x D 1 x 1 2 x 2 2 x 3 2 ⋯ x D 2 ⋮ ⋮ ⋮ ⋮ ⋮ x 1 N p o p x 2 N p o p x 3 N p o p ⋯ x D N p o p ] (2) Population\,\,of\,\,Pattern\,\,Solutions=X=\begin{bmatrix} x_1^1 & x_2^1 & x_3^1 & \cdots & x_D^1 \\[2ex]x_1^2 & x_2^2 & x_3^2 & \cdots &x_D^2\\[2ex]\vdots & \vdots & \vdots & \vdots & \vdots \\[2ex] x_1^{N_{pop}} & x_2^{N_{pop}} & x_3^{N_{pop}} & \cdots & x_D^{N_{pop}}\end{bmatrix}\tag{2} PopulationofPatternSolutions=X=⎣ ⎡x11x12⋮x1Npopx21x22⋮x2Npopx31x32⋮x3Npop⋯⋯⋮⋯xD1xD2⋮xDNpop⎦ ⎤(2)每个决策变量值 ( x 1 , x 2 , ⋯ , x D ) (x_1, x_2,\cdots,x_D) (x1,x2,⋯,xD)都可以表示为浮点数(即实数),也可以定义为一组离散变量。模式解的代价是通过对对应模式解的代价函数(适应度函数)( C C C)进行评估得到的,如下所示: C i = f ( x 1 i , x 2 i , ⋯ , x D i ) (3) C_i=f(x_1^i,x_2^i,\cdots,x_D^i)\tag{3} Ci=f(x1i,x2i,⋯,xDi)(3)其中, f f f是目标函数。带有向量符号的符号被对应为向量值(数组),否则其余的符号和参数被认为是标量值。在计算出所有模式解的代价函数(适应度函数)后,再找出被认为是目标解的最佳模式解(本文中为目标函数值最小的候选解)。
NNA类似于具有 D D D维 N p o p N_{pop} Npop输入数据和只有一个目标数据(响应)的 A N N ANN ANN。在其他模式解中设置目标解( X T a r g e t X^{Target} XTarget)后,必须从权重(权重矩阵)的种群中选择目标权重( W T a r g e t W^{Target} WTarget),即与目标解对应的权重。
(2)权重矩阵
ANN的初始权值为随机数,当迭代次数增加时,会考虑网络的计算误差进行更新。回到NNA,初始权值的定义如下式所示: W ( t ) = [ W 1 , W 2 , ⋯ , W N p o p ] = [ w 1 1 ⋯ w 1 i ⋯ w 1 N p o p w 2 1 ⋯ w 2 i ⋯ w 2 N p o p ⋮ ⋮ ⋮ w N p o p 1 ⋯ w N p o p i ⋯ w N p o p N p o p ] = [ w 11 ⋯ w i 1 ⋯ w N p o p 1 w 12 ⋯ w i 2 ⋯ w N p o p 2 ⋮ ⋮ ⋮ w 1 N p o p ⋯ w i N p o p ⋯ w N p o p N p o p ] (4) W(t)=[W_1,W_2,\cdots,W_{N_{pop}}]\\[2ex]=\begin{bmatrix} w_1^1 &\cdots & w_1^i & \cdots & w_1^{N_{pop}} \\[2ex]w_2^1 & \cdots & w_2^i & \cdots & w_2^{N_{pop}}\\[2ex]\vdots & & \vdots & & \vdots \\[2ex] w_{N_{pop}}^1 & \cdots & w_{N_{pop}}^i & \cdots & w_{N_{pop}}^{N_{pop}}\end{bmatrix}=\begin{bmatrix} w_{11} &\cdots & w_{i1} & \cdots & w_{N_{pop}1} \\[2ex]w_{12} & \cdots & w_{i2} & \cdots & w_{N_{pop}2}\\[2ex]\vdots & & \vdots & & \vdots \\[2ex] w_{1N_{pop}} & \cdots & w_{iN_{pop}} & \cdots & w_{N_{pop}N_{pop}}\end{bmatrix}\tag{4} W(t)=[W1,W2,⋯,WNpop]=⎣ ⎡w11w21⋮wNpop1⋯⋯⋯w1iw2i⋮wNpopi⋯⋯⋯w1Npopw2Npop⋮wNpopNpop⎦ ⎤=⎣ ⎡w11w12⋮w1Npop⋯⋯⋯wi1wi2⋮wiNpop⋯⋯⋯wNpop1wNpop2⋮wNpopNpop⎦ ⎤(4)其中, W W W是一个方阵( N p o p × N p o p N_{pop}\times N_{pop} Npop×Npop),它在迭代过程中均匀地生成0到1之间的随机数, t t t是一个迭代索引。权重的第一个下标与它的模式解相关(例如, w 2 × w_{2\times} w2×与第二个模式解相关),权重的第二个下标与其他模式解共享(例如, w 23 w_{23} w23与第三个模式解共享)。每个模式解都有其对应的权重值,该权重值被用于生成新的候选解。
然而,对于权重值有一个限制。施加的约束是模式解决方案的权重总和,在数学上不应超过1,其定义如下: ∑ j = 1 N p o p w i j ( t ) = 1 , i = 1 , 2 , 3 , ⋯ , N p o p (5) \sum_{j=1}^{N_{pop}}w_{ij}(t)=1,\quad i=1,2,3,\cdots,N_{pop}\tag{5} j=1∑Npopwij(t)=1,i=1,2,3,⋯,Npop(5) w i j ∈ U ( 0 , 1 ) i , j = 1 , 2 , 3 , ⋯ , N p o p (6) w_{ij}\in U(0,1)\quad i,j=1,2,3,\cdots,N_{pop}\tag{6} wij∈U(0,1)i,j=1,2,3,⋯,Npop(6)权重值属于0到1之间均匀分布的随机数(式(6)),其中模式解的和不应超过1(式(5))。对权重值的这种约束的存在是由于控制移动的偏差和生成新的模式解(新个体)。如果没有这个约束,权重值倾向于向特定方向增长(即值大于1),因此,算法会卡在一个局部最优点。有了这个约束,NNA的代理就可以以轻微的偏差(从0到1不等)进行受控运动。在形成权重矩阵( W W W)后,使用以下公式计算新的模式解( X N e w X_{New} XNew),其灵感来自于ANN中使用的权重求和方法: X → j N e w ( t + 1 ) = ∑ i = 1 N p o p w i j ( t ) × X → i ( t ) , j = 1 , 2 , 3 , ⋯ , N p o p (7) \overrightarrow X_j^{New}(t+1)=\sum_{i=1}^{N_{pop}}w_{ij}(t)\times\overrightarrow X_i(t),\quad j=1,2,3,\cdots,N_{pop}\tag{7} XjNew(t+1)=i=1∑Npopwij(t)×Xi(t),j=1,2,3,⋯,Npop(7) X → i ( t + 1 ) = X → i ( t ) + X → i N e w ( t + 1 ) , i = 1 , 2 , 3 , ⋯ , N p o p (8) \overrightarrow X_i(t+1)=\overrightarrow X_i(t)+\overrightarrow X_i^{New}(t+1),\quad i=1,2,3,\cdots,N_{pop}\tag{8} Xi(t+1)=Xi(t)+XiNew(t+1),i=1,2,3,⋯,Npop(8)其中, t t t是当前迭代索引。因此, t + 1 t+1 t+1代新的模式解已使用式(7)和式(8)进行更新。例如,如果我们有6个模式解(即6个神经元,种群大小为6),更新第一个新模式解的计算如下: X → 1 N e w ( t + 1 ) = w 11 X → 1 ( t ) + w 21 X → 2 ( t ) + w 31 X → 3 ( t ) + w 41 X → 4 ( t ) + w 51 X → 5 ( t ) + w 61 X → 6 ( t ) (9) \overrightarrow X_1^{New}(t+1)=w_{11}\overrightarrow X_1(t)+w_{21}\overrightarrow X_2(t)+w_{31}\overrightarrow X_3(t)+w_{41}\overrightarrow X_4(t)+w_{51}\overrightarrow X_5(t)+w_{61}\overrightarrow X_6(t)\tag{9} X1New(t+1)=w11X1(t)+w21X2(t)+w31X3(t)+w41X4(t)+w51X5(t)+w61X6(t)(9)在从以前的模式集合中创建新的模式解决方案之后,基于所谓的“目标权重”的最佳权重值,也应该更新权重矩阵。权重矩阵的更新公式为: W → i U p d a t e d ( t + 1 ) = W → i ( t ) + 2 × r a n d × ( W → T a r g e t ( t ) − W → i ( t ) ) , i = 1 , 2 , 3 , ⋯ , N p o p (10) \overrightarrow W_i^{Updated}(t+1)=\overrightarrow W_i(t)+2\times rand\times\left(\overrightarrow W^{Target}(t)-\overrightarrow W^i(t)\right),\quad i=1,2,3,\cdots,N_{pop}\tag{10} WiUpdated(t+1)=Wi(t)+2×rand×(WTarget(t)−Wi(t)),i=1,2,3,⋯,Npop(10)在优化过程中,权重矩阵应始终满足约束条件(5)和(6)。
(3)偏置算子
偏置算子在神经网络模型的动力学中起着至关重要的作用。由于其作用,偏置算子总是与周围条件(如噪声)有所联系,从而使每个神经元的输出涉及周围条件。在NNA中,偏置算子修改了新的模式解总体( X → i N e w ( t + 1 ) \overrightarrow X_i^{New}(t+1) XiNew(t+1))和更新的权重矩阵( W → i U p d a t e d ( t + 1 ) \overrightarrow W_i^{Updated}(t+1) WiUpdated(t+1))中一定百分比的模式解(充当噪声)。换句话说,NNA中的偏置算子是探索搜索空间(探索过程)的另一种方式,其作用类似于GA中的变异算子。
通常,偏置算子可以防止算法过早收敛(尤其是在早期迭代中),并修改种群中的一些个体。事实上,偏置算子对新的模式解(式(7))和更新的权重矩阵(式(10))起着噪声的作用。为此,图1中给出的伪代码已应用于新模式解决方案和更新的权重矩阵。

从图1可以看出, L B LB LB和 U B UB UB分别是问题的下限和上限。如图1所示, β \beta β是一个修改因子,它决定了应该修改的模式解的百分比。 β \beta β的初始值设置为1(意味着有100%的机会修改种群中的所有个体),其值在每次迭代时都使用如下所示的公式自适应地减小: β ( t + 1 ) = β ( t ) × 0.99 t = 1 , 2 , 3 , ⋯ , Max_Iteration (11) \beta(t+1)=\beta(t)\times0.99\quad t=1,2,3,\cdots,\text{Max\_Iteration}\tag{11} β(t+1)=β(t)×0.99t=1,2,3,⋯,Max_Iteration(11) β ( t + 1 ) = 1 − t Max_Iteration t = 1 , 2 , 3 , ⋯ , Max_Iteration (12) \beta(t+1)=1-\frac{t}{\text{Max\_Iteration}}\quad t=1,2,3,\cdots,\text{Max\_Iteration}\tag{12} β(t+1)=1−Max_Iterationtt=1,2,3,⋯,Max_Iteration(12)式(11)和式(12)或任何递减公式都可用于自适应地减少偏差算子,以允许算法在目标解附近搜索最优解,并避免在最后迭代时模式解发生剧烈变化。
(4)激活函数算子
在NNA中,与ANN不同,激活函数算子将种群中的新模式解从其在搜索空间中的当前位置更新到新位置,以便更新并生成针对目标解的更高质量的解。解决方案的改进是通过将当前的新模式解决方案移近最佳解决方案(目标解决方案)来实现的。因此,下式被定义为拟议方法的激活函数算子(TF),如下所示: X → i ∗ ( t + 1 ) = T F ( X → i ( t + 1 ) ) = X → i ( t + 1 ) + 2 × r a n d × ( X → T a r g e t ( t ) − X → i ( t + 1 ) ) , i = 1 , 2 , 3 , ⋯ , N p o p (13) \overrightarrow X_i^*(t+1)=TF(\overrightarrow X_i(t+1))=\overrightarrow X_i(t+1)+2\times rand\times\left(\overrightarrow X^{Target}(t)-\overrightarrow X_i(t+1)\right),\quad i=1,2,3,\cdots,N_{pop}\tag{13} Xi∗(t+1)=TF(Xi(t+1))=Xi(t+1)+2×rand×(XTarget(t)−Xi(t+1)),i=1,2,3,⋯,Npop(13)使用式(13)可将新模式解( X → i ( t + 1 ) \overrightarrow X_i(t+1) Xi(t+1))从其在搜索空间中的当前位置转移到其更新位置( X → i ∗ ( t + 1 ) \overrightarrow X_i^*(t+1) Xi∗(t+1))。图2详细描述了NNA中偏置和TF算子的流程和协作。

2、NNA算法流程图
二、仿真实验与结果分析
1、函数优化
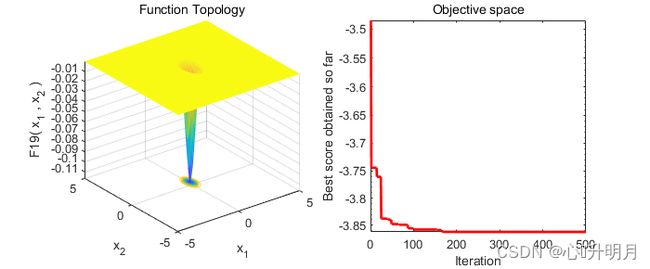
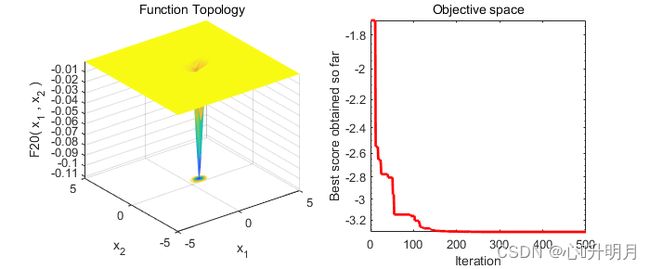
以常用23个测试函数中的F4、F5(单峰函数/100维)、F11、F12(多峰函数/100维)、F19、F20(固定维度多峰函数/3维、6维)为例,实验设置种群规模为30,最大迭代次数为500,结果显示如下:


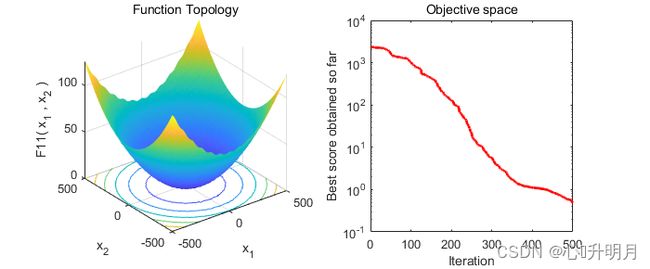

The best solution obtained of F4 by NNA is : 29.01948635 3.275832602 46.6772859 73.15881941 -45.84303073 11.7772628 42.5225719 -65.08052746 28.22422563 77.43975681 -69.19949825 45.41448503 64.01875492 77.43789999 -3.970011608 -0.9816107578 39.98884198 29.43504652 77.44357348 -53.90083647 -4.739079237 -7.080669676 29.99292059 -10.4622763 -38.20057469 76.12779854 -22.36211148 -53.42438277 -22.0921412 -64.23084562 47.51518978 37.21063399 -63.53446003 67.05297006 34.81880044 -70.18396748 -56.55058437 -64.94093858 50.35874772 -70.05897784 -75.58658634 58.60083698 38.21969665 -11.83279857 -34.31470173 -75.91634261 19.815611 77.34302033 -25.97632572 -5.460219306 -0.1583067947 -10.48361199 5.056318552 65.88704595 -34.21639223 66.86046071 -23.57366912 -7.322376358 -19.28317514 -47.7321305 -38.28625405 -74.40789117 41.58648553 -51.58824386 17.61450924 48.21994155 36.73072187 74.90431951 -72.5594918 73.48176344 -26.55219168 73.51153669 77.4441087 -75.2085588 -9.510624877 22.55244028 69.18245823 66.43542226 -74.40637101 76.05382094 75.66188874 -27.57405757 60.48071901 20.57604415 60.41528675 -16.17027647 2.762838591 -75.37129223 17.23405909 77.44089526 48.81065647 -67.60879499 -22.57060611 -2.069146642 -55.97699167 33.82948922 49.59852299 70.36201235 26.71635156 -71.61951259
The best optimal value of F4 found by NNA is : 77.4441087
The best solution obtained of F5 by NNA is : 0.8254891131 0.3979572975 0.4172004694 -0.2763037982 -0.4621556459 0.6728298715 0.2556372308 0.4024433047 -0.1078134689 0.2214859244 0.1625429086 0.1788301089 -0.4917931533 -0.6722597029 0.7943630875 0.8930455452 0.7130444772 0.378713641 0.3988167479 -0.2623735391 -0.07986439317 -0.333879752 -0.06864673089 0.5845989228 0.1600169702 -0.3258192573 -0.4712180764 0.2260270074 0.3245591904 -0.07150986423 0.4185326581 0.2842495107 -0.3917698733 -0.5467476183 0.4447308436 0.2877909279 0.005143357545 -0.05025569812 -0.4239057861 -0.1825215154 -0.3986340965 0.4850689037 0.351082116 -0.08520809038 0.1067116918 0.05954557252 -0.4371475578 0.5283590516 0.4237592392 0.6618542824 0.6546342062 0.2770679466 -0.2417562516 0.2324489969 0.2999644614 0.01583352173 0.08446793527 -0.03585510053 -0.4563439706 0.2915020698 0.1073226973 -0.3860444076 -0.2443848085 0.08420755517 -0.1850792291 -0.08413343085 -0.01306637643 -0.2255352615 -0.344769363 0.1268187946 0.6139028804 0.7026680488 0.648737172 0.3726758673 0.4536272847 0.4332503863 0.5385218924 -0.1578310372 -0.5829872137 0.3598681518 -0.6670465229 0.8120683009 0.823593244 0.549463115 0.03751015048 0.0009536611328 -0.3690828011 0.3127737038 -0.09866927955 0.3482446779 0.5252082339 0.5582709273 -0.08180061593 0.2518889779 -0.5371271432 0.1100882228 -0.07873120715 -2.13109624 5.110992974 26.12014546
The best optimal value of F5 found by NNA is : 1651.261433
The best solution obtained of F11 by NNA is : -0.05420604744 -0.130195681 0.09005907305 0.004900442168 -0.1813750116 -0.3058905101 0.2864052828 -0.3576595392 0.02522367302 0.1459591202 0.05829593282 0.1308964547 0.2360590709 0.8669584783 -1.429132254 0.031131046 0.1540708478 1.042573748 -0.2117134645 0.27600491 -0.03296720673 -1.00842603 -0.6852567807 -0.3771132947 -0.1745915014 0.4080905323 -0.5853034022 0.06970774818 0.03217158578 -0.1900831623 -0.2163683314 0.8479419293 -0.5615093426 -0.3168324294 0.3580050568 0.3391576212 0.5909371354 0.9301343027 -0.565997227 -1.327525262 -0.631852578 0.6451428197 -0.9352180858 -1.134847572 -0.01338922503 0.002262596684 0.9903750183 -0.04597785729 -0.9820099208 0.1941153122 -0.592784682 -1.054868335 0.2811527876 0.2774109285 2.391903599 -1.192110801 -0.006642998873 0.2352784694 -0.3891046991 -0.3624390213 -0.08626141595 -0.7090385286 1.68066896 -0.01194779653 -0.5046548226 0.9982857809 -0.005372835768 0.6734148127 0.1588819268 0.3071467881 0.3533381084 -1.095903095 -0.653136607 -0.166882689 0.4450908855 -1.792064168 -0.3585354936 0.2093063695 -0.9185545085 0.2730042188 0.06133476568 1.200935959 -0.2650682261 0.2007240607 1.35643201 -1.861305754 -0.7385816813 -1.189205703 -1.092195148 -2.28763271 0.9660751799 -0.948326127 0.3133617506 0.3776675444 -0.6244962242 0.8176066705 0.8544328981 -2.065904987 -0.4321817119 0.07937072656
The best optimal value of F11 found by NNA is : 0.483764631
The best solution obtained of F12 by NNA is : -6.358628553 3.221904032 -8.353617287 1.09448149 -5.187505418 -0.127915026 9.047857562 -0.4546526811 9.932789331 6.877001067 -0.6738394137 -0.1383349121 0.06716678455 8.217413703 -4.409926868 6.773109535 3.372448014 9.899557825 2.892469896 -6.087578178 6.956368953 10.18849878 10.17222108 6.534334938 3.586715775 7.633208352 -0.3899005486 -6.112968883 7.016409276 -0.4614511439 -8.2791914 -1.654702118 -8.100922207 -6.141317404 -8.467004936 -9.390428674 -4.472476468 5.987437368 -1.551542658 -0.61802953 -6.602629147 -5.347526298 9.179913079 7.703672492 -1.0715273 -0.7560392042 -1.086118994 -10.11150737 -5.123133673 -8.907533156 -8.707872128 -0.4341305337 3.991396011 -5.001560098 6.256317038 -9.126534402 10.19065072 -0.362400612 8.952762972 -0.1506098955 7.742990087 -5.086798364 -9.028702851 -4.932700589 -7.919874155 -1.137934953 -4.432214252 1.338190751 2.025123485 2.791525763 2.620158041 3.565281024 -1.114578817 7.899571774 -4.776056555 3.508137643 -0.5618906675 -6.126695399 -4.844731606 5.45564297 -1.437788584 5.950349922 -8.929822343 7.269862331 -8.877466739 -1.025470946 5.089456163 -9.142653831 -8.874024463 -5.072655998 3.522733695 -9.477112044 2.966099297 -1.064163633 -4.554398014 -3.6170046 1.252001712 -1.382562004 2.739812058 -1.679636117
The best optimal value of F12 found by NNA is : 18.99530807
The best solution obtained of F19 by NNA is : 0.1146141433 0.5556488599 0.8525469658
The best optimal value of F19 found by NNA is : -3.862782148
The best solution obtained of F20 by NNA is : 0.201707626 0.1467809477 0.4767448444 0.2753423924 0.3116518746 0.657275164
The best optimal value of F20 found by NNA is : -3.321995172
实验结果表明:NAA算法在单峰函数和复杂多峰函数优化上性能较优。
2、工程优化
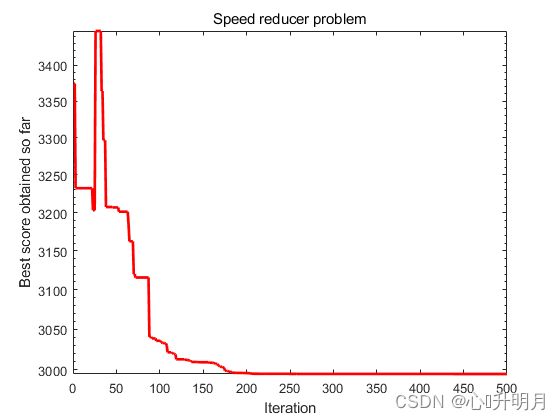
采用直接法对压力容器设计问题、焊接梁设计问题、减速器设计问题、三杆桁架设计问题和轮系设计问题进行优化,实验设置种群规模为30,最大迭代次数为500,结果显示如下:
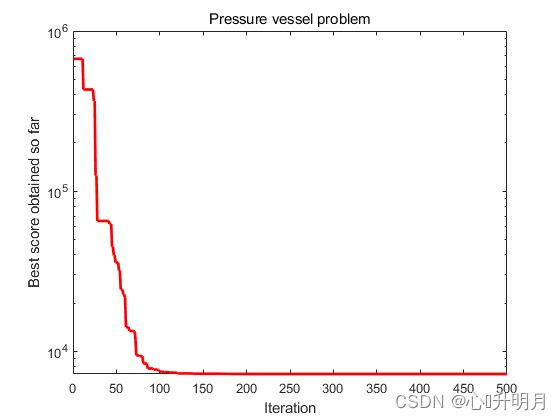


The best solution obtained of Pressure vessel problem by NNA is : 1.238941341 0.6124088413 64.1939037 14.51584513
The best optimal value of Pressure vessel problem found by NNA is : 7231.351296
The best solution obtained of Welded beam problem by NNA is : 0.2057379069 3.470372287 9.036464024 0.20573692
The best optimal value of Welded beam problem found by NNA is : 1.724877147
The best solution obtained of Speed reducer problem by NNA is : 3.499996524 0.7 17 7.300004143 7.715310282 3.350213568 5.286652713
The best optimal value of Speed reducer problem found by NNA is : 2994.468134
The best solution obtained of Three-bar truss problem by NNA is : 0.7900981001 0.4042370314
The best optimal value of Three-bar truss problem found by NNA is : 263.8971929
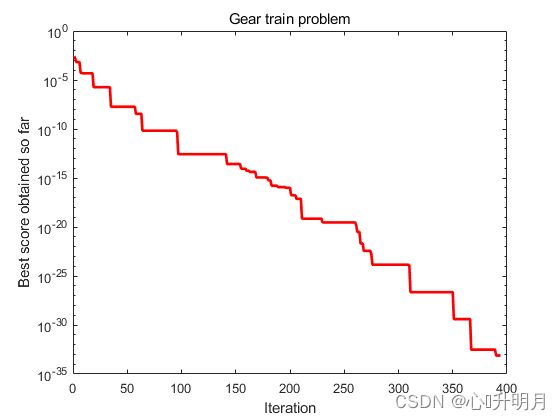
The best solution obtained of Gear train problem by NNA is : 49.93331041 32.69568117 12.58113321 57.09731551
The best optimal value of Gear train problem found by NNA is : 0
实验结果表明:NNA算法在求解复杂工程约束优化问题上具有优异的性能。
三、参考文献
[1] Ali Sadollah, Hassan Sayyaadi, Anupam Yadav. A dynamic metaheuristic optimization model inspired by biological nervous systems: Neural network algorithm[J]. Applied Soft Computing, 2018, 71: 747-782.
