基于正交设计的折射反向学习樽海鞘群算法
文章目录
- 一、理论基础
-
- 1、樽海鞘群算法
- 2、正交反向学习樽海鞘群算法OOSSA
-
- (1)正交反向学习策略
- (2)惯性权重策略
- (3)OOSSA算法
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、樽海鞘群算法
请参考这里。
2、正交反向学习樽海鞘群算法OOSSA
(1)正交反向学习策略
为增强SSA算法跳出局部最优的能力,提出一种正交反向学习策略(Orthogonal lens opposition-based learning, OLOBL),并将其应用到领导者个体上产生新的个体。
将OLOBL策略嵌入SSA算法,优化问题的维度 D D D对应正交试验设计中的因素,个体与折射反向个体即为正交试验设计中的两个水平。构建部分反向解的具体描述过程为:对当前个体和其折射反向个体设计一个2水平 D D D因素的正交试验,产生 M M M个部分折射反向解, M M M按照式(1)进行计算。其中,根据正交试验表产生部分反向解时,若正交表的元素为1,试验解对应维上取当前个体的值;若正交表的元素为2,试验解对应维上取折射反向个体的值。 M = 2 ⌈ log 2 ( D + 1 ) ⌉ (1) M=2^{\lceil\log_2(D+1)\rceil}\tag{1} M=2⌈log2(D+1)⌉(1)根据正交试验特性,正交表中第一行的元素全为1,这就代表第一组试验解即为个体本身,不需要评估。另外 M − 1 M-1 M−1组试验解是当前个体与其反向个体优势维度的结合,即部分折射反向解,需要评估。在使用正交试验设计时,需进行因素分析,找出一组不存在于正交表中的理论最优组合,需要评估。因此,执行一次OLOBL策略需要的函数评估次数为 M M M次。在进化迭代过程中,仅对领导者执行OLOBL策略,并从领导者和其正交折射反向个体中选择较优个体进入下一代,这样可以有效增强算法的全局探索能力,同时减少函数的评价次数,从而改善算法的整体性能。
(2)惯性权重策略
由追随者位置更新模型可知,基本SSA中追随者在保留自身特征的同时学习前一个个体,完成位置更新。其位置更新机制较为单一,一旦领导者陷入局部最优,追随者必然跟随至该局部极值区域。为增强跟随者位置更新机制的灵活性,引入一种非线性递减惯性权重来评价前一个个体对当前追随者的影响程度。新的追随者位置更新公式为: X j i = 1 2 ( X j i + ω X j i − 1 ) (2) X_j^i=\frac12(X_j^i+\omega X_j^{i-1})\tag{2} Xji=21(Xji+ωXji−1)(2) ω = ω max − ( ω max − ω min ) 2 2 + e ( 10 − 0.04 t ) (3) \omega=\omega_{\max}-(\omega_{\max}-\omega_{\min})\frac{2}{2+e^{(10-0.04t)}}\tag{3} ω=ωmax−(ωmax−ωmin)2+e(10−0.04t)2(3)其中, ω \omega ω为本文设计的惯性权重, ω max \omega_{\max} ωmax和 ω min \omega_{\min} ωmin分别为初始惯性权重和最终惯性权重。
(3)OOSSA算法
所提OOSSA算法的实现流程如下:
Step 1:设置算法参数:种群规模 N N N,最大函数评价次数 F max F_{\max} Fmax,搜索维度 D D D,搜索区域上下边界 u b ub ub、 l b lb lb;在搜索空间中随机生成 N N N个樽海鞘个体构成初始种群;
Step 2:计算初始种群的适应度值并排序,首个个体定义为领导者,其余个体为追随者,并将适应值最优个体的位置作为当前食物源;
Step 3:判断樽海鞘个体角色:若为领导者则进入Step 4;若为跟随者则进入Step 5;
Step 4:根据基本SSA公式更新领导者位置,产生候选解1,同时执行OLOBL策略,产生候选解2,根据适应值保留候选解1和候选解2中的较优个体;
Step 5:根据式(2)更新追随者位置;
Step 6:比较食物源和当前最优个体的适应值,取较优者作为新的食物源;
Step 7:若函数评价次数达到最大函数评估次数 F max F_{\max} Fmax,则输出食物源位置,即为最优解;否则,返回Step 3继续迭代。
二、仿真实验与结果分析
将OOSSA与MPA、EO、ArOA(算术优化算法)、AOA(阿基米德优化算法)、MFO和SSA进行对比,以文献[1]中表1的F1、F2、F4、F6、F8、F12(100维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
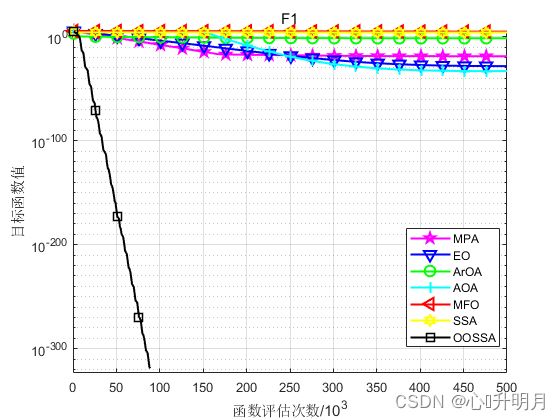
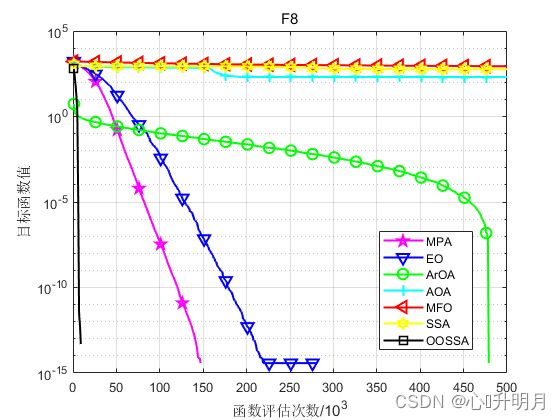
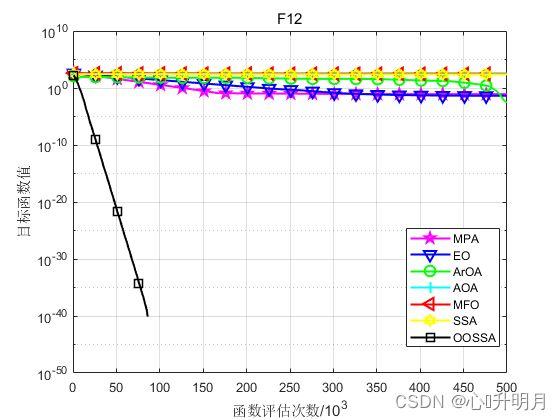
函数:F1
MPA:最差值: 4.8164e-19, 最优值: 1.658e-21, 平均值: 1.648e-19, 标准差: 1.3091e-19, 秩和检验: 1.2118e-12
EO:最差值: 3.4735e-28, 最优值: 4.8975e-31, 平均值: 5.0453e-29, 标准差: 8.7788e-29, 秩和检验: 1.2118e-12
ArOA:最差值: 0.057409, 最优值: 0.012746, 平均值: 0.028131, 标准差: 0.011098, 秩和检验: 1.2118e-12
AOA:最差值: 9.132e-33, 最优值: 4.1882e-55, 平均值: 7.5488e-34, 标准差: 2.2535e-33, 秩和检验: 1.2118e-12
MFO:最差值: 96506.8739, 最优值: 34211.4829, 平均值: 65256.967, 标准差: 14913.2428, 秩和检验: 1.2118e-12
SSA:最差值: 13334.9287, 最优值: 5860.8846, 平均值: 8896.5135, 标准差: 1440.4645, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
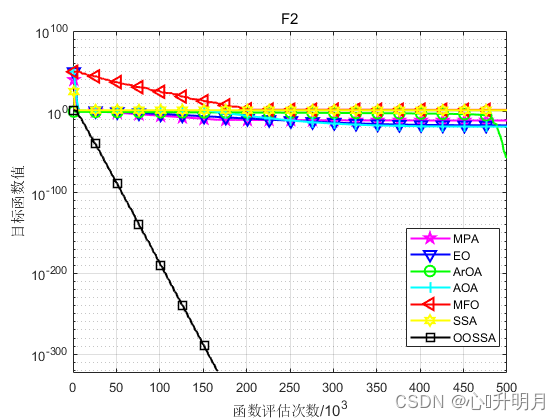
函数:F2
MPA:最差值: 8.9362e-11, 最优值: 1.7804e-12, 平均值: 1.8929e-11, 标准差: 1.8636e-11, 秩和检验: 1.2118e-12
EO:最差值: 7.7114e-17, 最优值: 3.9399e-18, 平均值: 1.8458e-17, 标准差: 1.7231e-17, 秩和检验: 1.2118e-12
ArOA:最差值: 5.7904e-56, 最优值: 5.5101e-125, 平均值: 1.9301e-57, 标准差: 1.0572e-56, 秩和检验: 1.2118e-12
AOA:最差值: 3.8344e-18, 最优值: 1.6073e-31, 平均值: 4.6348e-19, 标准差: 1.1646e-18, 秩和检验: 1.2118e-12
MFO:最差值: 337.7706, 最优值: 149.4393, 平均值: 228.4882, 标准差: 44.7875, 秩和检验: 1.2118e-12
SSA:最差值: 85.6765, 最优值: 60.2626, 平均值: 74.1526, 标准差: 6.8651, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
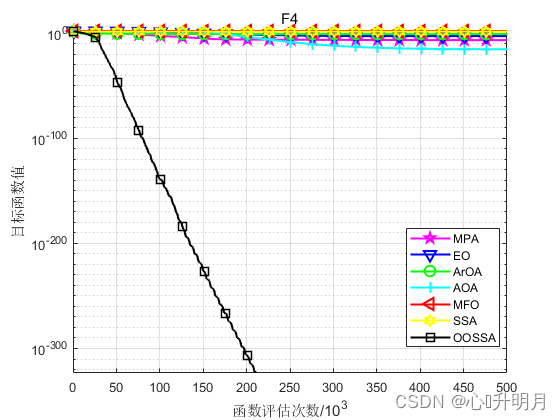
函数:F4
MPA:最差值: 4.0195e-07, 最优值: 5.5016e-08, 平均值: 2.241e-07, 标准差: 9.521e-08, 秩和检验: 1.2118e-12
EO:最差值: 0.012566, 最优值: 8.2393e-05, 平均值: 0.0012423, 标准差: 0.0024912, 秩和检验: 1.2118e-12
ArOA:最差值: 0.11996, 最优值: 0.075144, 平均值: 0.095721, 标准差: 0.01288, 秩和检验: 1.2118e-12
AOA:最差值: 4.2978e-15, 最优值: 4.8099e-26, 平均值: 4.6878e-16, 标准差: 9.8292e-16, 秩和检验: 1.2118e-12
MFO:最差值: 95.735, 最优值: 87.9428, 平均值: 92.969, 标准差: 2.0744, 秩和检验: 1.2118e-12
SSA:最差值: 29.509, 最优值: 20.3161, 平均值: 23.6047, 标准差: 3.0109, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
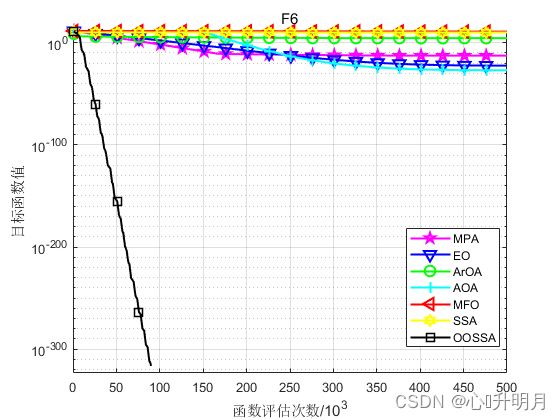
函数:F6
MPA:最差值: 9.9507e-13, 最优值: 1.9879e-15, 平均值: 1.9423e-13, 标准差: 2.2748e-13, 秩和检验: 1.2118e-12
EO:最差值: 1.7555e-22, 最优值: 1.1003e-24, 平均值: 3.5045e-23, 标准差: 4.8872e-23, 秩和检验: 1.2118e-12
ArOA:最差值: 48558.2612, 最优值: 1623.7546, 平均值: 25871.9943, 标准差: 11521.8475, 秩和检验: 1.2118e-12
AOA:最差值: 2.4431e-26, 最优值: 2.8886e-49, 平均值: 1.1318e-27, 标准差: 4.6701e-27, 秩和检验: 1.2118e-12
MFO:最差值: 83566555369.6217, 最优值: 46689149712.7212, 平均值: 63379912575.884, 标准差: 11122753564.7708, 秩和检验: 1.2118e-12
SSA:最差值: 12357828083.4108, 最优值: 5466338481.4231, 平均值: 8361180488.8352, 标准差: 1508537433.0758, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F8
MPA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
EO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
ArOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
AOA:最差值: 730.6309, 最优值: 0, 平均值: 204.0077, 标准差: 318.1009, 秩和检验: 0.0013702
MFO:最差值: 1005.0804, 最优值: 718.323, 平均值: 861.1039, 标准差: 74.8905, 秩和检验: 1.2118e-12
SSA:最差值: 670.806, 最优值: 491.3082, 平均值: 581.9182, 标准差: 41.7575, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F12
MPA:最差值: 0.2558, 最优值: 0.033535, 平均值: 0.083094, 标准差: 0.044831, 秩和检验: 1.2118e-12
EO:最差值: 0.14805, 最优值: 0.011771, 平均值: 0.043449, 标准差: 0.029693, 秩和检验: 1.2118e-12
ArOA:最差值: 0.018557, 最优值: 3.2634e-06, 平均值: 0.0032758, 标准差: 0.0052809, 秩和检验: 1.2118e-12
AOA:最差值: 383.2732, 最优值: 2.5087e-06, 平均值: 366.8532, 标准差: 69.7169, 秩和检验: 1.2118e-12
MFO:最差值: 329.5867, 最优值: 289.2314, 平均值: 307.0269, 标准差: 8.3795, 秩和检验: 1.2118e-12
SSA:最差值: 260.1072, 最优值: 226.7014, 平均值: 242.2641, 标准差: 8.1252, 秩和检验: 1.2118e-12
OOSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
实验结果表明:OOSSA算法在求解精度和收敛速度方面表现出较大优势。
三、参考文献
[1] 王宗山, 丁洪伟, 王杰, 等. 基于正交设计的折射反向学习樽海鞘群算法[J]. 哈尔滨工业大学学报, 2022, 54(11): 122-136.
[2] 周凌云, 丁立新, 马懋德, 等. 一种正交反向学习萤火虫算法[J]. 电子与信息学报, 2019, 41(1): 202-209.
[3] 庞善起, 鹿姗姗. 正交表的构造方法及Matlab实现[J]. 中国卫生统计, 2017, 34(2): 364-367.