[机器学习入门笔记] 3.监督学习集成模型部分
文章目录
- 前言
- 第 11 章 AdaBoost
-
- 11.1 Boosting
- 11.2 AdaBoost算法的原理推导
-
- 11.2.1 AdaBoost基本原理
- 11.2.2 AdaBoost与前向分步算法
- 11.3 AdaBoost算法实现
-
- 11.3.1 基于Numpy的AdaBoost算法实现
- 11.3.2 基于sklearn的AdaBoost实现
- 11.4 小结
- 第 12 章 GBDT
-
- 12.1 从提升树到梯度提升树
- 12.2 GBDT算法的原理推导
- 12.3 GBGT算法实现
-
- 12.3.1 基于Numpy的GBDT算法实现
- 12.3.2 基于sklearn的GBDT实现
- 12.4 小结
- 第 13 章 XGBoost
-
- 13.1 XGBoost 极度梯度提升树
- 13.2 XGBoost原理推导
- 13.3 XGBoost算法实现
-
- 13.3.1 XGBoost实现:基于GBDT的改进
- 13.3.2 基于原生库示例
- 13.4 小结
前言
继 [机器学习入门笔记] 3.监督学习单模型部分,更新了集成学习模型~
第 11 章 AdaBoost
11.1 Boosting
集成学习
将多个弱分类器组成一个强分类器,该强分类器能取所有若分类器之长,达到相对的最优性能。
Boosting是机器学习中一种集成学习框架,Boosting方法在分类问题中,通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。
11.2 AdaBoost算法的原理推导
11.2.1 AdaBoost基本原理
提升方法就是从若学习算法出发,反复学习,得到一系列若分类器(基本分类器),然后组合这些弱分类器,构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布(训练数据的权值分布),针对不同的训练数据分布调用弱学习算法学习的一系列弱分类器。
Boosting方法解决的两个关键
- 训练过程中如何改变训练样本的权重或概率分布
- 如何将弱分类器组合成强分类器
AdaBoost解决关键的方法
- 提高前一轮被弱分类器分类错误的样本的权重,降低分类正确的样本的权重
- 对多个弱分类器进行线性组合,提高分类效果好的弱分类器的权重,降低分类误差率高的弱分类器的权重
给定训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} D={(x1,y1),(x2,y2),...,(xN,yN)},其中 x i ∈ X ⊆ R n x_i∈X \subseteq R^n xi∈X⊆Rn, y i ∈ Y = { − 1 , + 1 } y_i\in Y=\{-1,+1\} yi∈Y={−1,+1},AdaBoost训练算法如下:
- 初始化训练数据样本的权重分布,即为每个训练样本分配一个初始权重:
D 1 = ( w 11 , . . . , w 1 i ) , w 1 i = 1 N , i = 1 , 2 , . . . , N D_1=(w_{11},...,w_{1i}),w_{1i}=\frac{1}{N},\quad i=1,2,...,N D1=(w11,...,w1i),w1i=N1,i=1,2,...,N
-
对于 t = 1 , 2 , . . . , T t=1,2,...,T t=1,2,...,T,分别执行以下步骤。
- 对包含权重分布 D t D_t Dt的训练集进行训练得到弱分类器 G t ( x ) G_t(x) Gt(x)
- 计算 G t ( x ) G_t(x) Gt(x)在当前加权训练集上的分类误差率 ϵ t \epsilon_t ϵt:
ϵ t = P ( G t ( x i ) ≠ y i ) = ∑ i = 1 N w t i I ( G t ( x i ) ≠ y i ) \epsilon_t=P(G_t(x_i)≠y_i)=\sum_{i=1}^{N}{w_{ti}I(G_t(x_i)≠y_i)} ϵt=P(Gt(xi)=yi)=i=1∑NwtiI(Gt(xi)=yi)
- 根据分类误差率 ϵ t \epsilon_t ϵt计算当前弱分类器的权重系数 α t \alpha_t αt:
α t = 1 2 l o g 1 − ϵ t ϵ t \alpha_t=\frac{1}{2}log{\frac{1-\epsilon_t}{\epsilon_t}} αt=21logϵt1−ϵt
- 调整训练集的权重分布:
D t + 1 = ( w t + 1 , 1 , . . . , w t + 1 , i , w t + 1 , N ) w t + 1 , i = w t i Z t e x p ( − α t y i G t ( x i ) ) , 其中 Z t 为归一化因子, Z t = ∑ i = 1 N w t i e x p ( − α t y i G t ( x i ) ) D_{t+1}=(w_{t+1},1,...,w_{t+1,i},w_{t+1,N})\\ w_{t+1,i}=\frac{w_{ti}}{Z_t}exp(-\alpha_ty_iG_t(x_i)),\\ 其中Z_t为归一化因子,Z_t=\sum_{i=1}^{N}{w_{ti}}exp(-\alpha_ty_iG_t(x_i)) Dt+1=(wt+1,1,...,wt+1,i,wt+1,N)wt+1,i=Ztwtiexp(−αtyiGt(xi)),其中Zt为归一化因子,Zt=i=1∑Nwtiexp(−αtyiGt(xi))
-
最后构建弱分类器的线性组合:
f ( x ) = ∑ t = 1 T α t G t ( x ) f(x)=\sum_{t=1}^{T}\alpha_tG_t(x) f(x)=t=1∑TαtGt(x)
最终强分类器可以写为:
G ( x ) = s i g n ( f ( x ) ) = s i g n ( ∑ t = 1 T α t G t ( x ) ) G(x)=sign(f(x))=sign(\sum_{t=1}^{T}\alpha_tG_t(x)) G(x)=sign(f(x))=sign(t=1∑TαtGt(x))
11.2.2 AdaBoost与前向分步算法
从机器学习模型、策略、算法三要素来看,AdaBoost是以加性模型为模型、指数函数为损失函数、前向分步为算法的分类学习算法。
加性模型
模型是由多个基模型求和的形式构造起来的。
考虑加性模型: f ( x ) = ∑ t = 1 T α t b ( x ; γ t ) f(x)=\sum_{t=1}^{T}{\alpha_t}b(x;\gamma_t) f(x)=∑t=1Tαtb(x;γt),其中 b ( x ; γ t ) b(x;\gamma_t) b(x;γt)为基模型, γ t \gamma_t γt为模型参数, α t \alpha_t αt为基模型系数,可知 f ( x ) f(x) f(x)是由 T T T个模型求和的加性模型。
给定训练集和损失函数的条件下,加性模型的目标函数为如下最小化损失函数:
min α t , γ t ∑ i = 1 N L ( y i , ∑ t = 1 T α t b ( x i ; γ t ) ) \min\limits_{\alpha_t,\gamma_t}\sum_{i=1}^{N}{L(y_i,\sum_{t=1}^{T}{\alpha_tb(x_i;\gamma_t)})} αt,γtmini=1∑NL(yi,t=1∑Tαtb(xi;γt))
针对这种较复杂的优化问题采用向前分步算法,其基本思路:针对加性模型的特点,从前往后每次只优化一个基模型的参数,每一步优化叠加之后便可逐步逼近上述目标函数,每一步优化如下:
min α t , γ t ∑ i = 1 N L ( y i , α t b ( x i ; γ t ) ) \min\limits_{\alpha_t,\gamma_t}\sum_{i=1}^{N}{L(y_i,{\alpha_tb(x_i;\gamma_t)})} αt,γtmini=1∑NL(yi,αtb(xi;γt))
给定训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} D={(x1,y1),(x2,y2),...,(xN,yN)},其中 x 1 ∈ X ⊆ R n , y i ∈ Y = − 1 , + 1 x_1∈X\subseteq R^n,y_i\in Y={-1,+1} x1∈X⊆Rn,yi∈Y=−1,+1,利用向前分步算法求解加性模型 f ( x ) = ∑ t = 1 T α t b ( x ; γ t ) f(x)=\sum_{t=1}^{T}{\alpha_t}b(x;\gamma_t) f(x)=∑t=1Tαtb(x;γt)的优化问题的过程如下。
-
初始化模型 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0
-
对于 t = 1 , 2 , . . . , T t=1,2,...,T t=1,2,...,T分别执行以下操作
- 以 α t \alpha_t αt和 γ t \gamma_t γt为优化参数,最小化目标损失函数:
( α t , γ t ) = a r g min α , γ ∑ i = 1 N L ( y i , f t − 1 ( x i ) + α b ( x ; γ t ) ) (\alpha_t,\gamma_t)=arg\min\limits_{\alpha,\gamma}\sum_{i=1}^{N}{L(y_i,f_{t-1}(x_i)+\alpha b(x;\gamma_t))} (αt,γt)=argα,γmini=1∑NL(yi,ft−1(xi)+αb(x;γt))
- 更新加性模型:
f t ( x ) = f t − 1 ( x ) + α t b ( x ; γ t ) f_t(x)=f_{t-1}(x)+\alpha_tb(x;\gamma_t) ft(x)=ft−1(x)+αtb(x;γt)
- 可得到最后加性模型:
f ( x ) = f T ( x ) = ∑ t = 1 T α t b ( x ; γ t ) f(x)=f_T(x)=\sum_{t=1}^{T}{\alpha_tb(x;\gamma_t)} f(x)=fT(x)=t=1∑Tαtb(x;γt)
从向前分步算法的角度理解AdaBoost,可将AdaBoost看作向前分步算法的特例,此时加性模型是以分类器为基模型、以指数函数为损失函数的最优化问题。假设经过 t − 1 t-1 t−1次向前分步迭代后已经得到 f t − 1 ( x ) f_{t-1}(x) ft−1(x),第 t t t次迭代可以得到第 t t t个基模型的权重系数 α t \alpha_t αt、第 t t t个基模型 G t ( x ) G_t(x) Gt(x)和 t t t轮迭代后的加性模型 f t ( x ) f_t(x) ft(x):
f t ( x ) = f t − 1 ( x ) + α t G t ( x ) f_t(x)=f_{t-1}(x)+\alpha_tG_t(x) ft(x)=ft−1(x)+αtGt(x)
优化目标是使 f t ( X ) f_t(X) ft(X)在给定训练集 D D D上的指数损失最小化,有:
( α t , G t ( x ) ) = a r g min α , G ∑ i = 1 N e x p ( − y i ( f t − 1 ( x i ) + α G ( x i ) ) ) ( ∗ ) (\alpha_t,G_t(x))=arg\min\limits_{\alpha,G}\sum_{i=1}^{N}{exp(-y_i(f_{t-1}(x_i)+\alpha G(x_i)))}\quad\quad(*) (αt,Gt(x))=argα,Gmini=1∑Nexp(−yi(ft−1(xi)+αG(xi)))(∗)
求解式 ( ∗ ) (*) (∗)的最小化指数损失即可得到AdaBoost的优化参数。
11.3 AdaBoost算法实现
AdaBoost算法代码编写思路
Numpy:
- 经典版本
- 基分类器
- AdaBoost经典算法流程
- 权重初始化
- 训练弱分类器
- 计算当前分类误差
- 计算弱分类器权重
- 更新训练样本权重
- 定义预测函数
- 数据测试
sklearn:
- ensemble.AdaBoostClassifier
11.3.1 基于Numpy的AdaBoost算法实现
决策树桩分类器
### 定义决策树桩类
### 作为Adaboost弱分类器
class DecisionStump():
def __init__(self):
# 基于划分阈值决定样本分类为1还是-1
self.label = 1
# 特征索引
self.feature_index = None
# 特征划分阈值
self.threshold = None
# 指示分类准确率的值
self.alpha = None
AdaBoost拟合函数
# Adaboost算法拟合过程
def fit(X, y, n_estimators):
'''
输入:
X:训练输入
y:训练输出
n_estimators:基分类器个数
输出:
estimators:包含所有基分类器的列表
'''
m, n = X.shape
# (1) 初始化权重分布为均匀分布 1/N
w = np.full(m, (1/m))
# 处初始化基分类器列表
self.estimators = []
# (2) for m in (1,2,...,M)
for _ in range(self.n_estimators):
# (2.a) 训练一个弱分类器:决策树桩
estimator = DecisionStump()
# 设定一个最小化误差
min_error = float('inf')
# 遍历数据集特征,根据最小分类误差率选择最优划分特征
for i in range(n):
# 获取特征值
values = np.expand_dims(X[:, i], axis=1)
# 特征取值去重
unique_values = np.unique(values)
# 尝试将每一个特征值作为分类阈值
for threshold in unique_values:
p = 1
# 初始化所有预测值为1
pred = np.ones(np.shape(y))
# 小于分类阈值的预测值为-1
pred[X[:, i] < threshold] = -1
# 2.b 计算误差率
error = sum(w[y != pred])
# 如果分类误差大于0.5,则进行正负预测翻转
# 例如 error = 0.6 => (1 - error) = 0.4
if error > 0.5:
error = 1 - error
p = -1
# 一旦获得最小误差则保存相关参数配置
if error < min_error:
estimator.label = p
estimator.threshold = threshold
estimator.feature_index = i
min_error = error
# 2.c 计算基分类器的权重
estimator.alpha = 0.5 * np.log((1.0 - min_error) / (min_error + 1e-9))
# 初始化所有预测值为1
preds = np.ones(np.shape(y))
# 获取所有小于阈值的负类索引
negative_idx = (estimator.label * X[:, estimator.feature_index] < estimator.label * estimator.threshold)
# 将负类设为 '-1'
preds[negative_idx] = -1
# 2.d 更新样本权重
w *= np.exp(-estimator.alpha * y * preds)
w /= np.sum(w)
# 保存该弱分类器
estimators.append(estimator)
定义预测函数
# 定义预测函数
def predict(X,esitmators):
'''
输入:
X:预测输入
estimators:包含所有基分类器的列表
输出:
y_pred:预测输出
'''
m = len(X)
y_pred = np.zeros((m, 1))
# 计算每个弱分类器的预测值
for estimator in self.estimators:
# 初始化所有预测值为1
predictions = np.ones(np.shape(y_pred))
# 获取所有小于阈值的负类索引
negative_idx = (estimator.label * X[:, estimator.feature_index] < estimator.label * estimator.threshold)
# 将负类设为 '-1'
predictions[negative_idx] = -1
# 2.e 对每个弱分类器的预测结果进行加权
y_pred += estimator.alpha * predictions
# 返回最终预测结果
y_pred = np.sign(y_pred).flatten()
return y_pred
AdaBoost算法类
### 定义AdaBoost算法类
class Adaboost:
# 弱分类器个数
def __init__(self, n_estimators=5):
self.n_estimators = n_estimators
# Adaboost拟合算法
def fit(self, X, y):
m, n = X.shape
# (1) 初始化权重分布为均匀分布 1/N
w = np.full(m, (1/m))
# 处初始化基分类器列表
self.estimators = []
# (2) for m in (1,2,...,M)
for _ in range(self.n_estimators):
# (2.a) 训练一个弱分类器:决策树桩
estimator = DecisionStump()
# 设定一个最小化误差
min_error = float('inf')
# 遍历数据集特征,根据最小分类误差率选择最优划分特征
for i in range(n):
# 获取特征值
values = np.expand_dims(X[:, i], axis=1)
# 特征取值去重
unique_values = np.unique(values)
# 尝试将每一个特征值作为分类阈值
for threshold in unique_values:
p = 1
# 初始化所有预测值为1
pred = np.ones(np.shape(y))
# 小于分类阈值的预测值为-1
pred[X[:, i] < threshold] = -1
# 2.b 计算误差率
error = sum(w[y != pred])
# 如果分类误差大于0.5,则进行正负预测翻转
# 例如 error = 0.6 => (1 - error) = 0.4
if error > 0.5:
error = 1 - error
p = -1
# 一旦获得最小误差则保存相关参数配置
if error < min_error:
estimator.label = p
estimator.threshold = threshold
estimator.feature_index = i
min_error = error
# 2.c 计算基分类器的权重
estimator.alpha = 0.5 * np.log((1.0 - min_error) / (min_error + 1e-9))
# 初始化所有预测值为1
preds = np.ones(np.shape(y))
# 获取所有小于阈值的负类索引
negative_idx = (estimator.label * X[:, estimator.feature_index] < estimator.label * estimator.threshold)
# 将负类设为 '-1'
preds[negative_idx] = -1
# 2.d 更新样本权重
w *= np.exp(-estimator.alpha * y * preds)
w /= np.sum(w)
# 保存该弱分类器
self.estimators.append(estimator)
# 定义预测函数
def predict(self, X):
m = len(X)
y_pred = np.zeros((m, 1))
# 计算每个弱分类器的预测值
for estimator in self.estimators:
# 初始化所有预测值为1
predictions = np.ones(np.shape(y_pred))
# 获取所有小于阈值的负类索引
negative_idx = (estimator.label * X[:, estimator.feature_index] < estimator.label * estimator.threshold)
# 将负类设为 '-1'
predictions[negative_idx] = -1
# 2.e 对每个弱分类器的预测结果进行加权
y_pred += estimator.alpha * predictions
# 返回最终预测结果
y_pred = np.sign(y_pred).flatten()
return y_pred
数据测试
# 导入数据划分模块
from sklearn.model_selection import train_test_split
# 导入模拟二分类数据生成模块
from sklearn.datasets.samples_generator import make_blobs
# 导入sklearn准确率计算函数
from sklearn.metrics import accuracy_score
# 生成模拟二分类数据集
X, y = make_blobs(n_samples=150, n_features=2, centers=2,
cluster_std=1.2, random_state=40)
# 将标签转换为1/-1
y_ = y.copy()
y_[y_==0] = -1
y_ = y_.astype(float)
# 训练/测试数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y_,
test_size=0.3, random_state=43)
# 设置颜色参数
colors = {0:'r', 1:'g'}
# 绘制二分类数据集的散点图
plt.scatter(X[:,0], X[:,1], marker='o', c=pd.Series(y).map(colors))
plt.show();
# 创建Adaboost模型实例
clf = Adaboost(n_estimators=5)
# 模型拟合
clf.fit(X_train, y_train)
# 模型预测
y_pred = clf.predict(X_test)
# 计算模型预测准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy of AdaBoost by numpy:", accuracy)
11.3.2 基于sklearn的AdaBoost实现
# 导入sklearn adaboost分类器
from sklearn.ensemble import AdaBoostClassifier
# 创建Adaboost模型实例
clf_ = AdaBoostClassifier(n_estimators=5, random_state=0)
# 模型拟合
clf_.fit(X_train, y_train)
# 模型预测
y_pred_ = clf_.predict(X_test)
# 计算模型预测准确率
accuracy = accuracy_score(y_test, y_pred_)
print("Accuracy of AdaBoost by sklearn:", accuracy)
11.4 小结
- Boosting是一种将多个若分类器组合成强分类器的集成学习算法框架,AdaBoost是一种通过改变训练样本权重来学习多个弱分类器并将其线性组合成强分类器的Boosting算法
- AdaBoost特点是通过迭代每次学习一个弱分类器,在每次迭代的过程中,提高前一轮分类数据错误的权重,降低分类正确数据的权重。最后将弱分类器线性组合成一个强分类器
- 从机器学习三要素,AdaBoost可理解为以加性模型为模型、指数函数为损失函数、前向分步为算法的分类学习算法
第 12 章 GBDT
12.1 从提升树到梯度提升树
提升方法实际采用加法模型(基模型的线性组合)与前向分步算法。以决策树为基模型的提升方法称提升树(boosting tree)。当损失函数为平方损失和指数损失时,前向分步算法的每一步迭代较容易求解,对于一般的损失函数,前向分步算法的每一步迭代并不容易。所以,有研究提出使用损失函数的负梯度在当前模型的值来求解更为一般的提升树模型。这种基于负梯度求解提升树前向分步迭代过程的方法也叫梯度提升树。
12.2 GBDT算法的原理推导
GBDT的全称为梯度提升决策树,其基模型为CART决策树,针对分类问题的基模型为二叉分类树,对应梯度提升模型叫GBDT;针对回归问题的基模型为二叉回归树,对应的梯度提升模型叫GBRT。
[参考解释GBDT:假设某人月薪10k,用一个树模型拟合了6k,发现有4k的损失,然后再用一棵树模型拟合了2k,持续拟合下去,拟合值和目标值之间的残差越来越小。将每一轮迭代看,也就是每一棵树的预测值加起来,就是模型最终预测结果。]
使用多棵决策树组合就是提升树模型,使用梯度下降法对提升树模型进行优化的过程就是梯度提升树模型。
一个提升树模型的数学表达式为:
f M ( x ) = ∑ m = 1 M T ( x ; Θ m ) f_M(x)=\sum_{m=1}^{M}{T(x;\Theta_m)} fM(x)=m=1∑MT(x;Θm)
其中 T ( x ; Θ m ) T(x;\Theta_m) T(x;Θm)为决策树表示的模型, Θ m \Theta_m Θm表示决策树参数, M M M为决策树棵数。
当确定初始提升树模型 f 0 ( x ) = 0 f_0(x)=0 f0(x)=0,第 m m m的模型表示为:
f m ( x ) = f m − 1 ( x ) + T ( x ; Θ m ) f_m(x)=f_{m-1}(x)+T(x;\Theta_m) fm(x)=fm−1(x)+T(x;Θm)
其中 f m − 1 ( x ) f_{m-1}(x) fm−1(x)为当前迭代模型,根据前向分步算法,可以使用经验风险最小化来确定下一个决策树的参数 Θ m \Theta_m Θm
根据加性模型,第0步、第m步和最终模型可以表示为:
在已知 f m ( x ) f_m(x) fm(x)情况下求解下式可以得到当前迭代步的模型参数。
假设回归树的损失函数为平方损失:
L ( y , f ( x ) ) = ( y − f ( x ) ) 2 L(y,f(x))=(y-f(x))^2 L(y,f(x))=(y−f(x))2
对应到GBRT中,损失推导为:
其中,
r = y − f m − 1 ( x ) r=y-f_{m-1}(x) r=y−fm−1(x)
提升树每一次迭代都在拟合一个残差函数。大多数情况下,一般损失函数很难直接优化求解,因而有了基于负梯度求解提升树模型的梯度提升树模型。
梯度提升树以梯度下降的方法,使用损失函数的负梯度在当前模型的值作为回归提升树中残差的近似值:
r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi}=-[\frac{\partial{L(y_i,f(x_i))}}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
因此,综合提升树模型、前向分步算法和梯度提升,给定训练集 D = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } , x i ∈ X , y i ∈ Y ⊆ R n D=\{(x_1,y_1),...,(x_N,y_N)\},x_i\in X,y_i\in Y\subseteq R^n D={(x1,y1),...,(xN,yN)},xi∈X,yi∈Y⊆Rn,GBDT算法的一般流程归纳为:
- 初始化提升树模型:
f 0 ( x ) = a r g min c ∑ i = 1 N L ( y i , c ) f_0(x)=arg\min\limits_{c}\sum_{i=1}^{N}{L(y_i,c)} f0(x)=argcmini=1∑NL(yi,c)
-
对 m = 1 , . . . , M m=1,...,M m=1,...,M,有
- 对每个样本 i = 1 , . . . , N i=1,...,N i=1,...,N,计算负梯度拟合的残差
r m i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1 ( x ) r_{mi}=-[\frac{\partial{L(y_i,f(x_i))}}{\partial f(x_i)}]_{f(x)=f_{m-1}(x)} rmi=−[∂f(xi)∂L(yi,f(xi))]f(x)=fm−1(x)
- 将上一步得到的残差作为样本新的真实值,并将数据 ( x i , r m i ) , i = 1 , . . . , N (x_i,r_{mi}),i=1,...,N (xi,rmi),i=1,...,N作为下一棵树的训练数据,得到一棵新的回归树 f m ( x ) f_m(x) fm(x),其对应的叶子结点区域为 R m j , j = 1 , . . . , J R_{mj},j=1,...,J Rmj,j=1,...,J。其中 J J J为回归树 T T T的叶子结点个数。
- 对叶子区域 j = 1 , . . . , J j=1,...,J j=1,...,J计算最优拟合值:
c m j = a r g min c ∑ x i ∈ R m j L ( y i , f m − 1 ( x i ) + c ) c_{mj}=arg\min\limits_{c}\sum_{x_i\in R_{mj}}{L(y_i,f_{m-1}(x_i)+c)} cmj=argcminxi∈Rmj∑L(yi,fm−1(xi)+c)
- 更新提升树模型:
f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J c m j I ( x ∈ R m j ) f_m(x)=f_{m-1}(x)+\sum_{j=1}^{J}{c_{mj}I(x\in R_{mj})} fm(x)=fm−1(x)+j=1∑JcmjI(x∈Rmj)
-
得到最终的梯度提升树:
f ( x ) = f M ( x ) = ∑ m = 1 M ∑ j = 1 J c m j I ( x ∈ R m j ) f(x)=f_M(x)=\sum_{m=1}^{M}\sum_{j=1}^{J}{c_{mj}I(x\in R_{mj})} f(x)=fM(x)=m=1∑Mj=1∑JcmjI(x∈Rmj)
12.3 GBGT算法实现
编写GBGT算法,整体思路时从底层向上搭建。先编写决策树的树结点。基于决策树结点和决策树的一些特征,包括特征选择方法、生成方法和打印方法,来构建CART决策树,包括分类树和回归树。然后基于CART的基模型,结合前向分步算法和梯度提升,构建GBDT模型或者GBRT模型。
因此,从模型层面看GBDT的算法实现,是一个从树结点到CART基模型再到GBDT模型的过程
定义树结点、二叉决策树、CART分类树/回归树
import numpy as np
from utils import feature_split, calculate_gini
### 定义树结点
class TreeNode():
def __init__(self, feature_i=None, threshold=None,
leaf_value=None, left_branch=None, right_branch=None):
# 特征索引
self.feature_i = feature_i
# 特征划分阈值
self.threshold = threshold
# 叶子节点取值
self.leaf_value = leaf_value
# 左子树
self.left_branch = left_branch
# 右子树
self.right_branch = right_branch
### 定义二叉决策树
class BinaryDecisionTree(object):
### 决策树初始参数
def __init__(self, min_samples_split=2, min_gini_impurity=999,
max_depth=float("inf"), loss=None):
# 根结点
self.root = None
# 节点最小分裂样本数
self.min_samples_split = min_samples_split
# 节点初始化基尼不纯度
self.mini_gini_impurity = min_gini_impurity
# 树最大深度
self.max_depth = max_depth
# 基尼不纯度计算函数
self.gini_impurity_calculation = None
# 叶子节点值预测函数
self._leaf_value_calculation = None
# 损失函数
self.loss = loss
### 决策树拟合函数
def fit(self, X, y, loss=None):
# 递归构建决策树
self.root = self._build_tree(X, y)
self.loss=None
### 决策树构建函数
def _build_tree(self, X, y, current_depth=0):
# 初始化最小基尼不纯度
init_gini_impurity = 999
# 初始化最佳特征索引和阈值
best_criteria = None
# 初始化数据子集
best_sets = None
if len(np.shape(y)) == 1:
y = np.expand_dims(y, axis=1)
# 合并输入和标签
Xy = np.concatenate((X, y), axis=1)
# 获取样本数和特征数
n_samples, n_features = X.shape
# 设定决策树构建条件
# 训练样本数量大于节点最小分裂样本数且当前树深度小于最大深度
if n_samples >= self.min_samples_split and current_depth <= self.max_depth:
# 遍历计算每个特征的基尼不纯度
for feature_i in range(n_features):
# 获取第i特征的所有取值
feature_values = np.expand_dims(X[:, feature_i], axis=1)
# 获取第i个特征的唯一取值
unique_values = np.unique(feature_values)
# 遍历取值并寻找最佳特征分裂阈值
for threshold in unique_values:
# 特征节点二叉分裂
Xy1, Xy2 = feature_split(Xy, feature_i, threshold)
# 如果分裂后的子集大小都不为0
if len(Xy1) > 0 and len(Xy2) > 0:
# 获取两个子集的标签值
y1 = Xy1[:, n_features:]
y2 = Xy2[:, n_features:]
# 计算基尼不纯度
impurity = self.impurity_calculation(y, y1, y2)
# 获取最小基尼不纯度
# 最佳特征索引和分裂阈值
if impurity < init_gini_impurity:
init_gini_impurity = impurity
best_criteria = {"feature_i": feature_i, "threshold": threshold}
best_sets = {
"leftX": Xy1[:, :n_features],
"lefty": Xy1[:, n_features:],
"rightX": Xy2[:, :n_features],
"righty": Xy2[:, n_features:]
}
# 如果计算的最小不纯度小于设定的最小不纯度
if init_gini_impurity < self.mini_gini_impurity:
# 分别构建左右子树
left_branch = self._build_tree(best_sets["leftX"], best_sets["lefty"], current_depth + 1)
right_branch = self._build_tree(best_sets["rightX"], best_sets["righty"], current_depth + 1)
return TreeNode(feature_i=best_criteria["feature_i"], threshold=best_criteria["threshold"], left_branch=left_branch, right_branch=right_branch)
# 计算叶子计算取值
leaf_value = self._leaf_value_calculation(y)
return TreeNode(leaf_value=leaf_value)
### 定义二叉树值预测函数
def predict_value(self, x, tree=None):
if tree is None:
tree = self.root
# 如果叶子节点已有值,则直接返回已有值
if tree.leaf_value is not None:
return tree.leaf_value
# 选择特征并获取特征值
feature_value = x[tree.feature_i]
# 判断落入左子树还是右子树
branch = tree.right_branch
if isinstance(feature_value, int) or isinstance(feature_value, float):
if feature_value >= tree.threshold:
branch = tree.left_branch
elif feature_value == tree.threshold:
branch = tree.right_branch
# 测试子集
return self.predict_value(x, branch)
### 数据集预测函数
def predict(self, X):
y_pred = [self.predict_value(sample) for sample in X]
return y_pred
# CART分类树
class ClassificationTree(BinaryDecisionTree):
### 定义基尼不纯度计算过程
def _calculate_gini_impurity(self, y, y1, y2):
p = len(y1) / len(y)
gini = calculate_gini(y)
# 基尼不纯度
gini_impurity = p * calculate_gini(y1) + (1-p) * calculate_gini(y2)
return gini_impurity
### 多数投票
def _majority_vote(self, y):
most_common = None
max_count = 0
for label in np.unique(y):
# 统计多数
count = len(y[y == label])
if count > max_count:
most_common = label
max_count = count
return most_common
# 分类树拟合
def fit(self, X, y):
self.impurity_calculation = self._calculate_gini_impurity
self._leaf_value_calculation = self._majority_vote
super(ClassificationTree, self).fit(X, y)
### CART回归树
class RegressionTree(BinaryDecisionTree):
# 计算方差减少量
def _calculate_variance_reduction(self, y, y1, y2):
var_tot = np.var(y, axis=0)
var_y1 = np.var(y1, axis=0)
var_y2 = np.var(y2, axis=0)
frac_1 = len(y1) / len(y)
frac_2 = len(y2) / len(y)
# 计算方差减少量
variance_reduction = var_tot - (frac_1 * var_y1 + frac_2 * var_y2)
return sum(variance_reduction)
# 节点值取平均
def _mean_of_y(self, y):
value = np.mean(y, axis=0)
return value if len(value) > 1 else value[0]
# 回归树拟合
def fit(self, X, y):
self.impurity_calculation = self._calculate_variance_reduction
self._leaf_value_calculation = self._mean_of_y
super(RegressionTree, self).fit(X, y)
定义辅助函数
import numpy as np
### 定义二叉特征分裂函数
def feature_split(X, feature_i, threshold):
split_func = None
if isinstance(threshold, int) or isinstance(threshold, float):
split_func = lambda sample: sample[feature_i] >= threshold
else:
split_func = lambda sample: sample[feature_i] == threshold
X_left = np.array([sample for sample in X if split_func(sample)])
X_right = np.array([sample for sample in X if not split_func(sample)])
return np.array([X_left, X_right])
### 计算基尼指数
def calculate_gini(y):
y = y.tolist()
probs = [y.count(i)/len(y) for i in np.unique(y)]
gini = sum([p*(1-p) for p in probs])
return gini
### 打乱数据
def data_shuffle(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
12.3.1 基于Numpy的GBDT算法实现
导入模块
# 导入numpy
import numpy as np
# 导入CART模块(决策树结点、基础二叉决策树、CART分类树和CART回归树)
from cart import TreeNode, BinaryDecisionTree, ClassificationTree, RegressionTree
# 导入数据划分模块
from sklearn.model_selection import train_test_split
# 导入均方误差评估模块
from sklearn.metrics import mean_squared_error
# 导入辅助函数
from utils import feature_split, calculate_gini, data_shuffle
GBDT损失函数
### 定义回归树的平方损失
class SquareLoss():
# 定义平方损失
def loss(self, y, y_pred):
return 0.5 * np.power((y - y_pred), 2)
# 定义平方损失的梯度
def gradient(self, y, y_pred):
return -(y - y_pred)
GBDT类的定义
### GBDT定义
class GBDT(object):
def __init__(self, n_estimators, learning_rate, min_samples_split,
min_gini_impurity, max_depth, regression):
### 常用超参数
# 树的棵树
self.n_estimators = n_estimators
# 学习率
self.learning_rate = learning_rate
# 结点最小分裂样本数
self.min_samples_split = min_samples_split
# 结点最小基尼不纯度
self.min_gini_impurity = min_gini_impurity
# 最大深度
self.max_depth = max_depth
# 默认为回归树
self.regression = regression
# 损失为平方损失
self.loss = SquareLoss()
# 如果是分类树,需要定义分类树损失函数
# 这里省略,如需使用,需自定义分类损失函数
if not self.regression:
self.loss = None
# 多棵树叠加
self.estimators = []
for i in range(self.n_estimators):
self.estimators.append(RegressionTree(min_samples_split=self.min_samples_split,
min_gini_impurity=self.min_gini_impurity,
max_depth=self.max_depth))
# 拟合方法
def fit(self, X, y):
# 前向分步模型初始化,第一棵树
self.estimators[0].fit(X, y)
# 第一棵树的预测结果
y_pred = self.estimators[0].predict(X)
# 前向分步迭代训练
for i in range(1, self.n_estimators):
gradient = self.loss.gradient(y, y_pred)
self.estimators[i].fit(X, gradient)
y_pred -= np.multiply(self.learning_rate, self.estimators[i].predict(X))
# 预测方法
def predict(self, X):
# 回归树预测
y_pred = self.estimators[0].predict(X)
for i in range(1, self.n_estimators):
y_pred -= np.multiply(self.learning_rate, self.estimators[i].predict(X))
# 分类树预测
if not self.regression:
# 将预测值转化为概率
y_pred = np.exp(y_pred) / np.expand_dims(np.sum(np.exp(y_pred), axis=1), axis=1)
# 转化为预测标签
y_pred = np.argmax(y_pred, axis=1)
return y_pred
GBDT分类树和回归树
### GBDT分类树
class GBDTClassifier(GBDT):
def __init__(self, n_estimators=200, learning_rate=.5, min_samples_split=2,
min_info_gain=1e-6, max_depth=2):
super(GBDTClassifier, self).__init__(n_estimators=n_estimators,
learning_rate=learning_rate,
min_samples_split=min_samples_split,
min_gini_impurity=min_info_gain,
max_depth=max_depth,
regression=False)
# 拟合方法
def fit(self, X, y):
super(GBDTClassifier, self).fit(X, y)
### GBDT回归树
class GBDTRegressor(GBDT):
def __init__(self, n_estimators=300, learning_rate=0.1, min_samples_split=2,
min_var_reduction=1e-6, max_depth=3):
super(GBDTRegressor, self).__init__(n_estimators=n_estimators,
learning_rate=learning_rate,
min_samples_split=min_samples_split,
min_gini_impurity=min_var_reduction,
max_depth=max_depth,
regression=True)
GBDT算法测试
### GBDT分类树
# 导入数据集模块
from sklearn import datasets
# 导入波士顿房价数据集
boston = datasets.load_boston()
# 打乱数据集
X, y = shuffle_data(boston.data, boston.target, seed=13)
X = X.astype(np.float32)
offset = int(X.shape[0] * 0.9)
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 创建GBRT实例
model = GBDTRegressor()
# 模型训练
model.fit(X_train, y_train)
# 模型预测
y_pred = model.predict(X_test)
# 计算模型预测的均方误差
mse = mean_squared_error(y_test, y_pred)
print ("Mean Squared Error of NumPy GBRT:", mse)
12.3.2 基于sklearn的GBDT实现
# 导入GradientBoostingRegressor模块
from sklearn.ensemble import GradientBoostingRegressor
# 创建模型实例
reg = GradientBoostingRegressor(n_estimators=200, learning_rate=0.5,
max_depth=4, random_state=0)
# 模型拟合
reg.fit(X_train, y_train)
# 模型预测
y_pred = reg.predict(X_test)
# 计算模型预测的均方误差
mse = mean_squared_error(y_test, y_pred)
print ("Mean Squared Error of sklearn GBRT:", mse)
12.4 小结
- GBDT以CART为基模型的Boosting集成学习框架,梯度提升更有效的优化一般损失函数
- GBDT分梯度提升分类树和梯度提升回归树两种模型
第 13 章 XGBoost
参考:XGBoost: A Scalable Tree Boosting System
XGBoost是一种基于GBDT的顶级梯度提升模型,相比于GBDT,XGBoost最大特性在于对损失函数展开到二阶导数,使梯度提升树模型更逼近真实损失。
13.1 XGBoost 极度梯度提升树
XGBoost全称为 eXtreme Gradient Boosting ,译为极度梯度提升树,可参考论文 XGBoost: A Scalable Tree Boosting System
- 算法精度:XGBoost通过将损失函数展开到二阶导数,使得其能更逼近真实损失
- 算法速度:XGBoost使用加权分位数sketch和稀疏感知算法,通过缓存优化和模型并行来提高算法速度
- 泛化能力:XGBoots通过对损失函数加入正则化项、加性模型中设置缩减率和列抽样等方法防止模型过拟合
13.2 XGBoost原理推导
XGBoost是多个基模型线性组合成的加性模型,XGBoost表示为:
y ^ i = ∑ k = 1 K f k ( x i ) \hat{y}_i=\sum_{k=1}^{K}{f_k(x_i)} y^i=k=1∑Kfk(xi)
根据前向分步算法,假设第 t t t次迭代的基模型是 f t ( x ) f_t(x) ft(x),有:
y i ^ ( t ) = ∑ k = 1 t y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}^{(t)}=\sum_{k=1}^{t}{\hat{y_i}^{(t-1})}+f_t(x_i) yi^(t)=k=1∑tyi^(t−1)+ft(xi)
XGBoost损失函数基本形式由经验损失和正则化项构成:
L = ∑ i = 1 n l ( y i , y i ^ ) + ∑ i = 1 t Ω ( f i ) L=\sum_{i=1}^{n}{l(y_i,\hat{y_i})}+\sum_{i=1}^{t}{\Omega (f_i)} L=i=1∑nl(yi,yi^)+i=1∑tΩ(fi)
其中 ∑ i = 1 n l ( y i , y i ^ ) \sum_{i=1}^{n}{l(y_i,\hat{y_i})} ∑i=1nl(yi,yi^)为经验损失项,表示训练数据集预测值与真实值之间的损失; ∑ i = 1 t Ω ( f i ) \sum_{i=1}^{t}{\Omega (f_i)} ∑i=1tΩ(fi)为正则化项,表示全部 t t t棵树的复杂度之和。
根据前向分步的算法,以t步模型为例,假设模型对第 t t t个样本 x i x_i xi的预测值为:
y i ^ ( t ) = y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}^{(t)}=\hat{y_i}^{(t-1)}+f_t(x_i) yi^(t)=yi^(t−1)+ft(xi)
其中 y i ^ ( t − 1 ) \hat{y_i}^{(t-1)} yi^(t−1)是由第 t − 1 t-1 t−1步的模型给出的预测值,其作为一个已知常量存在, f t ( x i ) f_t(x_i) ft(xi)为第 t t t步树模型的预测值。因此损失函数改写为
同时对该式正则化项进行拆分,因为前 t − 1 t-1 t−1棵树的结构已经确定,所以前 t − 1 t-1 t−1棵树的复杂度之和可以表示为常数:
针对 l ( y i , y i ^ t − 1 + f t ( x i ) ) l(y_i,\hat{y_i}^{t-1}+f_t(x_i)) l(yi,yi^t−1+ft(xi))使用二阶泰勒公式,将相应的损失函数经验损失项写为:
其中 g i g_i gi为损失函数一阶导数, h i h_i hi为损失函数二阶导数,注意这里是对 y i ^ ( t − 1 ) \hat{y_i}^{(t-1)} yi^(t−1)求导。
将该二阶泰勒展开式带入改写后的损失函数中,可得损失函数的近似表达式:
去掉常数项,简化后的损失函数为:
因此,只需求解损失函数每一步的一阶导数和二阶导数值,并对目标函数进行优化求解,就可以得到前向分步中每一步的模型 f ( x ) f(x) f(x),最后根据加性模型得到XGBoost模型
假设一棵决策树是由叶子结点的权重 w w w和样本实例到叶子结点的映射关系 q q q构成【理解为决策树的分支结构】,所以一棵树的数学表达定义为:
f t ( x ) = w q ( x ) f_t(x)=w_q(x) ft(x)=wq(x)
定义决策树复杂度的正则化项。模型复杂度 Ω \Omega Ω可由单棵决策树的叶子结点树 T T T和叶子结点权重 w w w决定,即损失函数的复杂度由决策树的所有结点数和叶子权重决定。所以,模型复杂度表示为:
Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega(f_t)=\gamma T+\frac{1}{2}\lambda\sum_{j=1}^{T}{w_j^2} Ω(ft)=γT+21λj=1∑Twj2
下面对决策树所有叶子结点重新归组。将属于第 j j j个叶子结点的所有样本 x i x_i xi划入一个叶子结点的样本集合中,即 I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij={i∣q(xi)=j},因而XGBoost的损失函数继续改写为:
对于每个叶子结点 j j j,将其从损失函数中单独取出,
G j w j + 1 2 ( H j + λ ) w j 2 G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2 Gjwj+21(Hj+λ)wj2
由于该式是关于 w j w_j wj的二次函数,在树结构固定的情况下,进行求导,可得最优点和最优值:
假设决策树模型在某个结点进行特征分类,分类前损失函数是:
分裂后的损失函数为:
那么,分裂后的信息增益为:
如果增益 G a i n > 0 Gain>0 Gain>0,即分类为两个叶子结点后,损失函数下降了,则考虑此次分裂的结果。实际处理时需要遍历所有特征寻找最优分裂特征。
XGBoost推到思路和流程简化图:
13.3 XGBoost算法实现
13.3.1 XGBoost实现:基于GBDT的改进
辅助函数
import numpy as np
### 定义二叉特征分裂函数
def feature_split(X, feature_i, threshold):
split_func = None
if isinstance(threshold, int) or isinstance(threshold, float):
split_func = lambda sample: sample[feature_i] >= threshold
else:
split_func = lambda sample: sample[feature_i] == threshold
X_left = np.array([sample for sample in X if split_func(sample)])
X_right = np.array([sample for sample in X if not split_func(sample)])
return np.array([X_left, X_right])
### 计算基尼指数
def calculate_gini(y):
y = y.tolist()
probs = [y.count(i)/len(y) for i in np.unique(y)]
gini = sum([p*(1-p) for p in probs])
return gini
### 打乱数据
def data_shuffle(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
### 类别标签转换
def cat_label_convert(y, n_col=None):
if not n_col:
n_col = np.amax(y) + 1
one_hot = np.zeros((y.shape[0], n_col))
one_hot[np.arange(y.shape[0]), y] = 1
return one_hot
XGBoost单棵回归树类
import numpy as np
from cart import TreeNode, BinaryDecisionTree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from utils import cat_label_convert
### XGBoost单棵树类
class XGBoost_Single_Tree(BinaryDecisionTree):
# 结点分裂方法
def node_split(self, y):
# 中间特征所在列
feature = int(np.shape(y)[1]/2)
# 左子树为真实值,右子树为预测值
y_true, y_pred = y[:, :feature], y[:, feature:]
return y_true, y_pred
# 信息增益计算方法
def gain(self, y, y_pred):
# 梯度计算
Gradient = np.power((y * self.loss.gradient(y, y_pred)).sum(), 2)
# Hessian矩阵计算
Hessian = self.loss.hess(y, y_pred).sum()
return 0.5 * (Gradient / Hessian)
# 树分裂增益计算
# 式(12.28)
def gain_xgb(self, y, y1, y2):
# 结点分裂
y_true, y_pred = self.node_split(y)
y1, y1_pred = self.node_split(y1)
y2, y2_pred = self.node_split(y2)
true_gain = self.gain(y1, y1_pred)
false_gain = self.gain(y2, y2_pred)
gain = self.gain(y_true, y_pred)
return true_gain + false_gain - gain
# 计算叶子结点最优权重
def leaf_weight(self, y):
y_true, y_pred = self.node_split(y)
# 梯度计算
gradient = np.sum(y_true * self.loss.gradient(y_true, y_pred), axis=0)
# hessian矩阵计算
hessian = np.sum(self.loss.hess(y_true, y_pred), axis=0)
# 叶子结点得分
leaf_weight = gradient / hessian
return leaf_weight
# 树拟合方法
def fit(self, X, y):
self.impurity_calculation = self.gain_xgb
self._leaf_value_calculation = self.leaf_weight
super(XGBoost_Single_Tree, self).fit(X, y)
XGBoost分类损失函数
### 分类损失函数定义
# 定义Sigmoid类
class Sigmoid:
def __call__(self, x):
return 1 / (1 + np.exp(-x))
def gradient(self, x):
return self.__call__(x) * (1 - self.__call__(x))
# 定义Logit损失
class LogisticLoss:
def __init__(self):
sigmoid = Sigmoid()
self._func = sigmoid
self._grad = sigmoid.gradient
# 定义损失函数形式
def loss(self, y, y_pred):
y_pred = np.clip(y_pred, 1e-15, 1 - 1e-15)
p = self._func(y_pred)
return y * np.log(p) + (1 - y) * np.log(1 - p)
# 定义一阶梯度
def gradient(self, y, y_pred):
p = self._func(y_pred)
return -(y - p)
# 定义二阶梯度
def hess(self, y, y_pred):
p = self._func(y_pred)
return p * (1 - p)
XGBoost模型
### XGBoost定义
class XGBoost:
def __init__(self, n_estimators=300, learning_rate=0.001,
min_samples_split=2,
min_gini_impurity=999,
max_depth=2):
# 树的棵树
self.n_estimators = n_estimators
# 学习率
self.learning_rate = learning_rate
# 结点分裂最小样本数
self.min_samples_split = min_samples_split
# 结点最小基尼不纯度
self.min_gini_impurity = min_gini_impurity
# 树最大深度
self.max_depth = max_depth
# 用于分类的对数损失
# 回归任务可定义平方损失
# self.loss = SquaresLoss()
self.loss = LogisticLoss()
# 初始化分类树列表
self.trees = []
# 遍历构造每一棵决策树
for _ in range(n_estimators):
tree = XGBoost_Single_Tree(
min_samples_split=self.min_samples_split,
min_gini_impurity=self.min_gini_impurity,
max_depth=self.max_depth,
loss=self.loss)
self.trees.append(tree)
# xgboost拟合方法
def fit(self, X, y):
y = cat_label_convert(y)
y_pred = np.zeros(np.shape(y))
# 拟合每一棵树后进行结果累加
for i in range(self.n_estimators):
tree = self.trees[i]
y_true_pred = np.concatenate((y, y_pred), axis=1)
tree.fit(X, y_true_pred)
iter_pred = tree.predict(X)
y_pred -= np.multiply(self.learning_rate, iter_pred)
# xgboost预测方法
def predict(self, X):
y_pred = None
# 遍历预测
for tree in self.trees:
iter_pred = tree.predict(X)
if y_pred is None:
y_pred = np.zeros_like(iter_pred)
y_pred -= np.multiply(self.learning_rate, iter_pred)
y_pred = np.exp(y_pred) / np.sum(np.exp(y_pred), axis=1, keepdims=True)
# 将概率预测转换为标签
y_pred = np.argmax(y_pred, axis=1)
return y_pred
XGBoost代码测试
from sklearn import datasets
# 导入鸢尾花数据集
data = datasets.load_iris()
# 获取输入输出
X, y = data.data, data.target
# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=43)
# 创建xgboost分类器
clf = XGBoost()
# 模型拟合
clf.fit(X_train, y_train)
# 模型预测
y_pred = clf.predict(X_test)
# 准确率评估
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy: ", accuracy)
13.3.2 基于原生库示例
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
# 设置模型参数
params = {
'booster': 'gbtree',
'objective': 'multi:softmax',
'num_class': 3,
'gamma': 0.1,
'max_depth': 2,
'lambda': 2,
'subsample': 0.7,
'colsample_bytree': 0.7,
'min_child_weight': 3,
'eta': 0.001,
'seed': 1000,
'nthread': 4,
}
dtrain = xgb.DMatrix(X_train, y_train)
num_rounds = 200
model = xgb.train(params, dtrain, num_rounds)
# 对测试集进行预测
dtest = xgb.DMatrix(X_test)
y_pred = model.predict(dtest)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print ("Accuracy:", accuracy)
# 绘制特征重要性
plot_importance(model)
plt.show();
13.4 小结
- XGBoost将损失函数展开到二阶导数,使得梯度提升树模型更逼近真实损失
- 从最初的损失函数版本,进行二阶泰勒展开并重新定义一棵决策树,通过对叶子结点分组得到最终损失函数形式,最后求最优点和最优取值,并得到叶子结点的分裂标准
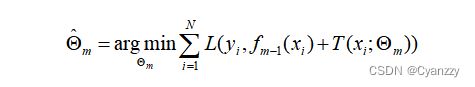
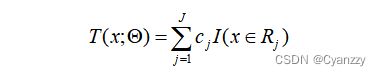
![[机器学习入门笔记] 3.监督学习集成模型部分_第1张图片](http://img.e-com-net.com/image/info8/93991cac0d414bb5b1eb0732b8df3bbb.png)

![[机器学习入门笔记] 3.监督学习集成模型部分_第2张图片](http://img.e-com-net.com/image/info8/a1d3968481e141e9b2930714a5d11f57.png)
![[机器学习入门笔记] 3.监督学习集成模型部分_第3张图片](http://img.e-com-net.com/image/info8/b89974d4e3bc4dbf8ccfc43c71b2902f.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第4张图片](http://img.e-com-net.com/image/info8/aa4c94b0a96341a3b9aac7fda9f72e10.jpg)
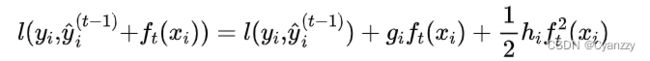
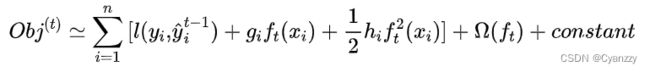
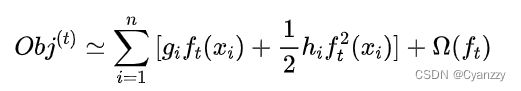
![[机器学习入门笔记] 3.监督学习集成模型部分_第5张图片](http://img.e-com-net.com/image/info8/647ee41d68ba4339b96565b090ad25fa.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第6张图片](http://img.e-com-net.com/image/info8/8ed4ea9b013e4c9cb4c16ac2c4166a6b.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第7张图片](http://img.e-com-net.com/image/info8/54e686dbb99948329c1782c7b9e63ab0.jpg)
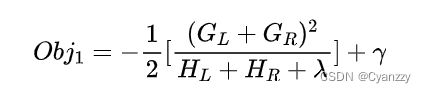

![[机器学习入门笔记] 3.监督学习集成模型部分_第8张图片](http://img.e-com-net.com/image/info8/f9a408462793428f96479e1feb2f9d65.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第9张图片](http://img.e-com-net.com/image/info8/9e243b3ef1fc4e42873fa7c1e33d816b.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第10张图片](http://img.e-com-net.com/image/info8/c772e6ad0ceb4ba29e76a66aa6e1a8c4.jpg)
![[机器学习入门笔记] 3.监督学习集成模型部分_第11张图片](http://img.e-com-net.com/image/info8/c41d4122267c405086ce8841800096cc.jpg)