论文阅读《ACVNet: Attention Concatenation Volume for Accurate and Efficient Stereo Matching》

论文地址：https://arxiv.org/pdf/2203.02146.pdf
源码地址：https://github.com/gangweiX/ACVNet

---

概述

出发点：

• GwcNet直接拼接特征构建代价体的方式带来冗余特征
• 匹配代价体可以隐式地反映一幅图像中相邻像素之间的关系，即相邻属于同一类的像素往往具有相近的相似性。

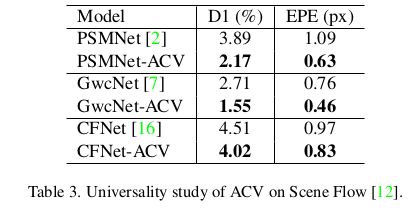
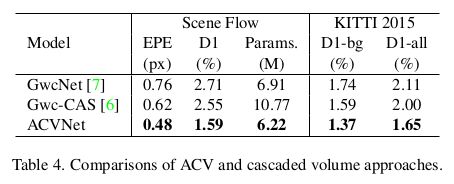
  Cost Volume在立体匹配中至关重要，本文提出一种基于注意力权重的代价体构建方法，此方法可以去除冗余信息，保留与匹配相关的信息；此外，提出一种多层级自适应的块匹配策略来得到具有区分性的匹配特征，该方法可以提高弱（无）纹理区域的特征表达能力；所构建的代价体Attention Concatenation Vloume (ACV) 可以作为子模块接入到其它模型中，使得模型轻量化的同时提升精度。

---

模型架构

Attention concatenation volume

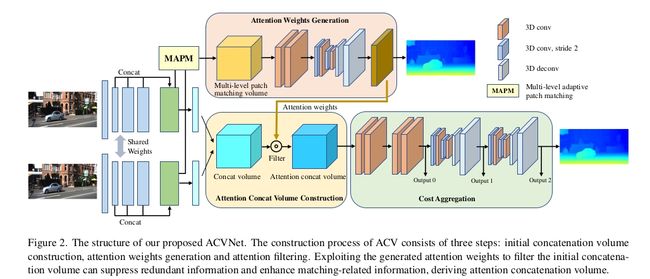
  注意力组合代价体主要包含三个部分：初始拼接代价体构建、注意力权重生成模块、注意力滤波模块；

初始代价体构建

  给定输入图像对 $I_l、I_R\in R^{H\times W\times 3}$，先经过权值共享的特征提取模块得到特征向量，将左右视图的特征向量降维到32维：$f_l、f_r\in R^{N_c\times \frac{H}{4}\times \frac{W}{4}}(N_c=32)$ ，初始的代价体由左右视图的特征体直接拼接而来，如式1所示：
$${\mathbf{C}}_{\text{concat }}(\cdot ,d,x,y)=\text{ Concat }\left\{{\mathbf{f}}_l(x,y),{\mathbf{f}}_r(x-d,y)\right\}\text{\hspace{1em}(1)}$$
其中 $c_{concat}\in R^{2N_c\times \frac{D}{4}\times \frac{H}{4}\times \frac{W}{4}}$，D代表视差的最大值；

注意力权重生成

  注意力权重的作用是抑制初始代价体中任务无关的信息，增强任务相关的信息。为此，将左右视图的相关性中提取的几何信息生成注意权值。弱纹理区域无法提供有效的匹配信息，使用传统的方法来构建点对点的匹配代价是不可靠的；为了解决这个问题，本文提出了基于多尺度自适应块匹配鲁棒的匹配代价构建方法（multi-level adaptive patch match：MAPM）；

用公式表示此过程：

记第g组的特征表示为 $f_l^g,f_r^g$，则$C_{patch}$ 可以表示为：
$$\begin{array}{c}{\mathbf{C}}_{patch}^{l_k}(g,d,x,y)=\frac{1}{N_f/N_g}{\sum }_{(i,j)\in {\Omega }^k}{\omega }_{ij}^k\cdot C_{ij}^g(d,x,y)\\ \\ C_{ij}^g(d,x,y)=⟨{\mathbf{f}}_l^g(x-i,y-j),{\mathbf{f}}_r^g(x-i-d,y-j)⟩\end{array}\text{\hspace{1em}(2)}$$
其中 $C_{patch}^{l_k}$表示第k level的匹配代价，$<.，.>$ 表示内积，$(x,y)$ 表示像素位置，$d$ 表示视差值， ${\Omega }^k=(i,j),(i,j\in (-k,0,k))$表示邻域像素（如图3所示，表示不同空洞卷积采集到的像素），$w_{ij}^k$ 表示可学习的权重（空洞卷积卷积核的参数）；

  首先通过左右视图的注意力权重构建特征图 ($N_f=320$) ，沿着channel维度分组$N_g=40$，再使用分组内积的方式得到Group-Wise Correlation Vloume $\in R^{b\times N_g\times \frac{d_{max}}{4}\times \frac{h}{4}\times \frac{w}{4}}$（这个代价体用于求注意力权重, ），0-8组作为$l_1$特征图，8-24组作为 $l_2$ ，24-40 组作为$l_3$，对于每个$l_1、l_2、l_3$ 特征，使用不同扩张率的空洞卷积核处理得到不同尺度的特征图$C_{patch}^{l_1}、C_{patch}^{l_2}、C_{patch}^{l_3}$

  将三个patch的特征图拼接：
$${\mathbf{C}}_{\text{patch }}=\text{ Concat }\left\{{\mathbf{C}}_{\text{patch }}^{l_1},{\mathbf{C}}_{\text{patch }}^{l_2},{\mathbf{C}}_{\text{patch }}^{l_3}\right\}\in R^{b\times N_g\times \frac{d_{max}}{4}\times \frac{h}{4}\times \frac{w}{4}}\text{\hspace{1em}(3)}$$

  使用3D卷积与3D U-Net对其正则化，最后使用3D卷积将其channel维度压缩为1，得到注意力权重$A\in R^{b\times 1\times \frac{d_{max}}{4}\times \frac{h}{4}\times \frac{w}{4}}$

使用视差GT来监督注意力权重A的学习，使用arg softmax来对A回归得到视差图，并与GT求smmoth L1损失；

Attention filtering

  使用注意力权重来去除初始代价体中冗余的信息，如式4所示：
$${\mathbf{C}}_{ACV}(i)=\mathbf{A}\odot {\mathbf{C}}_{\text{concat }}(i)\text{\hspace{1em}(4)}$$

其中 $\odot$ 表示点乘。

ACVNet 架构

  ACVNet主要包含以下部分：特征提取、注意力权重体构建、代价聚合、视差预测；

特征提取

  使用2D CNN提取左右视图的特征图，得到原图大小为1/4的特征图，使用stride为1的CNN分别得到 channel为64， 128， 128大小为原图尺寸 1/4 的特征图，然后将其沿channel维度拼接得到注意力构建特征图 $\in R^{b\times 320\times \frac{H}{4}\times \frac{W}{4}}$，最后使用CNN将其维度压缩到32 的匹配代价体构建特征图 $\in R^{b\times 32\times \frac{H}{4}\times \frac{W}{4}}$；

注意力权重体构建

  使用320通道的注意力权重构建特征图得到注意力权重体，使用32通道的匹配代价体构建特征图构建初始匹配代价体；然后使用注意力权重对初始匹配代价体进行滤波；

代价体正则化

  使用4个3D卷积和2个堆叠的3D U-Net网络进行代价体正则化,得到out1、out2、out3，如图2所示

视差计算

  基于期望的形式计算视差图：
$$d=\sum _{k=0}^{D_{\max }-1}k\cdot p_k\text{\hspace{1em}(5)}$$

ACVNet-Fast 架构

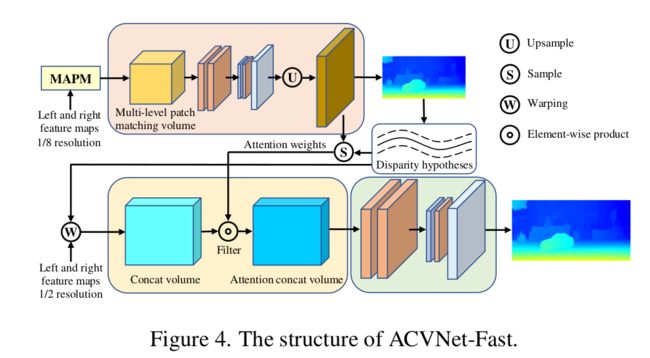
  Fast版本主要区别是使用注意力全重体生成视差图，然后使用该视差图来上下采样得到深度范围比较窄的视差假设体与注意力全重体，最后使用其来求视差图；

---

损失函数

ACVNet的损失函数如式6所示：
$$\begin{array}{r}L={\lambda }_{att}\cdot {\mathrm{Smooth}}_{L_1}\left({\mathbf{d}}_{att}-{\mathbf{d}}^{gt}\right)+{\sum }_{i=0}^{i=2}{\lambda }_i\cdot {\mathrm{Smooth}}_{L_1}\left({\mathbf{d}}_i-{\mathbf{d}}^{gt}\right)\end{array}\text{\hspace{1em}(6)}$$
其中 $d_{att}$ 为注意力体回归得到的视差图，$d_i$ 表示$ou{t}_i$ 回归得到的视差图；

ACVNet-Fast的损失函数如式7所示：
$$L^f={\lambda }_{att}^f\cdot {\mathrm{Smooth}}_{L_1}\left({\mathbf{d}}_{att}^f-{\mathbf{d}}^{gt}\right)+{\lambda }^f\cdot {\text{ Smooth }}_{L_1}\left({\mathbf{d}}^f-{\mathbf{d}}^{gt}\right)\text{\hspace{1em}(7)}$$

---

实验结果