四足机器人(三)--- 姿态控制
四足机器人(三)--- 姿态控制
- 概述
- 姿态表示
- 使用MATLAB实现姿态控制算法
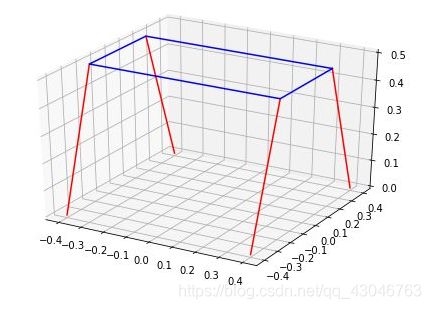
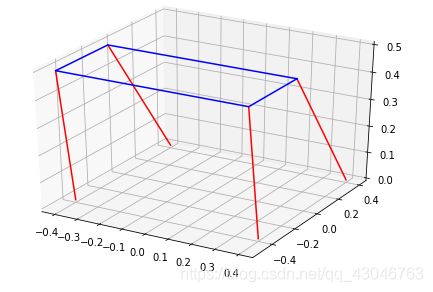
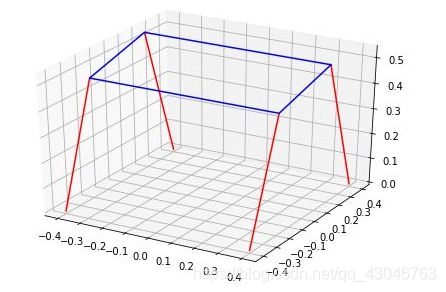
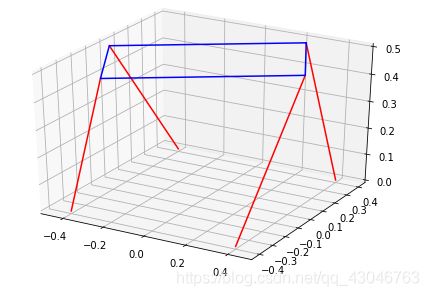
- 效果
概述
四足机器人运动过程中,身体部分的姿态会不断地发生变化。假如机器人的足端一直保持与地面接触且相对位置不发生变化,此时的身体姿态我们称之为站立姿态。
四足机器人的站立姿态控制,本质上是并联机器人的逆解。只不过相比于并联机器人每条支腿只有一个驱动自由度、平台自由度和驱动自由度一般相等而言,四足机器人存在许多冗余自由度。因此在解算出每条腿的位置向量后,还需要对每条腿做逆解(而不是像并联机器人那样直接得到线位移)。在这里我们默认单腿的逆解已知。
姿态表示
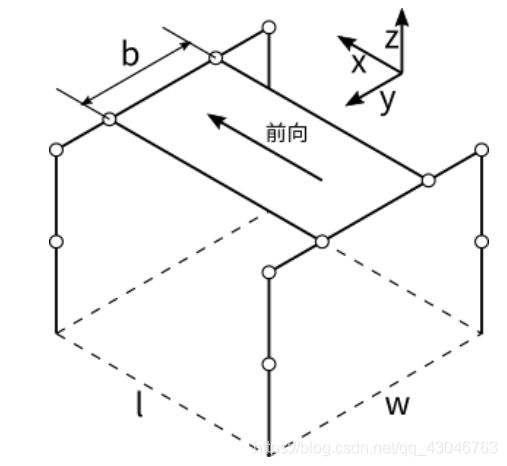
其中,l 和 w分别表示机器人足端在长度与宽度,b表示两前足基座原点之间的距离。

移除后腿后 ,其中, O 为地面坐标系原点,位于足端位置的对角线交点; O’ 为身体部分几何中心。
我们使用齐次变换矩阵 A 来表示机器人身体部分的位姿:
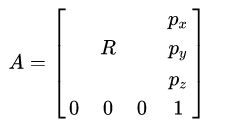
其中 pn 为向量OO’ 的坐标分量,表示位置:![]()
R 为身体相对于地面的旋转矩阵,表示姿态(RPY为欧拉角):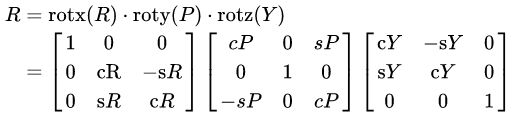
使用MATLAB实现姿态控制算法
rpy_r = 0;
rpy_p = 40;
rpy_y = 0;
pos_x = 0;
pos_y = 0;
pos_z = 190;
b = 160;
w = 210;
l = 440;
R = rpy_r*pi/180;
P = rpy_p*pi/180;
Y = rpy_y*pi/180;
pos = [pos_x,pos_y,pos_z]';
rotx = ([[1, 0, 0 ]
[0, cos(R), -sin(R)]
[0, sin(R), cos(R)]]);
roty = ([[cos(P), 0, -sin(P)]
[0, 1, 0 ]
[sin(P), 0, cos(P)]]);
rotz = ([[cos(Y), -sin(Y), 0]
[sin(Y), cos(Y), 0]
[ 0, 0, 1]]);
rot_mat = rotx * roty * rotz;
%结构参数
body_struc = ([[l/2, b/2, 0]
[l/2, -b/2, 0]
[-l/2, b/2, 0]
[-l/2, -b/2, 0]])';
footpoint_struc = ([[l/2, w/2-70, 0]
[l/2, -w/2-20, 0]
[-l/2, w/2-70, 0]
[-l/2, -w/2-20, 0]])';
leg_pose = zeros(3,4);
for i = 1:4
leg_pose(:,i) = pos + rot_mat * body_struc(:,i) - footpoint_struc(:,i);
end
rf_x = (leg_pose(1,1));
rf_y = (leg_pose(2,1));
rf_z = (leg_pose(3,1));
lf_x = (leg_pose(1,2));
lf_y = (leg_pose(2,2));
lf_z = (leg_pose(3,2));
rb_x = (leg_pose(1,3));
rb_y = (leg_pose(2,3));
rb_z = (leg_pose(3,3));
lb_x = (leg_pose(1,4));
lb_y = (leg_pose(2,4));
lb_z = (leg_pose(3,4));