基于粒子群优化深度置信网络的分类预测

1.深度置信网络(DBN)

DBN 由一层 BP 神经网络和若干层 RBM 栈式叠加而成。最顶层的 softmax 回归层作为标签层输出分类识别的结果， 其余层完成特征提取。DBN 的学习训练过程可以划分为预训练和微调两个阶段。第一阶段为预训练阶段，把网络中任 意相邻两层当作是一个 RBM，即以下层 RBM 模型 的输出作为上层 RBM 模型的输入，利用贪心无监 督学习算法逐层对整个 DBN 模型参数进行初始化。 用贪心无监督学习方法逐层训练之后，深层架构底 层的原始特征被组合成更加紧凑的高层次特征。 由于贪心算法无法使整个网络参数达到最优，故需 要进入微调阶段优化整个网络的参数。第二阶段为 微调阶段，整个深层架构传统的全局学习算法(BP 或 wake-sleep 算法)有监督地对网络空间的相关 参数进行进一步优化和调整，自顶向下微调整个模 型。这种先无监督学习后监督学习的两步走模式， 使 DBN 在训练数据不足的半监督学习任务中有很 好的表现。同时，这种训练模式通过无监督训练 有效地缩小参数寻优的空间，大大减少了有监督训练的时间。

2. 粒子群优化算法

隐藏层的层数和每层的单元数对分类精度的影响很大。一般根据认为经验设置，本代码采用粒子群优化算法优化DBN的网络隐含层节点数。

3.部分代码

%%pso-dbn
num_class = 3;                          % 分类类别个数
dbn.sizes = [10, 5, 5];                 % DBN各层神经元个数
opts.numepochs = 300;                   % RBM 训练时 迭代次数
opts.batchsize = 30;                    % 每次使用10个样本进行训练
opts.momentum  =  0;                    % 学习率的动量
opts.alpha     =  0.01;                 % 学习率因子
opts.fig = 0;                           % 关闭画图


%% 建立DBN模型
dbn = dbnsetup(dbn, p_train, opts);  


%% 参数初始化
c1      =   50;     % 学习因子
c2      =    5;     % 学习因子
maxgen  =   20;     % 种群更新次数  
sizepop =    3;     % 种群规模
Vmax    =   10;     % 最大速度
Vmin    =  - 4;     % 最小速度
popmax  =  100;     % 最大边界
popmin  =    5;     % 最小边界


%% 节点总数
numsum = length(dbn.sizes) - 1;


for i = 1 : sizepop
    pop(i, :) = (rands(1, numsum) + 1) * 10;
    V(i, :) = (rands(1, numsum) + 1) * 10;
    fitness(i) = fun(pop(i, :), numsum, dbn, p_train, t_train, opts, num_class);
end


%% 个体极值和群体极值
[fitnesszbest, bestindex] = min(fitness);
zbest = pop(bestindex, :);     % 全局最佳
gbest = pop;                   % 个体最佳
fitnessgbest = fitness;        % 个体最佳适应度值
BestFit = fitnesszbest;        % 全局最佳适应度值


%% 迭代寻优
for i = 1 : maxgen
    for j = 1 : sizepop
        %速度更新
        V(j, :) = V(j, :) + c1 * rand * (gbest(j, :) - pop(j, :)) + c2 * rand * (zbest - pop(j, :));
        V(j,(V(j, :) > Vmax)) = Vmax;
        V(j,(V(j, :) < Vmin)) = Vmin;
        
        %种群更新
        pop(j, :) = pop(j, :) + 0.2 * V(j, :);
        pop(j, (pop(j, :) > popmax)) = popmax;
        pop(j, (pop(j, :) < popmin)) = popmin;
        
        %自适应变异
        pos = unidrnd(numsum);
        if rand > 0.95
            pop(j, pos) = rands(1, 1);
        end
        
        %适应度值
        fitness(j) = fun(pop, numsum, dbn, p_train, t_train, opts, num_class);
    end
    
    for j = 1 : sizepop
        
        %个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j, :) = pop(j, :);
            fitnessgbest(j) = fitness(j);
        end


        %群体最优更新 
        if fitness(j) < fitnesszbest
            zbest = pop(j, :);
            fitnesszbest = fitness(j);
        end 
    end
    BestFit = [BestFit, fitnesszbest];    
end


%% 提取
for i = 1 : numsum
    dbn.sizes(i + 1) = round(pop(i));
end


%%  训练DBN模型
dbn.sizes(1) = [];
dbn = dbnsetup(dbn, p_train, opts);  
dbn = dbntrain(dbn, p_train, opts);   


%% DBN移植到深层NN
nn = dbnunfoldtonn(dbn, num_class);   % 反向微调
nn.activation_function = 'sigm';      % 激活函数


%% 反向调整DBN
opts.numepochs = 1500;                    % 反向微调次数
opts.alpha     = 0.001;                   % 学习率因子
opts.batchsize = 30;                      % 反向微调每次样本数
opts.output = 'softmax';                  % 激活函数
opts.fig = 1;                             % 打开画图
nn = nntrain(nn, p_train, t_train, opts); % 训练


%% 预测 
T_sim1 = nnpredict(nn, p_train); 
T_sim2 = nnpredict(nn, p_test);


%% 性能评价
error1 = sum(T_sim1' == T_train) / M * 100;
error2 = sum(T_test' == T_sim2) / N * 100;


%%  绘图
figure
plot(1:M,T_train,'r*',1:M,T_sim1,'bo','LineWidth',1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string={'训练集预测结果对比';['准确率=' num2str(error1) '%']};
title(string)
grid


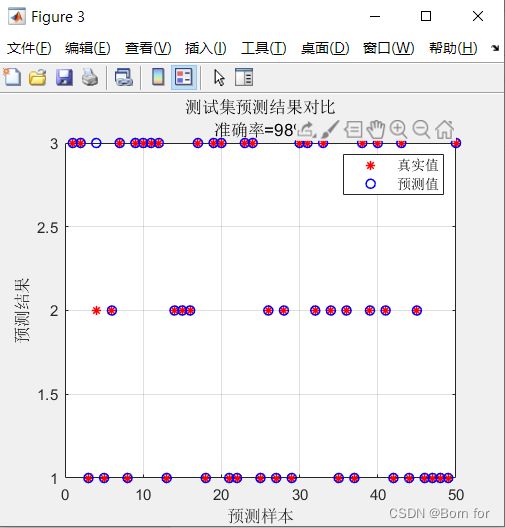
figure
plot(1 : N, T_test, 'r*', 1:N,T_sim2,'bo','LineWidth',1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string={'测试集预测结果对比';['准确率=' num2str(error2) '%']};
title(string)
grid


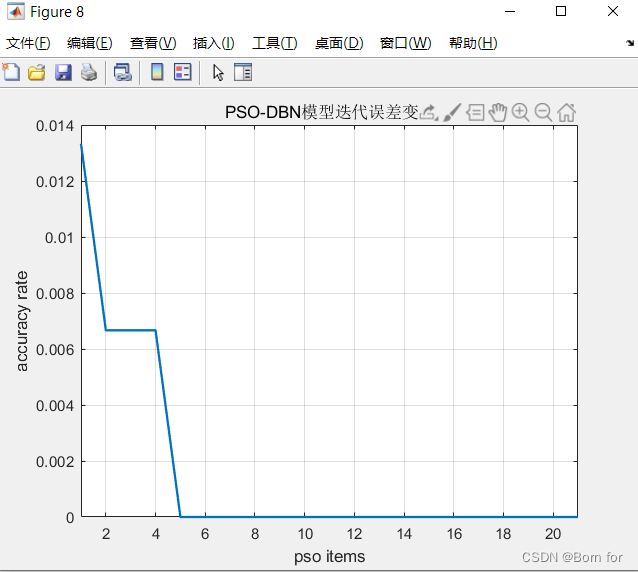
%% PSO 优化迭代图
figure;
P0 = plot(1 : length(BestFit), BestFit, 'LineWidth', 1.5);
xlabel('pso items');
ylabel('accuracy rate');
xlim([1, length(BestFit)])
string = {'PSO-DBN模型迭代误差变化'};
title(string)
grid on

4.结果展示

 

 完整代码见基于粒子群优化深度置信网络的分类预测-数据 (mianbaoduo.com)