初始GRU - 门控循环单元(RNN循环神经网络)

重置门与更新门

我们首先介绍重置门（reset gate）和更新门（update gate）。 我们把它们设计成$(0,1)$区间中的向量， 这样我们就可以进行凸组合。

1、重置门允许我们控制“可能还想记住”的过去状态的数量；

2、更新门将允许我们控制新状态中有多少个是旧状态的副本。

两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

其图示如下:

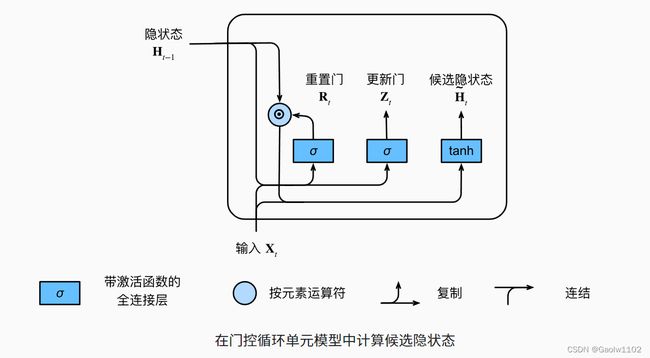
重置门

核心公式如下:

$$H^{con}=tanh(X_h{W}_{xh}+(R_t\odot H_{t-1})W_{hh}+b_h)$$

其中，$H^{con}$ 为 候选隐状态， $R_t$ 为 重置门。

当重置门 $R_t\to 1$ 时，即此时候选隐状态恢复一个普通的循环神经网络；
当重置门 $R_t\to 0$ 时，即此时候选隐状态恢复一个普通的多层感知机模型。

其图示如下:

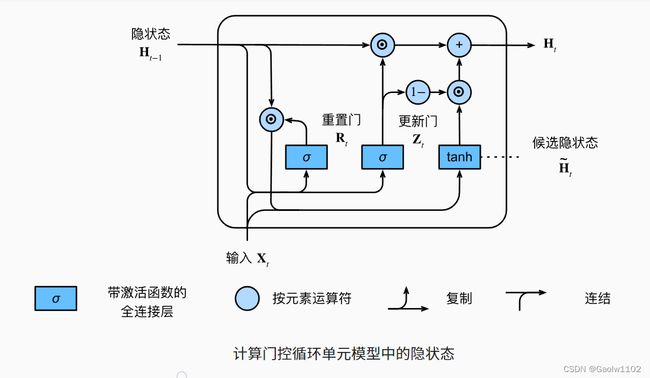
更新门

核心公式如下:

$$H=Z_t\odot H_{t-1}+(1-Z_t)\odot H^{con}$$

其中，$H$ 为 更新后的隐状态， $Z_t$ 为 更新门。

当重置门 $Z_t\to 1$ 时，即此时更新后的隐状态跳过时间序列的影响，造成 $H_t=H_{t-1}$，来自 $X_t$ 的信息基本被忽略 ;当重置门 $Z_t\to 0$ 时，即此时更新后的隐状态即近似为候选隐状态。

其图示如下:

---

总之，门控循环单元具有以下两个显著特征:

• 重置门有助于捕获序列中的短期依赖关系。

• 更新门有助于捕获序列中的长期依赖关系。

从零开始实现

为了更好地理解门控循环单元模型，我们从零开始实现它。

import torch
from torch import nn
from d2l import torch as d2l

batch_size, num_steps = 32, 35                                                    #定义数据批量大小为32
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)             #加载训练集迭代器、词典

初始化模型参数

下一步是初始化模型参数。我们从标准差为0.01的高斯分布中提取权重，并将偏置项设为0，超参数num_hiddens定义隐藏单元的数量，实例化与更新门、重置门、候选隐状态和输出层相关的所有权重和偏置。

def get_params(vocab_size, num_hiddens, device):
    
    num_inputs = num_outputs = vocab_size
    
    def normal(shape):
        return torch.randn(size=shape, device=device)*0.01
    
    def three():
        return (normal((num_inputs, num_hiddens)),
                normal((num_hiddens, num_hiddens)),
               torch.zeros(num_hiddens, device=device))
    
    W_xz, W_hz, b_z = three()             #更新门的参数
    W_xr, W_hr, b_r = three()             #重置门的参数
    W_xh, W_hh, b_h = three()             #候选隐状态参数
    
    #输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    
    #附加梯度信息
    params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    
    #返回参数信息
    return params

定义模型

现在我们将定义隐状态的初始化函数 init_gru_state 。与之前定义的 init_rnn_state 函数一样，此函数返回一个形状为（批量大小，隐藏单元个数）的张量，张量的值全部为零。

def init_gru_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

现在我们准备定义门控循环单元模型，模型的架构与基本的循环神经网络单元是相同的，只是权重更新公式更为复杂。

def gru(inputs, state, params):
    #返回所有的参数信息
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    
    H, = state
    outputs = []
    
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)                   #计算更新门的值
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)                   #计算重置门的值
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)          #计算候选隐状态condicate_state
        H = Z * H + (1 - Z) * H_tilda                                      #计算新的隐状态
        Y = H @ W_hq + b_q                                                 #计算输出Y
        outputs.append(Y)                                                  #追加结果
    
    #返回输出结果Y与新的隐藏状态H
    return torch.cat(outputs, dim=0), (H, )

训练与预测

训练和预测的工作与之前完全相同。训练结束后，我们分别打印输出训练集的困惑度，以及前缀 “time traveler” 和 “travler” 的预测序列上的困惑度。

#定义词典的大小vocab_size，隐状态个数num_hiddens
vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu()

num_epochs, lr = 500, 1                      #迭代次数为500次

#定义GRU门控循环单元模型
model = d2l.RNNModelScratch(vocab_size, num_hiddens, device, get_params, init_gru_state, gru)

#训练模型
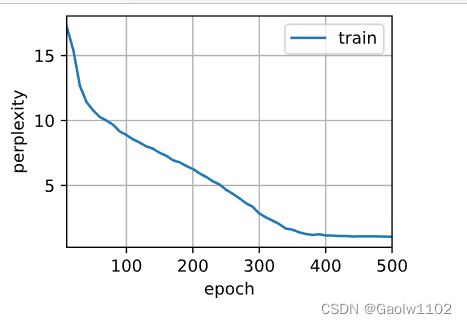
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

perplexity 1.0, 11850.6 tokens/sec on cpu
time travelleryou can show black is white by argument said filby
traveller with a slight accession ofcheerfulness really thi

简洁实现

高级API包含了前文介绍的所有配置细节， 所以我们可以直接实例化门控循环单元模型。 这段代码的运行速度要快得多， 因为它使用的是编译好的运算符而不是Python来处理之前阐述的许多细节。

num_inputs = vocab_size                                          #输出模型特征数
gru_layer = nn.GRU(num_inputs, num_hiddens)                      #定义gru层
model = d2l.RNNModel(gru_layer, len(vocab))                      #定义GRU模型
model = model.to(device)

# 训练模型
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

perplexity 1.1, 11819.6 tokens/sec on cpu
time travelleryou can show black is white by argument said filby
travelleryou can show black is white by argument said filby

小结

1.门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系。

2.重置门有助于捕获序列中的短期依赖关系。

3.更新门有助于捕获序列中的长期依赖关系。

4.重置门打开时，门控循环单元包含基本循环神经网络；更新门打开时，门控循环单元可以跳过子序列。