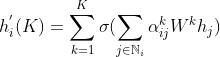图神经网络及其Pytorch实现
图结构一般而言是十分不规则的，可以认为是无限维的一种数据，因此不存在平移不变性。每一个结点周围的结构都是独一无二的，因此针对该结构的数据。涌现出GNN、DeepWalk、node2vec等等方法。
GCN，即图卷积神经网络
图卷积神经网络（GCN）
tkipf/pygcn (github.com)
Graph Convolutional Networks | Thomas Kipf | University of Amsterdam (tkipf.github.io)
图卷积网络（GCN）
数学基础：拉普拉斯算子、傅里叶变换
GCN，即图卷积神经网络，实际上跟CNN的作用一样，是一个特征提取器，只不过操作对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而可以使用特征对图数据进行节点分类(node classification)，图分类(graph classification)，边预测(link prediction)，图嵌入表示(graph embedding)。
GCN是一个神经网络层，层与层之间的传播方式为：
， 
是单位矩阵
是
的度矩阵（degree matrix）， 公式
是每一层的特征，对于输入层而言，
是非线性激活函数
使用GCN公式可以很好地提取图的特征。GCN输入的一个图，通过若干层GCN每个node的特征从X变成Z。但是，无论中间有多少层，node之间的连接关系，即A，是共享的。
倘若构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播公式为：
每一层GCN的输入都是邻接矩阵A和node的特征矩阵H，直接做一个内积，再乘以一个参数矩阵W，再使用一个激活函数
由于没有加单位矩阵，因此计算node的所有邻居特征加权和，但是忽略node本身的特征- 是未经过归一化的矩阵，因此与特征矩阵相乘会改变特征原本的分布，因此需要对进行标准化处理， 归一化矩阵：
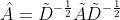
谱图卷积的核心就是使用对称归一化拉普拉斯矩阵，也是GCN卷积叫法的来历。GCN原文中给出完整的从普图卷积到GCN的推导。
class GraphConvolution(nn.Module):
'''
Simple GCN layer
'''
def __init__(self, in_features, out_features, dropout, bias = True):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.dropout = nn.Dropout(dropout)
self.weight = nn.Parameter(torch.Tensor(in_features, out_features))
nn.init.xavier_uniform_(self.weight) #xavier初始化，
if bias:
self.bias = nn.Parameter(torch.Tensor(out_features))
nn.init.zeros_(self.bias)
else:
self.register_parameter('bias', None)
def forward(self, input, adj):
# inputs: (N, n_channels), adj: sparse_matrix (N, N)
support = torch.mm(self.dropout(inputs), self.weight)
output = torch.spmm(adj, support)
if self.bias is not None:
return output + self.bias
else:
return output
class GCN(nn.Module):
def __init__(self, n_features, hidden_dim, dropout, n_classes):
super(GCN, self).__init__()
self.first_layer = GraphConvolution(n_features, hidden_dim, dropout)
self.last_layer = GraphConvolution(hidden_dim, n_classes, dropout)
self.dropout = nn.Dropout(dropout)
self.relu = nn.ReLU()
def forward(self, inputs, adj):
x = self.relu(self.first_layer(inputs, adj))
x = self.dropout(x)
x = self.last_layer(x, adj)
return F.log_softmax(x, dim = 1)图注意力网络（GAT）
参考链接：
GAT（图注意力模型）
通过Pytorch深入理解GAT
pyGAT的Github仓库
A Gentle Introduction to Graph Neural Networks (distill.pub) [ 深度好文 ]
一、GAT基础知识
1.Graph数据结构的两种“特征”
对于graph或者network的数据结构，通常包含着顶点和边的关系。研究目标聚焦在顶点之上，边诉说着顶点之间的关系。
（1）对于任意一个顶点
, 它在图上邻居
， 构成第一种特征，即图的结构关系。
（2）除了图的结构之外，每个顶点还有自己的特征
（通常是一个高维向量）。
graph上的deep learning方法无非就是希望学习上面的两种特征。
2.GCN的局限性
GCN是处理transductive任务的一把利器。然而GCN存在两大局限性：
- 处理inductive任务的困难。
- 处理有向图的瓶颈， 不容易实现分配不同的学习权重给不同的neighbor。
3.Mask graph attention VS. Global graph attention
GAT本质上存在两种运算方式
（1）Global graph attention
顾名思义，就是每一个顶点都对于图上任意顶点都进行attention运算。
优点：完全不依赖于图的结构，对于inductive任务无压力
缺点：丢掉了图结构的这个特征，效果可能很差；运算面临着高昂的成本
（2）Mask graph attention
注意力机制的运算只在邻居顶点上进行。GAT作者在文中采用的是masked attention。
二、GAT模型
同所有的attention mechanism一样， GAT计算分为：（1）计算注意力系数（2）加权求和
1.计算注意力系数（attention coefficient）
对于顶点，逐个计算其邻居节点
和它自己之间的相似系数
![e_{ij} = a([Wh_{i} || Wh_{j}]), j \in \mathbb{N}_{i}](http://img.e-com-net.com/image/info8/ccfcf0818f2b4671b13b6d2b1e59fc85.gif){kind=small}
公式解读：首先一个共享参数
的线性映射对于顶点的特征进行增加特征维度（一种常见的特征增强(feature augment)方法）； ![[ \cdot || \cdot ]](http://img.e-com-net.com/image/info8/1b2e7917ce8e4d7fbc2240f8c47541e6.gif){kind=small}
对于顶点
的变换后的特征进行拼接（concatenate）；
将拼接的高维特征映射为一个实数。作者是通过single-layer feedforward neural network实现的。
学习顶点之间的相关性，就是通过可学习的参数和映射完成的。有了相关系数，使用softmax进行归一化即可转换成为注意力系数。
2.加权求和（aggregate）
根据计算好的注意力系数，把特征加权求和(aggregate)一下。
就是GAT输出的对于每个顶点的新特征（融合了邻域信息），
是激活函数
attention需要multi-head提高性能，增强后的融合公式如下：
三、代码实现
使用pytorch进行代码实现
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import networkx as nx
def get_weights(size, gain=1.414):
weights = nn.Parameter(torch.zeros(size=size))
nn.init.xavier_uniform_(weights, gain=gain)
return weights
class GraphAttentionLayer(nn.Module):
'''
Simple GAT layer 图注意力层 (inductive graph)
'''
def __init__(self, in_features, out_features, dropout, alpha, concat = True, head_id = 0):
''' One head GAT '''
super(GraphAttentionLayer, self).__init__()
self.in_features = in_features #节点表示向量的输入特征维度
self.out_features = out_features #节点表示向量的输出特征维度
self.dropout = dropout #dropout参数
self.alpha = alpha #leakyrelu激活的参数
self.concat = concat #如果为true，再进行elu激活
self.head_id = head_id #表示多头注意力的编号
self.W_type = nn.ParameterList()
self.a_type = nn.ParameterList()
self.n_type = 1 #表示边的种类
for i in range(self.n_type):
self.W_type.append(get_weights((in_features, out_features)))
self.a_type.append(get_weights((out_features * 2, 1)))
#定义可训练参数，即论文中的W和a
self.W = nn.Parameter(torch.zeros(size = (in_features, out_features)))
nn.init.xavier_uniform_(self.W.data, gain = 1.414) #xavier初始化
self.a = nn.Parameter(torch.zeros(size = (2 * out_features, 1)))
nn.init.xavier_uniform_(self.a.data, gain = 1.414) #xavier初始化
#定义dropout函数防止过拟合
self.dropout_attn = nn.Dropout(self.dropout)
#定义leakyrelu激活函数
self.leakyrelu = nn.LeakyReLU(self.alpha)
def forward(self, node_input, adj, node_mask = None):
'''
node_input: [batch_size, node_num, feature_size] feature_size 表示节点的输入特征向量维度
adj: [batch_size, node_num, node_num] 图的邻接矩阵
node_mask: [batch_size, node_mask]
'''
zero_vec = torch.zeros_like(adj)
scores = torch.zeros_like(adj)
for i in range(self.n_type):
h = torch.matmul(node_input, self.W_type[i])
h = self.dropout_attn(h)
N, E, d = h.shape # N == batch_size, E == node_num, d == feature_size
a_input = torch.cat([h.repeat(1, 1, E).view(N, E * E, -1), h.repeat(1, E, 1)], dim = -1)
a_input = a_input.view(-1, E, E, 2 * d) #([batch_size, E, E, out_features])
score = self.leakyrelu(torch.matmul(a_input, self.a_type[i]).squeeze(-1)) #([batch_size, E, E, 1]) => ([batch_size, E, E])
#图注意力相关系数（未归一化）
zero_vec = zero_vec.to(score.dtype)
scores = scores.to(score.dtype)
scores += torch.where(adj == i+1, score, zero_vec.to(score.dtype))
zero_vec = -1*30 * torch.ones_like(scores) #将没有连接的边置为负无穷
attention = torch.where(adj > 0, scores, zero_vec.to(scores.dtype)) #([batch_size, E, E])
# 表示如果邻接矩阵元素大于0时，则两个节点有连接，则该位置的注意力系数保留；否则需要mask并置为非常小的值，softmax的时候最小值不会被考虑
if node_mask is not None:
node_mask = node_mask.unsqueeze(-1)
h = h * node_mask #对结点进行mask
attention = F.softmax(attention, dim = 2) #[batch_size, E, E], softmax之后形状保持不变，得到归一化的注意力权重
h = attention.unsqueeze(3) * h.unsqueeze(2) #[batch_size, E, E, d]
h_prime = torch.sum(h, dim = 1) #[batch_size, E, d]
# h_prime = torch.matmul(attention, h) #[batch_size, E, E] * [batch_size, E, d] => [batch_size, N, d]
#得到由周围节点通过注意力权重进行更新的表示
if self.concat:
return F.elu(h_prime)
else:
return h_prime
class GAT(nn.Module):
def __init__(self, in_dim, hid_dim, dropout, alpha, n_heads, concat = True):
'''
Dense version of GAT
in_dim输入表示的特征维度、hid_dim输出表示的特征维度
n_heads 表示有几个GAL层，最后进行拼接在一起，类似于self-attention从不同的子空间进行抽取特征
'''
super(GAT, self).__init__()
assert hid_dim % n_heads == 0
self.dropout = dropout
self.alpha = alpha
self.concat = concat
self.attn_funcs = nn.ModuleList()
for i in range(n_heads):
self.attn_funcs.append(
#定义multi-head的图注意力层
GraphAttentionLayer(in_features = in_dim, out_features = hid_dim // n_heads,
dropout = dropout, alpha = alpha, concat = concat, head_id = i)
)
self.dropout = nn.Dropout(self.dropout)
def forward(self, node_input, adj, node_mask = None):
'''
node_input: [batch_size, node_num, feature_size] 输入图中结点的特征
adj: [batch_size, node_num, node_num] 图邻接矩阵
node_mask: [batch_size, node_num] 表示输入节点是否被mask
'''
hidden_list = []
for attn in self.attn_funcs:
h = attn(node_input, adj, node_mask = node_mask)
hidden_list.append(h)
h = torch.cat(hidden_list, dim = -1)
h = self.dropout(h) #dropout函数防止过拟合
x = F.elu(h) #激活函数
return x
#特征矩阵
x = torch.randn((2, 4, 8))
#邻接矩阵
adj = torch.tensor([[[0, 1, 0, 1],
[1, 0, 1, 0],
[0, 1, 0, 1],
[1, 0, 1, 0]]])
adj = adj.repeat(2, 1, 1)
#mask矩阵
node_mask = torch.Tensor([[1, 0, 0, 1],
[0, 1, 1, 1]])
gat_layer = GraphAttentionLayer(in_features = 8, out_features = 8, dropout = 0.1, alpha = 0.2, concat = True) #输入特征维度8， 输出特征维度8， 使用多头注意力机制
gat_ = GAT(in_dim = 8, hid_dim = 8, dropout = 0.1, alpha = 0.2, n_heads = 2, concat = True) #输入特征维度8， 输出特征维度8, 使用多头注意力机制
output_ = gat_(x, adj, node_mask)
print(output_.shape)
output_ = gat_(x, adj, node_mask)
print(output_.shape)
#输出：
torch.Size([2, 4, 8])
torch.Size([2, 4, 8])