《Python数据分析与挖掘实战》第9章——svm

本文是基于《Python数据分析与挖掘实战》的实战部分的第9章的数据——《基于水色图像的水质评价》做的分析。

旨在补充原文中的细节代码，并给出文中涉及到的内容的完整代码。

在作者所给代码的基础上增加的内容包括： 

1）数据预处理部分：切割图片、使用颜色矩方法进行特征提取 

2）画混淆矩阵图

备注：水质图像的下载链接：http://pan.baidu.com/s/1geRwH4v 密码：7n72

1 背景与目标分析

    利用图像处理技术，通过水色图像实现水质的自动评价

    实质：多分类问题

2  数据预处理

图片数据特征提取:常用直方图法、颜色矩；此代码用的是颜色矩方法（具体原因，原书中也已经有详细的讲解）

2.1分别求出不同类别的图像数据对应的颜色矩表格

f __name__ == '__main__':
    # 待切割的图片所在的目录（多个图片所在的目录，是个列表格式）【分别求出不同类别的数据对应的特征值】
    doc = r'D:\PycharmProjects\sf_dataAnalysis\waterimg\images\1'

    # 获取图片路径：根据需求是否需要包含子文件夹中的图片文件（若需要，使用方式1，否则，使用方式2）
    # waitcut = getimgdir(doc) #注意：方式1、获取的当前工作目录下的所有图片文件(包含所有子文件夹的图片）
    waitcut = getimgdir_designed(doc)#注意：方式2、获取指定目录下的图片文件(不包含子文件夹的图片，仅当前文件夹）

    # 输入图片输出路径（若不存在，则新建目录）
    dstpath = saveimg(raw_input('请输入图片输出目录：')) # 例如，输入：D:\PycharmProjects\readwriteFiles\img_cut_pix\pic_cut
    resultlist = [[]] # 创建空列表用于存储切割后的文件的路径名
    while True:
        try:
            halfh = input('请输入切割后图片高的一半(数值）：') # 设定输入为50
            halfw = input('请输入切割后图片宽的一半（数值）：') # 设定输入为50
            print '正在批处理切割图片...'
            for i in waitcut:#所有图片文件路径
                filename = splitimage(i, halfh, halfw, dstpath)
                impix = color_moments(filename)
                resultlist.append(impix)
            print '图片切割完成！'
        except Exception:# 此处异常包括 (1) 输入的是非数值型（2）输入的数值是非正数 ！注意：如果数值过大，不影响切割，会超出原图
            print Exception
        else:
            break
    del resultlist[0]
    columnsname= ['R通道一阶矩','G通道一阶矩','B通道一阶矩','R通道二阶矩','G通道二阶矩','B通道二阶矩',\
                  'R通道三阶矩','G通道三阶矩','B通道三阶矩',]
    df =  DataFrame(resultlist,columns=columnsname)
    df.insert(0, 'typenum', 1)
    df.to_csv('type1.csv',encoding='gbk',index=False)

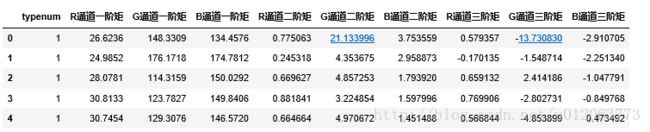
    print df

对于类别1的图像的颜色矩的值如下：

该过程中用到的函数定义如下：

# 获取当前工作目录及子目录下所有图片文件的绝对路径，包含其所有子文件夹中的图片
def getimgdir(imgfilename):
    imgdirs = []
    imgTypes = [".png", ".jpg", ".bmp"]
    if imgfilename:
        presentfiles = imgfilename
    else:
        presentfiles = os.getcwd()  # 获得当前工作目录

    for root, dirs, files in os.walk("."):
        r = root[2:]
        for afile in files:
            if r != '':
                ffile = presentfiles + "\\" + r + "\\" + afile
            else:
                ffile = presentfiles + "\\" + afile

            if ffile[ffile.rindex("."):].lower() in imgTypes:
                imgdirs.append(ffile)
    return imgdirs

# 获取当前工作目录及子目录下所有图片文件的绝对路径 # 不包含下层文件夹中的图片
def getimgdir_designed(imgfilename):
    if os.path.exists(imgfilename)== False:# 若指定的文件夹不存在，则提示！
        print '你设定的指定文件夹不存在！'
        return None
    imgdirs = []
    imgTypes = [".png", ".jpg", ".bmp"]
    presentfiles = imgfilename#获得当前工作目录
    recursion = 0  # 控制递归深度，只递归当前目录
    for root, dirs, files in os.walk(presentfiles):
        for afile in files:
            ffile = presentfiles + "\\" + afile
            if ffile[ffile.rindex("."):].lower() in imgTypes:
                imgdirs.append(ffile)
        if (not recursion):
            break
    return imgdirs

'''将图片切割成（2*halfw）*（2*halfh）像素的文件，并返回切割后的文件的绝对路径
src是待切割的文件的绝对路径，halfw是切割后图片的宽度的一半, 
halfh是切割后图片的长度的一半，dstpath是切割后图片的保存路径
注意：在切割图片时，要先确保要处理的图片中央位置是有效图片，若不是，则需要进行图片处理'''
def splitimage(src, halfw, halfh, dstpath):
    img = Image.open(src)
    w, h = img.size

    s = os.path.split(src)
    if dstpath == '':
        dstpath = s[0]
    fn = s[1].split('.')
    basename = fn[0]
    ext = fn[-1]

    box = (h // 2 - halfh, w // 2 - halfw, h // 2 + halfh, w // 2 + halfw)
    pic_cut_name = os.path.join(dstpath, basename + '_cut' + '.' + ext)
    img.crop(box).save(pic_cut_name)
    return pic_cut_name

# 颜色矩方式进行特征提取
def color_moments(filename):
    img = cv2.imread(filename)
    if img is None:
        return
    # Convert BGR to HSV colorspace
    hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
    # Split the channels - h,s,v
    h, s, v = cv2.split(hsv)
    # 初始化颜色特征
    color_feature = []

    # 一阶中心矩求解 sum(x)/N = mean  ---均值
    h_mean = np.mean(h)  # np.sum(h)/float(N)
    s_mean = np.mean(s)  # np.sum(s)/float(N)
    v_mean = np.mean(v)  # np.sum(v)/float(N)
    color_feature.extend([h_mean, s_mean, v_mean])
    # 二阶中心矩求解 (sum(x-mean)/N)**(1/2) = std ---方差
    h_std = np.std(h)  # np.sqrt(np.mean(abs(h - h.mean())**2))
    s_std = np.std(s)  # np.sqrt(np.mean(abs(s - s.mean())**2))
    v_std = np.std(v)  # np.sqrt(np.mean(abs(v - v.mean())**2))
    color_feature.extend([h_std, s_std, v_std])
    # 三阶中心矩求解 ((sum(x-mean))**(1/3)/N)**(1/3)
    h_skewness = np.mean((h - h.mean())**3)
    s_skewness = np.mean((s - s.mean())**3)
    v_skewness = np.mean((v - v.mean())**3)
    h_thirdMoment = abs(h_skewness)**(1./3) * (-1 if h_skewness < 0 else 1)
    s_thirdMoment = abs(s_skewness)**(1./3) * (-1 if s_skewness < 0 else 1)
    v_thirdMoment = abs(v_skewness)**(1./3) * (-1 if v_skewness < 0 else 1)
    color_feature.extend([h_thirdMoment, s_thirdMoment, v_thirdMoment])

    return color_feature

# 输出图片输出目录
def saveimg(dstpath):
    # if not dstpath or dstpath .isspace()
    if (os.path.exists(dstpath) == False) and  dstpath != '': # 若输入的路径不存在，则创建该目录
        os.makedirs(dstpath)  # 创建目标文件夹
    if dstpath == '': #不输入路径(直接回车）则表示使用源图片所在目录
        dstpath = os.getcwd()
    return dstpath

2.2 各个不同类别的水质的颜色矩都求出之后，连接各个数据

import pandas as pd
from pandas import DataFrame
import numpy as np


# 读取类型1的表格中的颜色矩数据
d1 = pd.read_csv('type1.csv',encoding="gbk")
# 读取类型2的表格中的颜色矩数据
d2 = pd.read_csv('type2.csv',encoding="gbk")
# 读取类型3的表格中的颜色矩数据
d3 = pd.read_csv('type3.csv',encoding="gbk")
# 读取类型4的表格中的颜色矩数据
d4 = pd.read_csv('type4.csv',encoding="gbk")
# 读取类型5的表格中的颜色矩数据
d5 = pd.read_csv('type5.csv',encoding="gbk")

ALLDATA = pd.concat([d1,d2,d3,d4,d5],ignore_index=True) # 做表格连接
ALLDATA.to_excel('ALLDATA.xlsx',index=False) # 存储数据

说明：求颜色矩之前需要将各个图片进行切割，但是，观察切割后的图片可以发现，有些图片的初始状态不在原图中央，使得切割后的图片还有较多白边，因此，笔者建议，若要想提高分类的准确度，后续可以尝试先手动将原始图片进行大致的切割，使得接下来要统一切割的时候，切到的图片都是能反映事实水质的图片。

3 模型构建

inputfile = 'moment.csv'
data = pd.read_csv(inputfile, encoding='gbk')
# 注意，此处不能用shuffle
sampler = np.random.permutation(len(data))
d = data.take(sampler).as_matrix()

data_train = d[:int(0.8*len(data)),:] #选取前80%做训练集
data_test = d[int(0.8*len(data)):,:] #选取后20%做测试集

# 构建支持向量机模型代码
x_train = data_train[:, 2:]*30 #由于特征的取值均在0-1之间，直接使用会使得区分度较小，因此此处进行 放大特征
y_train = data_train[:,0].astype(int)
x_test = data_test[:, 2:]*30 #放大特征
y_test = data_test[:,0].astype(int)

# 导入模型相关的支持向量机函数  建立并且训练模型
from sklearn import svm 
model = svm.SVC()
model.fit(x_train, y_train)
import pickle
pickle.dump(model, open('svcmodel.model','wb'))# model = pickle.load(open('svcmodel.model','rb'))


cm_train = metrics.confusion_matrix(y_train, model.predict(x_train)) # 训练样本的混淆矩阵
cm_test = metrics.confusion_matrix(y_test, model.predict(x_test)) # 测试样本的混淆矩阵

df1 = DataFrame(cm_train, index = range(1,6), columns=range(1,6))
df2 = DataFrame(cm_test, index = range(1,6), columns=range(1,6))
df1.to_excel('trainPre.xlsx')
df2.to_excel('testPre.xlsx')
print model.score(x_train,y_train) # 评价模型训练的准确率
print model.score(x_test,y_test) # 评价模型测试的准确率

备注：本章节完整代码详见 点击打开链接