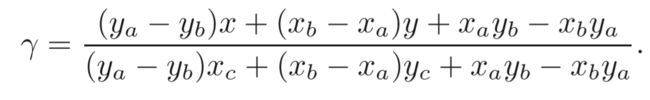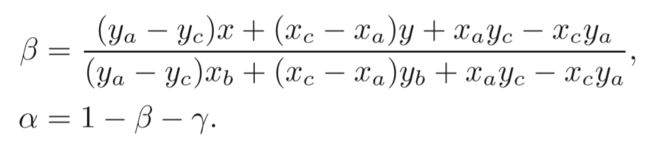计算机图形学三(补充)：重心坐标(barycentric coordinates)详解及其作用

(本篇文章同步发表于知乎专栏：https://zhuanlan.zhihu.com/p/144360079 欢迎三连关注)

本节会详细介绍重心坐标的定义以及解法,并简略的提及重心坐标在图形学中的运用(具体的运用会在之后的笔记中给出)

1 重心坐标的定义及求解

1.1 基础定义

给定三角形的三点坐标A, B, C，该平面内一点(x,y)可以写成这三点坐标的线性组合形式，即 $(x,y)=\alpha A+\beta B+\gamma C$ 且满足 $\alpha +\beta +\gamma =1$ 则称此时3个坐标A,B,C的权重$\alpha ,\beta ,\gamma$为点$(x,y)$的重心坐标。

（特别的，如图中所说的，如果该点在三角形内部则三点坐标都为非负数，我们会在1.3节给出简要的叙述。）

1.2 几何面积角度求解

除却1.1节中重心坐标的基础定义之外，重心坐标还有一个另外一个角度的等价定义，如下图：

将一点(x,y)与A,B,C三点直接连接，构成三个三角形面积分别为$A_A,A_B,A_C$,即可直接定义出重心坐标如图中公式所示。

(tips：如果这个点在某个边的外侧，那么该点与这条边构成的三角形面积计算为负值(不想深究的读者可暂时忽略这条tips))

好了根据这条定义，我们只需求出各个三角形的面积便可以直接得出重心坐标了！

我们已知图中4点坐标，那么求出面积自然是很简单的，这里利用行列式的几何意义直接求解，即任意2个2维向量组合成矩阵的行列式的绝对值，为这两条向量所围成平行四边形的面积 (如果对行列式几何意义不清楚的话建议前往B站搜索3B1B的线代本质)。设任意一点为P(x,y)，则由：

$A_B=|AP,AC|$, 其中AP,AC为列向量 符号||为行列式
$A_C=|AB,AP|$
$A_A=|BC,BP|$

此处省略行列式计算步骤，不难得出

注意，求出其中2个之后第三个可以根据性质直接求出。

1.3 坐标系角度求解

针对重心坐标系的另外一种等价视角便是，以A点为原点，AB,AC分别为新的坐标系的单位向量构建坐标系，如图所示：

其中给定任意点P的坐标可以用 $\beta ,\gamma$来表示，即$P(\beta ,\gamma )$,不难得出，P点坐标在原坐标系中的位置满足：

进一步化简得到：

到这里其实就可以发现，我们已经成功的把P用三角形的三个顶点的线性组合表示了，并且3个权重之和为1，完全符合定义，因此这是一种完全等价的角度！

从这种角度出发，我们完全可以将上式表现成一个线性方程组来求解出$\beta ,\gamma$，两个未知量，两个式子，如下：

解出该方程组的解其实与1.2节中面积的角度式完全一样的，不在这里展开。

最后我们看一下在1.1节所说的3个重心坐标都是非负的时候，点一定在三角形内，你是否可以从本节的坐标系角度之中直接看出呢？

2 重心坐标的运用

重心坐标在图形学中最重要的运用便是插值，他可以根据三个顶点A,B,C的属性插值出任意点的属性，无论是位置，颜色，深度，法线向量等等，而这些属性在之后的着色或是消除隐藏曲面都有很大的作用。这里只举一个在计算机图形学三：光栅化1(直线的数值微分算法,中点Brensenham算法, 三角形的光栅化中所提到的光栅化三角行的具体运用，即判断一个点是否在三角形内，完全可以用本节的重心坐标是否都大于0来代替之前的叉乘(其实二者一定程度上是等价的)。利用该条件来进行sample 再判断是否画出该像素。

这里还有一个小问题上一节中没有提到就是，如果一个点正好处于两个三角形的公共边之上那么，这个点该算作是哪个三角的呢

答案是只要你自己规定好就行，无所谓算哪个三角形的！

在虎书（Fundamentals of Computer Graphics 4th）中作者利用了取任意屏幕外一点判断该公共边所对应的点是否与该点处于公共边同一侧来判断这个点的归属。具体可以参考虎书的8.1节

最后如果本文对你有帮助求点赞求收藏求一个大大的关注 ，后序会持续更新，感谢阅读！

Reference

[1] Fundamentals of Computer Graphics 4th
[2] GAMES101-现代计算机图形学入门-闫令琪