探索增强型灰狼优化算法
文章目录
- 一、理论基础
-
- 1、灰狼优化算法
- 2、探索增强型灰狼优化算法
-
- (1)改进的位置更新公式
- (2)非线性控制参数策略
- (3)EEGWO算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、灰狼优化算法
请参考这里。
2、探索增强型灰狼优化算法
(1)改进的位置更新公式
为了增强GWO的性能,研究其位置更新公式是目前比较活跃的研究方向。受PSO的启发,为了加强探索性能,利用另一个个体的信息来指导候选个体的搜索,将GWO所描述的位置更新公式改进为: X → ( t + 1 ) = b 1 × r 3 × X → 1 ( t ) + X → 2 ( t ) + X → 3 ( t ) 3 + b 2 × r 4 × ( X → ′ − X → ) (1) \overrightarrow X(t+1)=b_1\times r_3\times\frac{\overrightarrow X_1(t)+\overrightarrow X_2(t)+\overrightarrow X_3(t)}{3}+b_2\times r_4\times\left(\overrightarrow X'-\overrightarrow X\right)\tag{1} X(t+1)=b1×r3×3X1(t)+X2(t)+X3(t)+b2×r4×(X′−X)(1)其中, X → ′ \overrightarrow X' X′是从种群中随机选择的不同于 X → \overrightarrow X X的一个个体, r 3 r_3 r3和 r 4 r_4 r4均为 [ 0 , 1 ] [0,1] [0,1]之间的随机数, b 1 ∈ ( 0 , 1 ] b_1\in(0,1] b1∈(0,1]和 b 2 ∈ ( 0 , 1 ] b_2\in(0,1] b2∈(0,1]是用于调整探索和开发能力的常数。
(2)非线性控制参数策略
在原始的GWO算法中,控制参数 a → \overrightarrow a a的值从2线性减小到0。由于GWO算法的搜索过程是非线性和高度复杂的,线性控制参数 a → \overrightarrow a a策略不能真正反映实际的搜索过程。此外,如果控制参数 a → \overrightarrow a a被选择为非线性递减量,而不是线性递减策略,将获得更好的性能。基于上述考虑,与之前的其他工作不同,修改了控制参数 a → \overrightarrow a a,如下所示: a → ( t ) = a i n i t i a l − ( a i n i t i a l − a f i n a l ) × ( M a x _ i t e r − t M a x _ i t e r ) μ (2) \overrightarrow a(t)=a_{initial}-(a_{initial}-a_{final})\times\left(\frac{Max\_iter-t}{Max\_iter}\right)^\mu\tag{2} a(t)=ainitial−(ainitial−afinal)×(Max_iterMax_iter−t)μ(2)其中, t t t表示当前迭代次数, M a x _ i t e r Max\_iter Max_iter表示最大迭代次数, μ \mu μ表示非线性调整指数, a i n i t i a l a_{initial} ainitial和 a f i n a l a_{final} afinal分别表示控制参数 a → \overrightarrow a a的初始值和终止值。
图1展示了控制参数 a → \overrightarrow a a随不同的 μ \mu μ值的变化曲线。

(3)EEGWO算法伪代码
基于上述(1)(2)两种策略的探索增强型灰狼优化算法(Exploration-enhanced grey wolf optimizer algorithm, EEGWO)的伪代码如图2所示。

二、仿真实验与结果分析
将EEGWO与GWO进行对比,以文献[1]中表1的F3、F4、F5(单峰函数/30维)、F15、F16、F17(多峰函数/30维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:
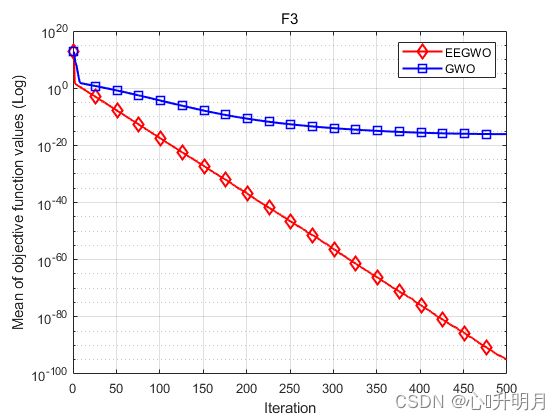




函数:F3
EEGWO:最差值: 2.5769e-94, 最优值: 1.0205e-98, 平均值: 1.4073e-95, 标准差: 4.7701e-95, 秩和检验: 1
GWO:最差值: 1.7092e-16, 最优值: 2.2252e-17, 平均值: 8.4678e-17, 标准差: 3.9515e-17, 秩和检验: 3.0199e-11
函数:F4
EEGWO:最差值: 1.5888e-185, 最优值: 2.8633e-194, 平均值: 5.6321e-187, 标准差: 0, 秩和检验: 1
GWO:最差值: 0.00089269, 最优值: 1.3208e-09, 平均值: 3.7304e-05, 标准差: 0.00016207, 秩和检验: 3.0199e-11
函数:F5
EEGWO:最差值: 4.0098e-92, 最优值: 6.3481e-97, 平均值: 1.5355e-93, 标准差: 7.3035e-93, 秩和检验: 1
GWO:最差值: 3.3963e-06, 最优值: 1.1332e-07, 平均值: 9.9954e-07, 标准差: 9.3259e-07, 秩和检验: 3.0199e-11
函数:F15
EEGWO:最差值: 2.5597e-96, 最优值: 5.191e-99, 平均值: 3.2324e-97, 标准差: 5.5375e-97, 秩和检验: 1
GWO:最差值: 0.0023484, 最优值: 4.3694e-16, 平均值: 0.0005256, 标准差: 0.00058446, 秩和检验: 3.0199e-11
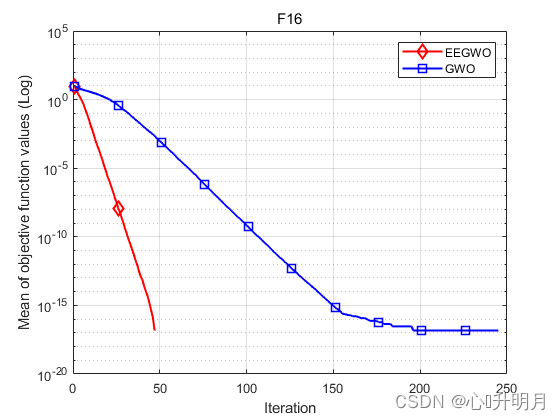
函数:F16
EEGWO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F17
EEGWO:最差值: 1.2875e-188, 最优值: 1.0323e-194, 平均值: 9.4959e-190, 标准差: 0, 秩和检验: 1
GWO:最差值: 4.6298e-07, 最优值: 5.7455e-10, 平均值: 7.9766e-08, 标准差: 1.1157e-07, 秩和检验: 3.0199e-11
实验结果表明:提出的EEGWO算法显著提高了GWO算法的性能。
三、参考文献
[1] Wen Long, Jianjun Jiao, Ximing Liang, et al. An exploration-enhanced grey wolf optimizer to solve high-dimensional numerical optimization[J]. Engineering Applications of Artificial Intelligence, 2018, 63: 63-80.