基于海马优化算法的函数寻优算法
文章目录
- 一、理论基础
-
- 1、海马优化算法
-
- (1)初始化
- (2)海马的移动行为
- (3)海马的捕食行为
- (4)海马的繁殖行为
- 2、SHO算法伪代码
- 二、仿真实验与结果分析
- 三、参考文献
一、理论基础
1、海马优化算法
文献[1]以自然界中海马的运动、捕食和繁殖行为为灵感,提出了一种新的基于群体智能的元启发式算法——海马优化算法(Sea-horse optimizer, SHO)。
(1)初始化
与其他现有的元启发式相似,SHO也从种群初始化开始。设每只海马代表问题搜索空间中的一个候选解,海马的整个种群(简称海马)可表示为: S e a h o r s e s = [ x 1 1 ⋯ x 1 D i m ⋮ ⋱ ⋮ x p o p 1 ⋯ x p o p D i m ] (1) Seahorses=\begin{bmatrix}x_1^1 & \cdots & x_1^{Dim}\\\vdots & \ddots & \vdots\\x_{pop}^1 & \cdots & x_{pop}^{Dim}\end{bmatrix}\tag{1} Seahorses=⎣ ⎡x11⋮xpop1⋯⋱⋯x1Dim⋮xpopDim⎦ ⎤(1)其中, D i m Dim Dim表示变量的维数, p o p pop pop表示种群个体数量。
每个解都是在指定问题的下限和上限之间随机生成的,分别用 L B LB LB和 U B UB UB表示。搜索空间 [ L B , U B ] [LB,UB] [LB,UB]中第 i i i个个体 X i X_i Xi的表达式为: X i = [ x i 1 , … , x i D i m ] x i j = r a n d × ( U B j − L B j ) + L B j (2) \begin{array}{c}X_i=\left[x_i^1,\ldots,x_i^{Dim}\right]\\[2ex]x_i^j=rand\times(UB^j-LB^j)+LB^j\end{array}\tag{2} Xi=[xi1,…,xiDim]xij=rand×(UBj−LBj)+LBj(2)其中, r a n d rand rand表示 [ 0 , 1 ] [0,1] [0,1]中的随机值, x i j x_i^j xij表示第 i i i个个体的第 j j j维, i i i是取值范围为 1 ∼ p o p 1\sim pop 1∼pop的正整数, j j j是取值范围为 [ 1 , D i m ] [1,Dim] [1,Dim]的正整数, L B j LB^j LBj和 U B j UB^j UBj表示优化问题第 j j j个变量的下界和上界。
以最小优化问题为例,将适应度最小的个体视为精英个体,记为 X e l i t e X_{elite} Xelite。 X e l i t e X_{elite} Xelite可由式(3)得到: X e l i t e = a r g m i n ( f ( X i ) ) (3) X_{elite}=argmin(f(X_i))\tag{3} Xelite=argmin(f(Xi))(3)其中, f ( ⋅ ) f(\cdot) f(⋅)为给定问题的目标函数值。
(2)海马的移动行为
对于海马的移动行为,海马的不同运动模式近似服从正态分布 r a n d n ( 0 , 1 ) randn(0,1) randn(0,1)。为了权衡探索和开发的性能,取 r 1 = 0 r_1 = 0 r1=0为分界点,一半用于局部开发,另一半用于全局搜索。所以运动可以分为以下两种情况:
第一种情况:海马的螺旋运动伴随着海洋中的旋涡。当正态随机值 r 1 r_1 r1位于分界点右侧时,它主要实现SHO的局部开发。海马沿着螺旋运动向精英个体 X e l i t e X_{elite} Xelite移动,特别是使用莱维飞行来模拟海马的移动步长,这有利于在迭代早期以较大概率跨越到其他位置的海马,避免了SHO的过度局部开发。同时,海马的这种螺旋移动方式不断改变旋转角度,以扩大现有局部解的邻域。在这种情况下,可以用数学表示,生成海马的新位置如下: X n e w 1 ( t + 1 ) = X i ( t ) + L e v y ( λ ) ( ( X e l i t e ( t ) − X i ( t ) ) × x × y × z + X e l i t e ) (4) X_{new}^1(t+1)=X_i(t)+Levy(\lambda)((X_{elite}(t)-X_i(t))\times x\times y\times z+X_{elite})\tag{4} Xnew1(t+1)=Xi(t)+Levy(λ)((Xelite(t)−Xi(t))×x×y×z+Xelite)(4)其中, x = ρ × cos ( θ ) x=\rho\times\cos(\theta) x=ρ×cos(θ), y = ρ × sin ( θ ) y=\rho\times\sin(\theta) y=ρ×sin(θ)和 z = ρ × θ z=\rho\times\theta z=ρ×θ分别表示螺旋运动下坐标 ( x , y , z ) (x, y, z) (x,y,z)的三维分量,这有利于更新搜索代理的位置; ρ = u × e θ v \rho=u\times e^{\theta v} ρ=u×eθv表示由对数螺旋常数 u u u和 v v v定义的杆的长度(设置 u = 0.05 u=0.05 u=0.05和 v = 0.05 v=0.05 v=0.05); θ \theta θ是 [ 0 , 2 π ] [0,2\pi] [0,2π]之间的随机值; L e v y ( z ) Levy(z) Levy(z)表示莱维飞行分布函数,并且由式(5)计算得到。 L e v y ( z ) = s × w × σ ∣ k ∣ 1 λ (5) Levy(z)=s\times\frac{w\times\sigma}{|k|^{\frac1\lambda}}\tag{5} Levy(z)=s×∣k∣λ1w×σ(5)在式(5)中, λ \lambda λ是 [ 0 , 2 ] [0,2] [0,2]之间的随机数(本文设 λ = 1.5 \lambda = 1.5 λ=1.5), s s s是一个固定常数0.01, w w w和 k k k是[0,1]之间的随机数, σ σ σ由式(6)计算: σ = ( Γ ( 1 + λ ) × sin ( π λ 2 ) Γ ( 1 + λ 2 ) × λ × 2 ( λ − 1 2 ) ) (6) \sigma=\left(\frac{\Gamma(1+\lambda)\times\displaystyle\sin\left(\frac{\pi\lambda}{2}\right)}{\displaystyle\Gamma\left(\frac{1+\lambda}{2}\right)\times\lambda\times2^{\left(\frac{\lambda-1}{2}\right)}}\right)\tag{6} σ=⎝ ⎛Γ(21+λ)×λ×2(2λ−1)Γ(1+λ)×sin(2πλ)⎠ ⎞(6)第二种情况:海马随海浪的布朗运动。在漂移作用下,当 r 1 r_1 r1位于分界点左侧时,进行SHO探索。在这种情况下,搜索操作对于避免SHO的局部极值非常重要。布朗运动用于模拟海马的另一个移动长度,以确保其在搜索空间中更好地探索。这种情况下的数学表达式为: X n e w 1 ( t + 1 ) = X i ( t ) + r a n d ∗ l ∗ β t ∗ ( X i ( t ) − β t ∗ X e l i t e ) (7) X_{new}^1(t+1)=X_i(t)+rand^*l^*{\beta_t}^*\left(X_i(t)-{\beta_t}^*X_{elite}\right)\tag{7} Xnew1(t+1)=Xi(t)+rand∗l∗βt∗(Xi(t)−βt∗Xelite)(7)其中, l l l为常数系数(本文设置 l = 0.05 l=0.05 l=0.05); β t \beta_t βt为布朗运动的随机游走系数,本质上是一个服从标准正态分布的随机值。它可以由式(8)得到。 β t = 1 2 π e x p ( − x 2 2 ) (8) \beta_t=\frac{1}{\sqrt{2\pi}}exp\left(-\frac{x^2}{2}\right)\tag{8} βt=2π1exp(−2x2)(8)综上所述,这两种情况可以得到海马在第 t t t次迭代时的新位置: X n e w 1 ( t + 1 ) = { X i ( t ) + L e v y ( λ ) ( ( X e l i t e ( t ) − X i ( t ) ) × x × y × z + X e l i t e ) r 1 > 0 X i ( t ) + r a n d ∗ l ∗ β t ∗ ( X i ( t ) − β t ∗ X e l i t e ) r 1 ≤ 0 (9) X_{new}^1(t+1)=\begin{dcases}X_i(t)+Levy(\lambda)((X_{elite}(t)-X_i(t))\times x\times y\times z+X_{elite})\quad r_1>0\\[2ex]X_i(t)+rand^*l^*{\beta_t}^*\left(X_i(t)-{\beta_t}^*X_{elite}\right)\quad\quad\quad\quad\quad\quad\quad\quad\quad\, r_1\leq0\end{dcases}\tag{9} Xnew1(t+1)=⎩ ⎨ ⎧Xi(t)+Levy(λ)((Xelite(t)−Xi(t))×x×y×z+Xelite)r1>0Xi(t)+rand∗l∗βt∗(Xi(t)−βt∗Xelite)r1≤0(9)其中, r 1 = r a n d n ( ) r_1=randn() r1=randn()表示标准正态随机数。
(3)海马的捕食行为
海马捕食浮游动物和小型甲壳动物有两种结果:成功和失败。考虑到海马成功捕获食物的概率超过90%,设计SHO的随机数 r 2 r_2 r2来区分这两个结果,并将其设置为临界值0.1。由于精英在一定程度上表示了猎物的大致位置,因此捕食成功强调了SHO的开发能力。如果 r 2 > 0.1 r_2>0.1 r2>0.1,则意味着海马的捕食是成功的,即海马接近猎物(精英),比猎物移动得更快,最终将其捕获。否则,当捕食失败时,两者的响应速度与之前相反,这意味着海马倾向于探索搜索空间。这种捕食行为的数学表达式是: X n e w 2 ( t + 1 ) = { α ∗ ( X e l i t e − r a n d ∗ X n e w 1 ( t ) ) + ( 1 − α ) ∗ X e l i t e i f r 2 > 0.1 ( 1 − α ) ∗ ( X n e w 1 ( t ) − r a n d ∗ X e l i t e ) + α ∗ X n e w 1 ( t ) i f r 2 ≤ 0.1 (10) X_{new}^2(t+1)=\begin{dcases}\alpha^*\left(X_{elite}-rand^*X_{new}^1(t)\right)+(1-\alpha)^*X_{elite}\quad\quad if\,\,r_2>0.1\\[2ex](1-\alpha)^*\left(X_{new}^1(t)-rand^*X_{elite}\right)+\alpha^*X_{new}^1(t)\quad if\,\,r_2\leq0.1\end{dcases}\tag{10} Xnew2(t+1)=⎩ ⎨ ⎧α∗(Xelite−rand∗Xnew1(t))+(1−α)∗Xeliteifr2>0.1(1−α)∗(Xnew1(t)−rand∗Xelite)+α∗Xnew1(t)ifr2≤0.1(10)其中, X n e w 1 ( t ) X_{new}^1(t) Xnew1(t)表示海马在迭第 t t t次迭代时移动后的新位置; r 2 r_2 r2是 [ 0 , 1 ] [0,1] [0,1]之间的随机数; α \alpha α随迭代线性减小,以调整海马捕食时的移动步长,由式(11)计算。 α = ( 1 − t T ) 2 t T (11) \alpha=\left(1-\frac tT\right)^{\frac{2t}{T}}\tag{11} α=(1−Tt)T2t(11)其中, T T T表示最大迭代次数。
(4)海马的繁殖行为
根据适应度值,种群被分为雄性和雌性群体。由于雄性海马负责繁殖,SHO算法将具有最佳适应度值的一半个体作为父体,另一半作为母体。这种划分将有利于父体和母体之间继承好的特征,以培养下一代,并避免新解决方案的过度局部化。海马角色分配的数学表达式为: f a t h e r s = X s o r t 2 ( 1 : p o p / 2 ) m o t h e r s = X s o r t 2 ( p o p / 2 + 1 : p o p ) (12) \begin{array}{c}fathers=X_{sort}^2(1:pop/2)\\[2ex]mothers=X_{sort}^2(pop/2+1:pop)\end{array}\tag{12} fathers=Xsort2(1:pop/2)mothers=Xsort2(pop/2+1:pop)(12)其中, X s o r t 2 X_{sort}^2 Xsort2表示所有 X n e w 2 X_{new}^2 Xnew2按适应度值升序排列, f a t h e r s fathers fathers和 m o t h e r s mothers mothers分别来自雄性和雌性群体。
雄性和雌性随机交配产生新的后代。为了使所提出的SHO算法易于执行,假设每对海马只繁殖一个后代。第 i i i个子代的表达式如下: X i o f f s p r i n g = r 3 X i f a t h e r + ( 1 − r 3 ) X i m o t h e r (13) X_i^{offspring}=r_3X_i^{father}+(1-r_3)X_i^{mother}\tag{13} Xioffspring=r3Xifather+(1−r3)Ximother(13)其中, r 3 r_3 r3是 [ 0 , 1 ] [0,1] [0,1]之间的随机数, i i i是 [ 1 , p o p / 2 ] [1,pop/2] [1,pop/2]范围内的正整数, X f a t h e r X^{father} Xfather和 X m o t h e r X^{mother} Xmother分别表示从雄性和雌性群体中随机选择的个体。
2、SHO算法伪代码
二、仿真实验与结果分析
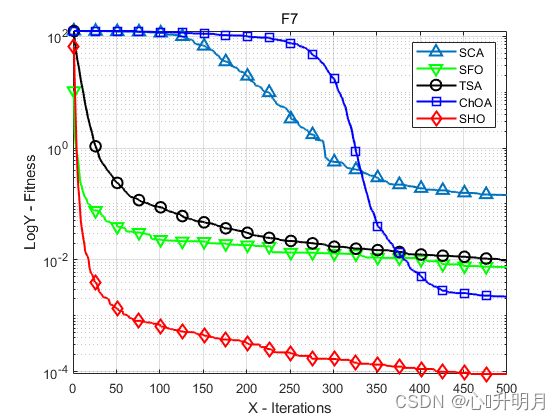
将SHO与SCA、SFO、TSA和ChOA进行对比,以文献[1]中表2~表4的F3、F5、F7(单峰函数/30维)、F10、F11、F12(多峰函数/30维)、F15、F16、F18(固定维度多峰函数/4维、2维、2维)为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:







函数:F3
SCA:最差值: 18368.1464, 最优值: 381.1087, 平均值: 8870.2067, 标准差: 5411.8773, 秩和检验: 3.0199e-11
SFO:最差值: 7759.311, 最优值: 6.8185, 平均值: 1761.5799, 标准差: 1924.3401, 秩和检验: 3.0199e-11
TSA:最差值: 0.0055186, 最优值: 3.8235e-09, 平均值: 0.00039452, 标准差: 0.0011145, 秩和检验: 3.0199e-11
ChOA:最差值: 595.7466, 最优值: 0.33056, 平均值: 78.0833, 标准差: 147.4911, 秩和检验: 3.0199e-11
SHO:最差值: 1.1809e-96, 最优值: 9.2915e-109, 平均值: 4.1727e-98, 标准差: 2.1545e-97, 秩和检验: 1
函数:F5
SCA:最差值: 1843098.6418, 最优值: 29.1753, 平均值: 133966.1289, 标准差: 354304.683, 秩和检验: 3.0199e-11
SFO:最差值: 3070.9505, 最优值: 13.8042, 平均值: 197.8938, 标准差: 549.5994, 秩和检验: 3.6459e-08
TSA:最差值: 29.745, 最优值: 26.0271, 平均值: 28.5275, 标准差: 0.7178, 秩和检验: 0.053685
ChOA:最差值: 28.9706, 最优值: 27.383, 平均值: 28.8451, 标准差: 0.3209, 秩和检验: 7.1186e-09
SHO:最差值: 28.8602, 最优值: 27.2442, 平均值: 28.2633, 标准差: 0.45871, 秩和检验: 1
函数:F7
SCA:最差值: 0.80374, 最优值: 0.0032941, 平均值: 0.14467, 标准差: 0.17658, 秩和检验: 3.0199e-11
SFO:最差值: 0.036979, 最优值: 0.00029887, 平均值: 0.0074278, 标准差: 0.0090561, 秩和检验: 3.0199e-11
TSA:最差值: 0.022183, 最优值: 0.0026778, 平均值: 0.0096315, 标准差: 0.0049444, 秩和检验: 3.0199e-11
ChOA:最差值: 0.0066974, 最优值: 0.00012385, 平均值: 0.0021978, 标准差: 0.0021073, 秩和检验: 1.0937e-10
SHO:最差值: 0.00027927, 最优值: 6.3171e-06, 平均值: 9.0713e-05, 标准差: 7.2435e-05, 秩和检验: 1
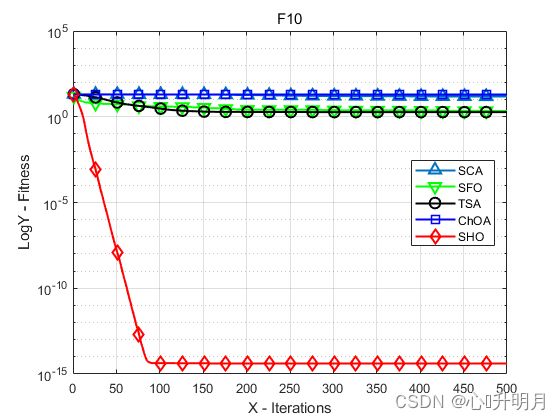
函数:F10
SCA:最差值: 20.3208, 最优值: 0.045212, 平均值: 15.1075, 标准差: 8.164, 秩和检验: 3.1507e-12
SFO:最差值: 4.0537, 最优值: 0.13557, 平均值: 2.1672, 标准差: 1.2368, 秩和检验: 3.1507e-12
TSA:最差值: 20.1429, 最优值: 2.9496e-12, 平均值: 1.8574, 标准差: 3.7532, 秩和检验: 3.1507e-12
ChOA:最差值: 19.9644, 最优值: 19.9597, 平均值: 19.9626, 标准差: 0.0011774, 秩和检验: 3.1507e-12
SHO:最差值: 4.4409e-15, 最优值: 8.8818e-16, 平均值: 4.0856e-15, 标准差: 1.084e-15, 秩和检验: 1
函数:F11
SCA:最差值: 1.8531, 最优值: 0.14491, 平均值: 0.95115, 标准差: 0.28752, 秩和检验: 1.7203e-12
SFO:最差值: 3.1087, 最优值: 0.36601, 平均值: 1.3575, 标准差: 0.55987, 秩和检验: 1.7203e-12
TSA:最差值: 0.024404, 最优值: 0, 平均值: 0.0070767, 标准差: 0.0086288, 秩和检验: 5.6652e-05
ChOA:最差值: 0.115, 最优值: 1.9304e-10, 平均值: 0.015874, 标准差: 0.032814, 秩和检验: 2.6819e-11
SHO:最差值: 0.031959, 最优值: 0, 平均值: 0.0010653, 标准差: 0.0058349, 秩和检验: 1
函数:F12
SCA:最差值: 244166.8628, 最优值: 0.97179, 平均值: 9929.5975, 标准差: 44561.5225, 秩和检验: 3.0199e-11
SFO:最差值: 0.59784, 最优值: 0.006079, 平均值: 0.16892, 标准差: 0.13795, 秩和检验: 0.00028389
TSA:最差值: 23.2113, 最优值: 0.81292, 平均值: 8.3327, 标准差: 5.1493, 秩和检验: 3.0199e-11
ChOA:最差值: 0.89046, 最优值: 0.23538, 平均值: 0.44436, 标准差: 0.15671, 秩和检验: 1.8608e-06
SHO:最差值: 0.71867, 最优值: 0.090756, 平均值: 0.2777, 标准差: 0.14157, 秩和检验: 1
函数:F15
SCA:最差值: 0.0016268, 最优值: 0.00041092, 平均值: 0.0010905, 标准差: 0.0003873, 秩和检验: 1.0105e-08
SFO:最差值: 0.0028866, 最优值: 0.00031332, 平均值: 0.0013138, 标准差: 0.00084783, 秩和检验: 4.6856e-08
TSA:最差值: 0.11711, 最优值: 0.00030772, 平均值: 0.014668, 标准差: 0.026132, 秩和检验: 0.016955
ChOA:最差值: 0.0013775, 最优值: 0.0012251, 平均值: 0.0012877, 标准差: 4.1797e-05, 秩和检验: 8.4848e-09
SHO:最差值: 0.0016193, 最优值: 0.00030868, 平均值: 0.00043028, 标准差: 0.00032552, 秩和检验: 1
函数:F16
SCA:最差值: -1.0315, 最优值: -1.0316, 平均值: -1.0316, 标准差: 2.4636e-05, 秩和检验: 3.0199e-11
SFO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 2.8474e-07, 秩和检验: 2.6695e-09
TSA:最差值: -1, 最优值: -1.0316, 平均值: -1.0295, 标准差: 0.0080246, 秩和检验: 4.9752e-11
ChOA:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 9.9195e-06, 秩和检验: 3.0199e-11
SHO:最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 8.6802e-09, 秩和检验: 1
函数:F18
SCA:最差值: 3.0007, 最优值: 3, 平均值: 3.0001, 标准差: 0.00014316, 秩和检验: 3.0199e-11
SFO:最差值: 3.0001, 最优值: 3, 平均值: 3, 标准差: 1.428e-05, 秩和检验: 3.0199e-11
TSA:最差值: 84.0004, 最优值: 3, 平均值: 14.7022, 标准差: 25.2511, 秩和检验: 3.0199e-11
ChOA:最差值: 3.0006, 最优值: 3, 平均值: 3.0002, 标准差: 0.00016064, 秩和检验: 3.0199e-11
SHO:最差值: 3, 最优值: 3, 平均值: 3, 标准差: 6.5399e-09, 秩和检验: 1
实验结果表明:SHO算法在7个单峰函数和大部分多峰函数上都明显优于4种最先进的比较算法。
三、参考文献
[1] Shijie Zhao, Tianran Zhang, Shilin Ma, et al. Sea-horse optimizer: a novel nature-inspired meta-heuristic for global optimization problems[J]. Applied Intelligence, 2022.
