【论文精读与思考】：深度强化学习的组合优化研究进展

论文来源基本信息

• 作者：李凯文、张涛、王锐等
• 作者单位：国防科技大学
• 期刊：自动化学报
• 时间：2021年11月组合优化问题
• 链接：基于深度强化学习的组合优化研究进展 (aas.net.cn)

1 组合优化问题概述

1.1 定义

一类在离散状态下求极值的最优化问题，数学模型：
$$\begin{gathered} minF(x) \\ s.t.G(x)\ge 0 \\ x\in D \end{gathered}$$
其中x为决策变量，F(x)为目标函数，G(x)为约束条件，D表示离散的决策空间。

1.2 特点

其决策空间为有限点集，直观上可以通过穷举法得到问题的最优解，但是由于可行解数量随问题规模呈指数型增长, 无法在多项式时间内穷举得到问题的最优解。

1.3 求解方法

1.3.1 精确方法

• 常用的方法：分支定界法、动态规划法
• 优点：可以求解得到问题的全局最优解
• 缺点：问题规模扩大时，会消耗巨大的计算量。

1.3.2 近似方法

• 常用的方法：近似算法和启发式算法
• 近似算法：可以得到有质量的解，如贪心算法、线性规划、局部搜索算法等
• 启发式算法：利用设定的启发式规则对解空间进行搜索，例如模拟退火算法、遗传算法、蚁群算法、差分进化算法、粒子群算法、变邻域搜索、基于群体智能算法的进化算法等
• 优点：在可接受的时间内搜索得到一个较好的解
• 缺点：很难拓展到在线、实时优化问题

1.4 应用

组合优化问题在国防、交通、智能制造、优化决策、电力、通信等领域都有应用，常见问题有：

• 旅行商问题 TSP
• 车辆路径问题 VRP
• 车间作业调度问题
• 背包问题
• 最小顶点覆盖问题 MVC
• 最小支配集问题 MDP

2 深度强化学习（DRL）解决组合优化问题的概述

2.1 二者联系

• 深度强化学习：根据当前环境做动作选择，并根据动作反馈不断调整自身的策略
• 组合优化：在离散决策空间内进行决策变量的最优选择
• 组合优化“选择决策变量”与深度强化学习的“动作选择”很相似
• 优势：DRL“离线训练、在线决策”的特性可以解决组合优化中的“实时求解”问题

2.2 目前主要方法

2.2.1 基于DRL的端到端方法

具体方法介绍见第3章

• 定义：给定问题实例作为输入，利用训练好的深度神经网络直接输出问题的解。网络参数由DRL方法训练得到。
• 优势：该方法求解速度块，模型训练完成后有普适性和很强的泛化能力。
• 劣势：神经网络的”不确定性“懂得都懂，解的最优性很难保证，并且在中大规模问题上求解能力与LKH3、Google OR tools等求解器有一定差距。

2.2.2 基于DRL改进的传统方法

本文不过多赘述此方面的内容

• 利用机器学习模型对分支定界法的节点选择和变量选择策略进行优化

2.2.3 基于DRL的局部搜索改进方法

• 利用深度强化学习对解搜索的启发式规则进行学习和选择，通过学习到的启发式规则进行学习和选择
• 优势：具有较好的优化效果
• 劣势：本质上还是迭代型搜索算法，求解速度不如端到端方法

3 基于DRL的端到端方法

分类：基于Pointer network的端到端方法、基于图神经网络的端到端方法

3.1 基于Pointer netword的端到端方法

3.1.1 方法原理

1. 方法概括：利用神经网络模型实现序列到序列的映射。
2. 核心思想：利用编码器 (Encoder) 对组合优化问题的输入序列进行编码得到特征向量, 再利用解码器 (Decoder) 结合Attention注意力机制计算方法以自回归的方式逐步构造解, 自回归即每次选择一个节点, 并在已选择节点的基础上选择下一个节点, 直到构造得到完整解。

3.1.2 举例：经典指针网络模型求解TSP问题

1. 经典指针网络模型的编码器和解码器都是LSTM循环神经网络

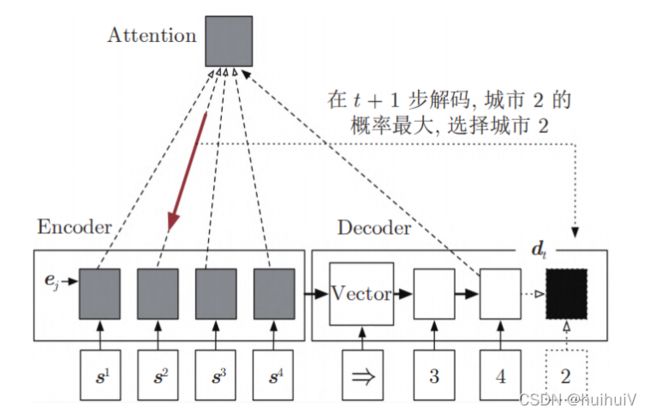
2. 如下图所示构建TSP解：

   （1）编码过程：输入每个城市的二维坐标转换成高维节点的表征向量s_i,编码器LSTM读入s_i,得到一个存储输入序列的向量Vector，同时LSTM得到每个城市的隐层状态e_j。

   （2）解码过程：t=0时第一次解码LSTM读入Vector，输出当前隐层状态d₀,利用Attention机制计算选择各个城市的概率，此时可以选择概率最大的节点作为第一次选择的城市。然后继续解码t=1时LSTM读入上一步LSTM的隐层输出和上一步选择城市的特征向量，输出当前的隐层状态d₁，根据d₁和各城市的e_j计算各个城市的概率，之后以此类推计算t=n时的情况，计算公式见(3-1)，即Attention机制：
   $$\begin{array}{r}{u}_j^t={\mathbf{v}}^{\mathrm{T}}\tanh \left({\mathbf{W}}_1{\mathbf{e}}_j+{\mathbf{W}}_2{\mathbf{d}}_t\right),j\in (1,\cdots ,n)\\ P\left({\rho }_{t+1}\mid {\rho }_1,\cdots ,{\rho }_t,X_t\right)=\mathrm{softmax}\left({\mathbf{u}}^t\right)\end{array}\text{\hspace{1em}(3-1)}$$
   （3）本质上来说就是利用当前的d_t值和各个城市的隐层状态e_j计算得到第t步选择各城市的概率，其中W和v都是神经网络里面的参数，$u_j^i$代表在第t步解码过程中选择城市j的概率。

3. 总结：通过不断把具有最大概率值的节点添加到解当中，按照该方式不断选择城市，直至构造一个完整解。该深度神经网络模型的输入：城市的坐标序列；输出：城市的顺序。

   Softmax函数：

   1. 目的：将实数范围内的分类结果转化为0-1之间的概率数值。

   2. 方法：

   （1）用指数的特性，将实数映射到0-正无穷（非负）

   （2）利用归一化方法，将1.的结果转化为0-1之间的概率。

3.1.3 强化学习训练方法

1. 建模：将组合优化问题建模为马尔科夫决策过程。下面以TSP为例：

   • 状态：城市t的坐标与已访问过的城市
   • 动作：第t步选择的城市t
   • 奖励函数：路径总距离的相反数-L(π)

2. 策略：通常为随机策略，即选择城市的概率。例如可以确定每一步动作的概率来计算下一个访问城市的概率，根据链式法则累乘就可以得到城市坐标到最终访问顺序的映射。策略由神经网络参数θ进行参数化。根据公式(3-2)进行更新：
   $$\begin{array}{l}\nabla \mathcal{L}(\theta \mid s)=\\ {\mathrm{E}}_{{\mathrm{p}}_{\theta }(\pi \mid \mathrm{s})}\left[(L(\pi )-b(s))\nabla \ln p_{\theta }(\pi \mid s)\right]\\ \theta \leftarrow \theta +\nabla \mathcal{L}(\theta \mid s)\end{array}\text{\hspace{1em}(3-2)}$$
   $ln{p}_{\theta }(\pi \mid s)$ 计算每步动作选择概率对数的求和，以该值对参数计算偏导就可以得到梯度值$\nabla \ln p_{\theta}(\pi \mid s) $ ,$L(\pi )-b(s)$ 决定了梯度下降的方向，如果当前表现比"平均表现b(s)"好的话，那么就对该策略正向激励。那么b(s)的由来有很多方法，比较常用的话就是加一个Critic网络，类似AC结构。

3.1.4 方法综述/研究进展

1. 开山之作：Vinyals等在2015年提出了Pointer network模型进行组合优化问题求解，这篇文章的详细原理在3.1.2已经介绍。这篇文章实现了对50个城市的小规模TSP问题的快速求解。但是在文章中作者采用的是监督学习的方式，预先需要构造大量样本来进行预训练，也决定了解的质量很难超过样本解的质量。

2. 引入强化学习训练：Bello等采用强化学习训练上述模型，并且引入了Critic网络作为Baseline降低训练方差。文章对100个城市的TSP问题进行测试，解的质量超过了Vinyals的监督模型，并解决了背包问题。

3. 借鉴Transformer模型：

   （1）旧瓶新装：仍是Pointer Network模型，采用了与Transformer模型编码层相同的结构，利用Multi-head attention方法计算得到节点的特征向量（Deudon等）

   （2）新瓶新装：利用Attention机制提出新模型（Kool提出CVRP模型）

4. 结合图神经网络：Ma等设计图指针网络，通过“指针网络对城市坐标线性映射，得到点嵌入”+“GNN图神经网络对所有城市编码，得到每个城市的图嵌入”一共两种编码方式，然后基于Attention机制去计算城市选择的概率，再使用分层强化学习(HRL)进行训练，在500-1000的大规模TSP问题上达到了Sota效果。

5. 研究侧重点：指针网络模型利用Attention机制以自回归的方式对解继续了构造，比较适合求解有序列组合优化问题，比如TSP、VRP问题。

3.2 基于图神经网络的端到端方法

3.1.1 方法原理

1.核心思想：根据每个节点的原始信息 (如城市坐标) 和各个节点之间的关系 (如城市之间的距离), 利用图神经网络方法计算得到各个节点的特征向量, 根据各个节点的特征向量进行节点预测、边预测等任务。

2.相关定义：图定义为G=（V,E），V代表节点的集合，E为边的集合。

3.1.2 举例：经典的GNN模型

各个节点的表征如公式(3-3)更新：
$$h_v^{(t)}=\sum _{u\in N(v)}f\left({\mathbf{x}}_v,{\mathbf{x}}_{(v,u)}^e,{\mathbf{x}}_u,h_u^{(t-1)}\right)\text{\hspace{1em}(3-3)}$$
$h_v^{(t)}$ 代表节点v的表征向量，N(v)代表v的相邻节点的集合，$x_v$是节点v的特征，$x_{(v,u)}^e$ 是与v相连的边的特征，$x_u$是相邻节点u的特征。该公式的更新方式就是根据节点自身特征、边特征以及邻居节点的特征对节点v的表征向量进行更新，一直到该节点表征向量收敛为止，从而得到准确的特征向量。

3.1.3 如何应用在组合优化问题上？

1. 最小顶点覆盖问题（节点选择）:可以将图神经网络得到的$h_v^{(t)}$以一个全连接层神经网络映射到节点选择概率，从而根据概率进行节点的选择。

2. TSP问题（边选择）：以两个节点的特征向量作为输入，以一个全连接层神经网络映射得到一个选择概率。但是可能不一定能构成一个完整的回路，因此有时需要辅以一些搜索方法。

3.1.4 方法综述/研究进展

1. 开山之作：Dai等使用 structure2vec 图神经网络建模,并基于贪婪策略根据图神经网络计算剩余可选节点中各个节点的Q值, 从而选择一个新的节点添加到当前解中，直至得到完整解。采用DQN算法对参数进行训练，使得模型输出准确的Q值，算法结果在TSP问题上取得了接近3.1.4中Bello等的方法效果。
2. 网络的改进：Mittal把使用的图神经网络改成了GCN建模，实验结果发现在处理20k-50k的大规模组合优化问题上比Dai的模型获得了41％的提升。
3. 研究侧重点：图神经网络可以计算得到节点选择概率，因此主要应用在无关节点顺序选择的问题上，如MVC（最小顶点覆盖）、MIS（最大独立点集）等。如果要研究TSP问题的话，主要方法可以以自回归方式逐步选择节点或者结合波束搜索等。

4 基于DRL的局部搜索改进算法与多目标组合优化方法

4.1 基于DRL的局部搜索改进算法

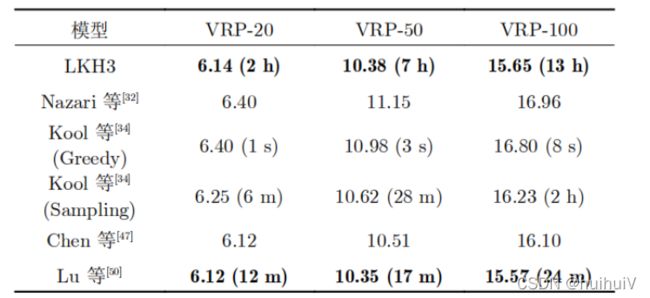
深度强化学习改进的局部搜索方法是自2019年以来最新提出的一类组合优化方法, 主要用于求解VRP等路径优化问题，从下列实验对比中可以看出在效果上优于当前性能最好的端到端模型，甚至优于LKH3等专业组合优化求解器，但是运行时间相较于端对端模型会大大增加。

1. 开山之作：Chen等提出基于深度强化学习的组合优化问题搜索模型，利用AC网络对局部搜索的策略进行训练，利用学习到的策略对搜索过程引导。文章实验的优化效果在车间作业调度和TSP问题上超越了Google OR-tools求解器。
2. 借鉴探索与平衡：Lu等在2020年提出一种LSI算法。算法的创新在于引入了两个算子：提升算子和扰动算子。在每一步搜索的过程中都要决定是继续提升当前解还是扰动当前解（个人感觉类似于探索和利用的平衡）。利用DRL去训练提升算子的选择策略，当取得局部最优就进行扰动，向下一个局部区域探索。实验结果超越了LKH3算法的性能，并大幅减少时间。

4.2 基于DRL的多目标组合优化方法

“多目标深度强化学习”的概念很早就被提出并且存在很多文献对其进行研究, 但是其研究的是如何设计具有多个奖励信号的强化学习算法, 例如如何利用强化学习算法控制潜艇寻找目标,其中需要最大化寻找到目标的数量和最小化寻找的时间, 其研究的主体是多目标强化学习算法, 而不是如何利用强化学习方法解决传统的多目标优化问题。

Li等提出了采用基于分解的思想将多目标问题分解为多个子问题，并将每个子问题建模为Pointer Network模型，多个子模型利用基于邻居的参数迁移的方法进行协同训练。该方法在2、3、5个目标的TSP问题上取得了优于传统NSGA-II多目标优化算法的优化效果，而且具有很强的泛化能力以及较快的求解速度。

在该方向上的研究较少，或许可以作为一个深入研究的方向。

5 方法总结

从上述方法可见, 端到端模型具有求解速度远超传统优化算法的优势, 也是近年来研究较多的一类方法, 模型一旦训练完成, 可以对任意同类型的问题进行求解, 具有很强的泛化能力, 但是很难保证解的优化效果, 尤其随着问题规模的扩大, 其优化能力与传统优化算法之间的差距会不断扩大。深度强化学习改进的局部搜索方法是近年来兴起的另外一类方法, 其本质上仍然是启发式搜索算法, 但是没有采用人工设计的搜索规则, 而是利用深度强化学习算法对搜索规则进行学习, 因此该方法具有较强的优化能力, 其优化效果可以超越传统的优化算法, 但是其求解时间仍然远慢于端到端模型, 因此决策者需要根据优化效果和求解速度之间的权衡来选择不同的方法。

由于端到端模型可以采用监督式和强化学习方法进行训练, 这两种方法中，强化学习训练方法收敛比监督式训练方法慢, 但强化学习得到的模型具有更强的泛化能力。

近年来图神经网络结合各种搜索方法 (波束搜索、树搜索) 在各种组合优化问题上得到了广泛的应用, 其主要应用于没有序列特性的组合优化问题, 如MVC、MIS等。而基于 Attention 机制的指针网络方法是解决具有序列决策特性组合优化问题的主要方法, 如 TSP、VRP 等问题。

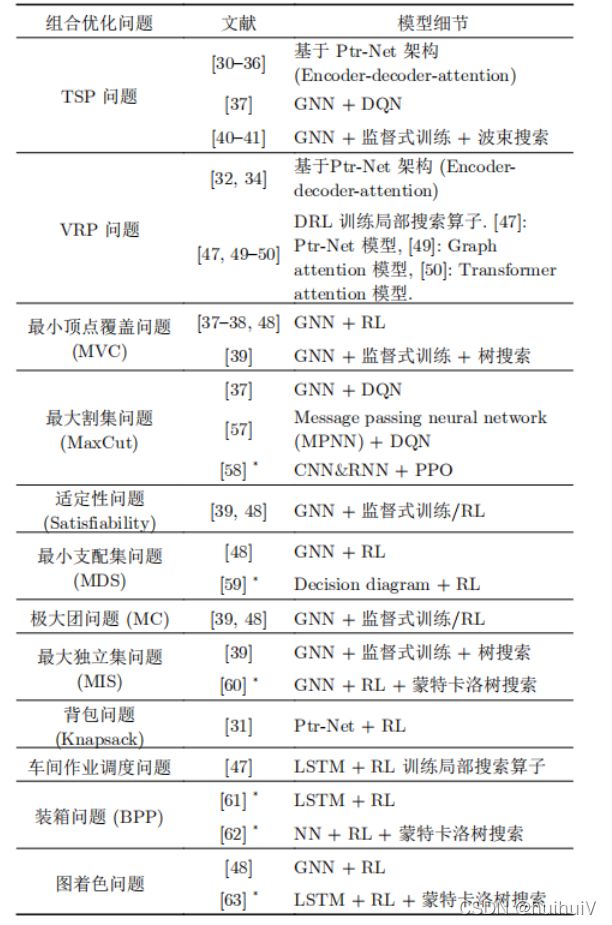
下表主要罗列文章中不同组合优化问题的求解算法统计与比较。

6 应用综述

组合优化问题广泛存在于工业、制造、通信、交通等各个领域, 随着在各个领域中实际问题规模的不断扩大以及对算法求解时间的严格要求, 传统运筹优化方法很难在可接受时间内实现问题的在线求解, 基于深度强化学习的组合优化方法作为近年来提出的一类前沿方法, 具有求解速度快、泛化能力强的优势。

6.1 网络与通信领域

由于网络与通信领域存在多种典型的组合优化问题, 如资源分配、路由拓扑优化等, 因此基于深度强化学习的组合优化在网络与通信领域存在较多的应用。

6.1.1 资源分配

资源分配问题是指将有限的CPU、内存、带宽等资源分配给不同的用户或任务需求, 如虚拟网络功能部署问题、网络资源切片问题等。

6.1.2 拓扑与路由优化

在通信网络或者无线传感网络中, 通常需要对路由策略、传感器的连接拓扑进行优化, 以降低通信时延和成本。

6.1.3 计算迁移

计算迁移是通过将部分计算任务从本地迁移到远程设备以解决移动终端资源受限问题的一个有效途径, 由于无线信道状况变化较快, 需要快速进行策略相应, 而传统的数值优化方法很难实现在线快速优化, 因此需要深度强化学习的在线优化。

6.2 交通领域

1. 在货物配送领域, 随着电商规模的不断扩大,当前的配送路径优化方法很难做到城际交通规划系统的在线实时响应。
2. 在网约车领域，订单的分配和司机载客区域的分配是一个复杂的组合优化问题，传统运筹优化方法很难处理大规模订单的在线调度和响应。
3. 交通信号灯控制

6.3 生产制造领域

1.流水车间调度问题

2.置换车间工作流调度问题

3.机器人制造零件排序问题

6.4 高性能计算领域

人工智能模型的训练是一个耗时极长的任务,合理地对计算资源进行规划和调度能够有效提高计算效率, 随着神经网络规模的不断扩大, 多CPU和多GPU混合训练是当前通用的一个方法, 将神经网络模型的不同计算功能部署在不同的计算设备上对训练速度有很大的影响。

6.5 微电网能量管理领域

在微电网能量管理问题中, 用电、储能等设备的启停控制是典型的离散优化问题。

6.6 问题与展望

1. 在模型方面：在当前的研究中, 直接采用深度神经网络模型输出的解通常较差, 大部分文献都需要进一步通过波束搜索、局部搜索、采样策略等方式进一步提升解的质量, 这说明当前的模型仍然有很大的提升空间, 未来需要进一步对求解组合优化问题的深度神经网络模型进行研究, 如何有效结合图神经网络和 Attention 机制是一个较好的研究点。

2. 在研究对象方面：当前文献研究的问题都相对简单, 而实际中的组合优化问题通常具有多目标、多约束、非静态等复杂特性, 当前方法很难对该类问题进行求解, 目前考虑多目标优化、约束优化的文章较少。未来基于深度强化学习方法对多目标、约束优化、动态优化问题进行研究是一个重要的研究方向。

3. 在深度强化学习训练算法方面：目前对端到端模型的训练大多采用DQN 等传统训练算法, 具有采样效率低、收敛慢等缺陷, 如何根据组合优化问题的特性设计更加高效的强化学习训练算法也是一个未来需要着重研究的内容。

4. 如何利用基于深度强化学习的组合优化方法来解决工程实际中的在线调度优化问题将会成为未来重要的研究方向。

一点思考

在各个领域有很多的组合优化问题，在强化学习里面有很多不同的深度强化学习算法。特别是针对不同领域的组合优化问题结合上具体的约束条件，会有很多不一样的建模。算法亦是如此，针对不同的问题以及不同的研究目标，那么状态、动作、奖励函数的设计都可以发生一定改变，策略也可以因此改进。

强化学习在解决单目标的问题上已经崭露头角，但是多目标问题交给强化学习来解决还是有些吃力，接下来可以的话往多目标组合优化问题去探索或许会是一个不错的选择。