机器学习实战10-Artificial Neural Networks人工神经网络简介(mnist数据集)

目录

一、感知器

1.1、单层感知器

1.2、多层感知器MLP与反向传播

二、用 TensorFlow 高级 API 训练 MLP

DNNClassifier（深度神经网络分类器）

2.1、初始化：

2.2、方法（Methods）

2.2.1、训练train：

2.2.2、evaluate（评估）

2.2.3、predict（预测）

三、使用普通 TensorFlow 训练 DNN

3.1、构建阶段

3.2、执行阶段

3.3、Tensorboard可视化 

四、微调神经网络超参数

4.1隐藏层数量

4.2、每层隐藏层的神经元数量

4.3、激活函数

---

一、感知器

1.1、单层感知器

       是SVM和Neural Network的基础。Perceptron是一个线性分类器，基于误分类准则学习分离超平面的参数(w, b).通过对偶学习法的推导可以通过运用核技巧使Perceptron可以分类非线性数据。

       感知器是最简单的人工神经网络结构之一,它是基于一种稍微不同的人工神经元，称为线性阈值单元（LTU）：输入和输出现在是数字，并且每个输入连接都与权重相连。LTU计算其输入的加权和，然后将阶跃函数应用于该加权和，并输出结果：

                                          

最常见的在感知器中使用的阶跃函数是Heaviside阶跃函数。有时使用符号函数代替。

                               

       感知器简单地由一层 LTU 组成，每个神经元连接到所有输入。此外，通常添加额外偏置特征（X0=1）。这种偏置特性通常用一种称为偏置神经元的特殊类型的神经元来表示，它总是输出 1。下图表示具有两个输入和三个输出的感知器。该感知器可以将实例同时分类为三个不同的二进制类，这使得它是一个多输出分类器。

                               

感知器的表达能力

      学习一个感知器意味着选择权重w0,......wn的值。我们可以把感知器看作n维实例空间中的超平面决策面。对于超平面一侧的实例，感知器输出1，对于另一侧的实例输出-1，如下图所示。这个决策超平面方程是。当然，某些正反样例集合不可能被任一超平面分割。那些可以被分割的成为线性可分（linearly separable）的样例集合。

                                                     

感知器如何训练？

   超平面可用如下方程来描述：

                                                  

  一个点距离超平面的距离d的大小可以表示分类预测的确信程度。在超平面确定的情况下，

                                                                

    函数间隔(wx+b) 实际上就是|f(x)|，几何间隔就是函数间隔除以||w||，才是直观上的点到超平面的距离。当||w||=1的时候，无论扩大几倍，对距离都没有影响，这叫做几何距离。

将误分类点到分离超平面距离作为损失函数：

                                      

该损失函数是(w, b)的连续可导函数，可以通过优化算法求解最优参数，学习的目标是：

                                     

Perceptron采用随机梯度下降来学习参数(w, b)：

首先选取任意的，选取一个误分类点,计算损失函数对(w, b)的导数

                                                

然后更新当前的(w, b)

                                         

一直循环直至没有误分类点，得到参数最优解.

可以将Perceptron认为一个两层的神经网络，输入层是向量x，输出层是一个激活函数为的节点。

from：https://www.jianshu.com/p/a66591fa0bad

    Donald Hebb 提出，当一个生物神经元经常触发另一个神经元时，这两个神经元之间的联系就会变得更强。这个规则后来被称为 Hebb 规则；也就是说，当两个神经元具有相同的输出时，它们之间的连接权重就会增加。使用这个规则的变体来训练感知器。更具体地，感知器一次被馈送一个训练实例，并且对于每个实例，它进行预测。对于每一个产生错误预测的输出神经元，它加强了输入的连接权重，这将有助于正确的预测。

                                   

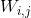
1. 其中是第i输入神经元与第j个输出神经元之间的连接权重。
2. xi是当前训练实例的输入值。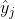
3. 是当前训练实例的第j个输出神经元的输出。
4. 是当前训练实例的第j个输出神经元的目标输出。
5. 是学习率。

        对于权值的调整是一例一调，也就是输入一个样例，就来调整W的值，一直训练到会收敛到一个能正确分类所有训练样例的权向量，前提是训练样例线性可分，并且使用了充分小的η 。如果数据不是线性可分的，那么不能保证收敛。

      每个输出神经元的决策边界是线性的，因此感知机不能学习复杂的模式（就像 Logistic 回归分类器）。然而如果训练实例是线性可分离的，该算法将收敛到一个解。这被称为感知器收敛定理。sklearn 提供了一个感知器类，它实现了一个LTU网络。它可以像你所期望的那样使用，例如在 iris 数据集：

import numpy as np 
from sklearn.datasets import load_iris 
from sklearn.linear_model import Perceptron
iris = load_iris() 
X = iris.data[:, (2, 3)]  # 花瓣长度，宽度 
y = (iris.target == 0).astype(np.int) 
per_clf = Perceptron(random_state=42) 
per_clf.fit(X, y)
per_clf.predict([[2, 0.5]]) 

感知器学习算法类似于随机梯度下降。事实上，sklearn 的感知器类相当于使用具有以下超参数的 SGD 分类器：loss="perceptron"，learning_rate="constant"（学习率），eta0=1，penalty=None（无正则化）。

SGDClassicifer官方文档：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDClassifier.html

注意，与逻辑回归分类器相反，感知机不输出类概率，而是基于硬阈值进行预测.

1.2、多层感知器MLP与反向传播

     MLP 由一个输入层、一个或多个称为隐藏层的 LTU 组成，一个最终层 LTU 称为输出层。除了输出层之外的每一层包括偏置神经元，并且全连接到下一层。当人工神经网络有两个或多个隐含层时，称为深度神经网络（DNN）。

                                                  

反向传播:

     对于每个训练实例，算法将其馈送到网络并计算每个连续层中的每个神经元的输出（向前传递）。然后测量网络的输出误差（即，期望输出和网络实际输出之间的差值），并且计算最后隐藏层中的每个神经元对每个输出神经元的误差贡献多少。然后继续测量这些误差贡献有多少来自先前隐藏层中的每个神经元等等，直到算法到达输入层。该反向传播能够有效地测量网络中所有连接权重的误差梯度，通过在网络中向后传播误差梯度。

     简短来说：对于每个训练实例，反向传播算法首先进行预测（前向），测量误差，然后反向遍历每个层来测量每个连接（反向传递）的误差贡献，最后稍微调整连接器权值以减少误差（梯度下降步长）。

         为了使算法能够正常工作，用 Logistic 函数代替了阶跃函数，σ(z)=1/(1+exp(-z))。因为阶跃函数只包含平坦的段，没有梯度来工作（梯度下降不能在平面上移动），而 Logistic 函数到处都有一个定义良好的非零导数，允许梯度下降在每个步上取得一些进展。反向传播算法可以与其他激活函数一起使用，而不是 Logistic 函数。另外两个流行的激活函数是：

双曲正切函数:

                                                 

     它是 S 形的、连续的、可微的，但是它的输出值范围从-1到1（不是在 Logistic 函数的 0 到 1），这往往使每个层的输出在训练开始时或多或少都正则化了（即以 0 为中心）。这常常有助于加快收敛速度。

Relu 函数:

                                                        

     它是连续的，但不幸的是在z=0时不可微（斜率突然改变，这可以使梯度下降反弹）。然而，在实践中，它工作得很好，并且具有快速计算的优点。最重要的是，它没有最大输出值的事实也有助于减少梯度下降期间的一些问题。

这些流行的激活函数如图所示。

                       

       MLP通常用于分类，每个输出对应于不同的二进制类（例如，垃圾邮件/正常邮件，紧急/非紧急）。当类是多类的（0 到 9 的数字图像分类）时，输出层通常通过用 softmax 函数替换单独的激活函数来修改,每个神经元的输出对应于相应类的估计概率。

   Softmax回归模型首先计算出每个类别k的分数，然后对这些分数应用softmax函数，估算出每个类别的概率。注意，每个类别都有自己特定的参数向量 ，类别k的Softmax分数:   

                                                                

    计算完一个实例x每个类别的分数后，就可以通过Softmax函数来计算分数：计算出每个分数的指数，然后对它们进行归一化处理（除以所有指数的总和）:，最后取最大值。
                                              

使用交叉熵进行训练。交叉熵经常被用于衡量一组估算出的类别概率跟目标类别的匹配程度。交叉熵成本函数:               

                                                           

如果第i个实例的目标类别为k，则等于1，否则为0。当只有两个类别（K=2）时，该成本函数等价于逻辑回归的成本函数

对于类别k的交叉熵梯度向量:

                                                            

                                               

      生物神经元似乎是用 sigmoid激活函数活动的，因此研究人员在很长一段时间内坚持 sigmoid 函数。但事实证明，Relu 激活函数通常在 ANN 工作得更好。这是生物研究误导的例子之一。

二、用 TensorFlow 高级 API 训练 MLP

      DNNClassifier可以很容易训练具有任意数量隐层的深度神经网络，而 softmax 输出层输出估计的类概率。例如，下面的代码训练两个隐藏层的 DNN（一个具有 300 个神经元，另一个具有 100 个神经元）和一个具有 10 个神经元的 softMax 输出层进行分类：

import tensorflow as tf
(X_train,y_train),(X_test,y_test)=tf.keras.datasets.mnist.load_data()
X_train=X_train.astype(np.float32).reshape(-1,28*28)/255.0  #X_train：(60000, 784)

X_test=X_test.astype(np.float32).reshape(-1,28*28)/255.0
y_train=y_train.astype(np.int32)
y_test=y_test.astype(np.int32)
X_valid,X_train=X_train[:5000],X_train[5000:]
y_valid,y_train=y_train[:5000],y_train[5000:]


feature_cols=[tf.feature_column.numeric_column("X",shape=[28*28])]
dnn_clf=tf.estimator.DNNClassifier(hidden_units=[300,100],n_classes=10,feature_columns=feature_cols)
input_fn=tf.estimator.inputs.numpy_input_fn(
    x={"X":X_train},y=y_train,num_epochs=40,batch_size=50,shuffle=True)
dnn_clf.train(input_fn=input_fn)

#评估
test_input_fn = tf.estimator.inputs.numpy_input_fn(
    x={"X": X_test}, y=y_test, shuffle=False)
eval_results = dnn_clf.evaluate(input_fn=test_input_fn)


#预测
y_pred_iter = dnn_clf.predict(input_fn=test_input_fn)
#y_pred_iter生成器是一个与list非常相似的python对象。如果你迭代它（或明确使用list（pred_result））你将得到它的项目

print(y_pred_iter)#这样是不行的

y_pred = list(y_pred_iter)   #list() 方法用于将其转换为列表。
y_pred[0]

函数说明：

1、feature_columns = []，它是一个列表，通过tf.feature_column.numeric_column函数构建了Estimator中特征列，这里的fea_col 要与输入数据流中的特征数据部分一致：

numeric_column(
    key,
    shape=(1,),
    default_value=None,
    dtype=tf.float32,
    normalizer_fn=None
)

• 关键字key，特征的名字。也就是对应的列名称，避免混淆。
• 形状shape, 数据的形状，该key所对应的特征的shape. 默认是1，但是比如one-hot类型的，shape就不是1，而是实际的维度。总之，这里是key所对应的维度，不一定是1。
• 默认值default_value。
• 数据类型dtype，默认是浮点小数tf.float32。
• 标准化函数normalizer_fn，normalizer_fn:对该特征下的所有数据进行转换。如果需要进行normalize，那么就是使用normalize的函数.这里不仅仅局限于normalize，也可以是任何的转换方法，比如取对数，取指数，这仅仅是一种变换方法.

  下图是feature_col的打印输出，key为x，shape为28*28的特征列和输入数据的features的维度为28*28,保持着一致。

     

from：https://www.jianshu.com/p/fceb64c790f3

2、tf.estimator.inputs.numpy_input_fn

返回一个输入函数，根据numpy数组的dict输出特征和目标。

tf.estimator.inputs.numpy_input_fn(
    x,
    y=None,
    batch_size=128,
    num_epochs=1,
    shuffle=None,
    queue_capacity=1000,
    num_threads=1
)

x：numpy数组对象或numpy数组对象的dict。 如果是数组，则该数组将被视为单个特征。
y：numpy数组对象或numpy数组对象的dict。
batch_size：整数，要返回的批次大小。
num_epochs：整数，迭代数据的次数。 如果None将永远运行。
shuffle：Boolean，如果为True，则对队列进行洗牌。 在预测时避免随机播放。
queue_capacity：整数，要累积的队列大小。
num_threads：整数，用于读取和排队的线程数。 为了具有预测和可重复的读取和排队顺序，例如在预测和评估模式中，num_threads应为1。
from：https://tensorflow.google.cn/api_docs/python/tf/estimator/inputs/numpy_input_fn?hl=zh-cn

DNNClassifier（深度神经网络分类器）

2.1、初始化：

__init__(
    hidden_units,
    feature_columns,
    model_dir=None,
    n_classes=2,
    weight_column=None,
    label_vocabulary=None,
    optimizer='Adagrad',
    activation_fn=tf.nn.relu,
    dropout=None,
    input_layer_partitioner=None,
    config=None,
    warm_start_from=None,
    loss_reduction=losses.Reduction.SUM,
    batch_norm=False
)

参数如下：

1. hidden_units:设置隐层层数和每一层的结点数，如[64，32]代表第一隐层有64个节点，第二隐层有32个节点，所有的隐层都是全连接的。
2. feature_columns:特征列
3. model_dir:定义的是模型checkpoint保存的位置，同时也会保存将tensorboard 可视化文件，方便可视化模型的结构和loss的走向。
4. n_classes:标签的种类，默认为2
5. weight_column:由 tf.feature_column.numeric_column创建的一个字符串或者数字列用来呈现特征列。它将会被乘以example的训练损失。
6. label_vocabulary:一个字符串列表用来呈现可能的标签取值，如果给出，则必须为字符型，如果没有给出，则会默认编码为整型，为{0, 1,…, n_classes-1} 。
7. optimizer: 选择优化器，默认使用Adagrad optimizer，
8. 激活函数为tf.nn.relu。
9. input_layer_partitioner:输入层分割器，min_max_variable_partitioner和min_slice_size默认为64 << 20
10. config:一个运行配置对象，用来配置运行时间。
11. loss_reduction:定义损失函数，默认为SUM方法
12. batch_norm:是否要在每个隐层之后使用批量归一化。

2.2、方法（Methods）

2.2.1、训练train：

train(
    input_fn,
    hooks=None,
    steps=None,
    max_steps=None,
    saving_listeners=None
)

参数列表：

1. input_fn:一个用来构造用于评估的数据的函数，这个函数应该构造和返回如下的值：一个tf.data.Dataset对象或者一个包含 (features, labels)的元组，它们应当满足model_fn函数对输入数据的要求。
2. hooks:tf.train.SessionRunHook的子类实例列表，在预测调用中用于传回。
3. steps:  模型训练的次数，如果不指定，则会一直训练知道input_fn传回的数据消耗完为止。如果你不想要增量表现，就设置max_steps来替代，注意设置了steps，max_steps必须为None，设置了max_steps，steps必须为None。
4. max_steps:模型训练的总次数，注意设置了steps，max_steps必须为None，设置了max_steps，steps必须为None。
5. saving_listeners: CheckpointSaverListener对象的列表，用于在检查点保存之前或之后立即运行的回调。

2.2.2、evaluate（评估）

     评估函数，使用input_fn给出的评估数据评估训练好的模型：

evaluate(
    input_fn,
    steps=None,
    hooks=None,
    checkpoint_path=None,
    name=None
)

input_fn:一个用来构造用于评估的数据的函数，这个函数应该构造和返回如下的值：
一个tf.data.Dataset对象或者一个包含 (features, labels)的元组。
checkpoint_path:  用来保存训练好的模型
name:  如果用户需要在不同的数据集上运行多个评价，如训练集和测试集，则为要进行评估的名称，不同的评估度量被保存在单独的文件夹中，并分别出现在tensorboard中。 

评估结果：

                                                         

2.2.3、predict（预测）

predict(
   input_fn,
   predict_keys=None,
   hooks=None,
   checkpoint_path=None,
   yield_single_examples=True
)

使用训练好的模型对新实例进行预测，以下为参数列表：

1. input_fn:一个用来构造用于评估的数据的函数，这个函数应该构造和返回如下的值：一个tf.data.Dataset对象或者一个包含 (features, labels)的元组，它们应当满足model_fn函数对输入数据的要求，在后面的实例中我们会详细介绍。
2. predict_keys: 预测函数最终会返回一系列的结果，但我们可以有选择地让其输出，可供选择的keys列表为[‘logits’, ‘logistic’, ‘probabilities’, ‘class_ids’, ‘classes’]，如果不指定的话，默认返回所有值。
3. hooks:  tf.train.SessionRunHook的子类实例列表，在预测调用中用于传回。
4. checkpoint_path:  训练好的模型的目录
5. yield_single_examples:  可以选择False或是True，如果选择False，由model_fn返回整个批次，而不是将批次分解为单个元素。当model_fn返回的一些的张量的第一维度和批处理数量不相等时，这个功能是很用的。

预测的返回值是一个字典的集合，具体结果如下：

注意：predict返回的是一个与list非常相似的python对象。 使用list（pred_result），将得到它的项目

                             

• probabilities： 表示属于每个种类的可能性
• classes：表示属于哪一类（取probabilities最大的对用的类）
• class_ids：表示类的下标 ，因为实例要进行3个分类，所以是上述的结果
• logits： 一个事件发生与该事件不发生的比值的对数。假设一个事件发生的概率为 p，那么该事件的 logits 为

                                                                       

现在来看一下这个式子和 softmax 有啥关系？softmax 层会对输入进行归一化处理以得到概率分布：

                                                                        

就是softmax中的 logits， 一通就计算发现

                                                                         .

所以 tensorflow 中 logit 代表的意思并不是 logit 的数学含义。当成未归一化的概率就好。

from:https://blog.csdn.net/weixin_42499236/article/details/84189310

三、使用普通 TensorFlow 训练 DNN

3.1、构建阶段

import tensorflow as tf
#指定输入和输出的数量，并设置每个层中隐藏的神经元数量
n_inputs=28*28
n_hidden1=300
n_hidden2=100
n_outputs=10

tf.reset_default_graph()
#使用占位符节点来表示训练数据和目标
X=tf.placeholder(tf.float32,shape=(None,n_inputs),name="X")
y=tf.placeholder(tf.int32,shape=(None),name="y")

#创建一个图层
def neuron_layer(X,n_neurons,name,activation=None):
    with tf.name_scope(name):
        n_inputs=int(X.get_shape()[1])#烈数，特征数
        stddev=2/np.sqrt(n_inputs)
        init=tf.truncated_normal((n_inputs,n_neurons),stddev=stddev)
        W=tf.Variable(init,name="weights")
        b=tf.Variable(tf.zeros([n_neurons]),name="biases")
        z=tf.matmul(X,W)+b
        if activation=="relu":
            return tf.nn.relu(z)
        else:
            return z

#调用函数来创建深层神经网络        
with tf.name_scope("dnn"):
    hidden1=neuron_layer(X,n_hidden1,"hidden1",activation="relu")
    hidden2=neuron_layer(hidden1,n_hidden2,"hidden2",activation="relu")
    logits=neuron_layer(hidden2,n_outputs,"output")

#定义我们用来训练的损失函数。我们将使用交叉熵。交叉熵将惩罚估计目标类的概率较低的模型
with tf.name_scope("loss"):
    xentropy=tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,logits=logits)
    loss=tf.reduce_mean(xentropy,name="loss")
    
#定义一个GradientDescentOptimizer来调整模型参数以最小化损失函数。
learning_rate=0.01
with tf.name_scope("train"):
    optimizer=tf.train.GradientDescentOptimizer(learning_rate)
    training_op=optimizer.minimize(loss)
    
#指定如何评估模型。 我们将简单地将精度用作我们的绩效指标
with tf.name_scope("eval"):
    correct=tf.nn.in_top_k(logits,y,1)
    accuracy=tf.reduce_mean(tf.cast(correct,tf.float32))   

函数说明：

1、X是一个 2D 张量（即一个矩阵），沿着第一个维度的实例和第二个维度的特征，我们知道特征的数量将是28×28（每像素一个特征） 但是我们不知道每个训练批次将包含多少个实例。 所以X的shape是(None, n_inputs)。 y将是一个 1D 张量，每个实例有一个入口，但是我们再次不知道在这一点上训练批次的大小，所以形状(None)。

2、X.get_shape()[1]:      返回X的列数

3、tf.truncated_normal(shape, mean, stddev) :

      shape表示生成张量的维度，mean是均值，stddev是标准差。这个函数产生一个正态分布，均值和标准差自己设定。这是一个截断的产生正太分布的函数，就是说产生正态分布的值如果与均值的差值大于两倍的标准差，那就重新生成。和一般的正太分布的产生随机数据比起来，这个函数产生的随机数与均值的差距不会超过两倍的标准差，但是一般的别的函数是可能的。

     这样可以确保不会有任何大的权重，这可能会减慢训练。使用这个特定的标准差有助于算法的收敛速度更快。 重要的是为所有隐藏层随机初始化连接权重，以避免梯度下降算法无法中断的任何对称性。（如果将所有权重设置为 0，则所有神经元将输出 0，并且给定隐藏层中的所有神经元的误差梯度将相同。 然后，梯度下降步骤将在每个层中以相同的方式更新所有权重，因此它们将保持相等。 换句话说，尽管每层有数百个神经元，但是你的模型就像每层只有一个神经元一样。）

4、sparse_softmax_cross_entropy_with_logits函数

     将softmax和cross_entropy放在一起计算，即先求softmax函数，在计算交叉熵，返回值xentropy是一个M*1的张量，然后在调用reduce_mean求均值。对于分类问题而言，最后一般都是一个单层全连接神经网络，比如softmax分类器，对这个函数而言，tensorflow神经网络中是没有softmax层，而是在这个函数中进行softmax函数的计算。

    这里的logits通常是最后的全连接层的输出结果（M样本数*k类别数），labels是具体的类标签，这个函数是直接使用标签数据的，而不是采用one-hot编码形式。 lables接受直接的数字标签 如[1], [2], [3], [4] （类型只能为int32，int64） 

     此外还有一个函数softmax_cross_entropy_with_logits，其中 labels接受one-hot标签 如[1,0,0,0], [0,1,0,0],[0,0,1,0], [0,0,0,1] （类型为int32， int64）。

5、tf.nn.in_top_k(prediction, target, K):

      是用于计算预测的结果和实际结果的是否相等，返回一个bool类型的张量，prediction表示预测的结果，大小：预测样本的个数*输出的维度，每一行表示一个样本的预测概率，类型是tf.float32。target就是实际样本类别的标签，大小就是样本数量的个数。

K表示每个样本的预测结果的前K个最大的数里面是否含有target中的值。一般都是取1。（就是我们常说的top-5，top-10）

A = [[0.8,0.6,0.3], [0.1,0.6,0.4]]
B = [1, 1]
out = tf.nn.in_top_k(A, B, 1)

6、tf.cast(x, dtype, name=None)

此函数是类型转换函数，返回一个张量Tensor。输入x，dtype：转换目标类型；name：名称

7、dense()函数：

      TensorFlow 有许多方便的功能来创建标准的神经网络层，所以通常不需要像我们刚才那样定义你自己的neuron_layer()函数。 例如，TensorFlow 的fully_connected()函数和tf.layers.dense()函数，创建一个完全连接的层，其中所有输入都连接到图层中的所有神经元。 它使用正确的初始化策略来负责创建权重和偏置变量。

fully_connected()默认情况下使用 ReLU 激活函数（我们可以使用activate_fn参数来更改它）。

dense()函数与fully_connected()函数几乎相同，除了一些细微的差别：

    几个参数被重命名：scope变为name，activation_fn变为activation（同样_fn后缀从其他参数（如normalizer_fn）中删除），weights_initializer成为kernel_initializer等。默认激活函数是无，而不是tf.nn.relu。

    from tensorflow.contrib.layers import fully_connected
    with tf.name_scope("dnn"):
        hidden1 = fully_connected(X, n_hidden1, scope="hidden1")
        hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2")
        logits = fully_connected(hidden2, n_outputs, scope="outputs",
                                    activation_fn=None)

with tf.name_scope("dnn"):
    hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",
                              activation=tf.nn.relu)
    hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",
                              activation=tf.nn.relu)
    logits = tf.layers.dense(hidden2, n_outputs, name="outputs")

3.2、执行阶段

#创建一个初始化所有变量的节点，创建一个Saver来将我们训练有素的模型参数保存
init=tf.global_variables_initializer()
saver=tf.train.Saver()

def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X))#打乱顺序
    n_batches = len(X) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):##把rnd_idx分为n_batches份，不均等分割
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch

n_epochs=10;
batch_size=50
with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
            sess.run(training_op,feed_dict={X:X_batch,y:y_batch})
        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)
    save_path = saver.save(sess, "./model/my_model_final.ckpt")

with tf.Session() as sess:
    saver.restore(sess,"./my_model_final.ckpt")
    X_new_scaled=X_test[:20]
    Z=logits.eval(feed_dict={X:X_new_scaled})
    y_pred=np.argmax(Z,axis=1)

print("Predicted classes:", y_pred)
print("Actual classes:   ", y_test[:20])

3.3、Tensorboard可视化 

可视化只需在上述代码添加FileWrite方法，完整代码如下，代码修改部分用”#“标注：

################################################
from datetime import datetime
now = datetime.utcnow().strftime("%Y%m%d%H%M%S")
root_logdir = "tf_logs"
logdir = "{}/run-{}/".format(root_logdir, now)
#######################################################

import tensorflow as tf
#指定输入和输出的数量，并设置每个层中隐藏的神经元数量
n_inputs=28*28
n_hidden1=300
n_hidden2=100
n_outputs=10
tf.reset_default_graph()
#使用占位符节点来表示训练数据和目标
X=tf.placeholder(tf.float32,shape=(None,n_inputs),name="X")
y=tf.placeholder(tf.int32,shape=(None),name="y")

#创建一个图层
def neuron_layer(X,n_neurons,name,activation=None):
    with tf.name_scope(name):
        n_inputs=int(X.get_shape()[1])#烈数，特征数
        stddev=2/np.sqrt(n_inputs)
        init=tf.truncated_normal((n_inputs,n_neurons),stddev=stddev)
        W=tf.Variable(init,name="weights")
        b=tf.Variable(tf.zeros([n_neurons]),name="biases")
        z=tf.matmul(X,W)+b
        if activation=="relu":
            return tf.nn.relu(z)
        else:
            return z

#调用函数来创建深层神经网络        
with tf.name_scope("dnn"):
    hidden1=neuron_layer(X,n_hidden1,"hidden1",activation="relu")
    hidden2=neuron_layer(hidden1,n_hidden2,"hidden2",activation="relu")
    logits=neuron_layer(hidden2,n_outputs,"output")

#定义我们用来训练的损失函数。我们将使用交叉熵。交叉熵将惩罚估计目标类的概率较低的模型
with tf.name_scope("loss"):
    xentropy=tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,logits=logits)
    loss=tf.reduce_mean(xentropy,name="loss")
    
#定义一个GradientDescentOptimizer来调整模型参数以最小化损失函数。
learning_rate=0.01
with tf.name_scope("train"):
    optimizer=tf.train.GradientDescentOptimizer(learning_rate)
    training_op=optimizer.minimize(loss)
    
#指定如何评估模型。 我们将简单地将精度用作我们的绩效指标
with tf.name_scope("eval"):
    correct=tf.nn.in_top_k(logits,y,1)  #计算预测的结果和实际结果的是否相等，返回一个bool类型的张量
    accuracy=tf.reduce_mean(tf.cast(correct,tf.float32))   
#创建一个初始化所有变量的节点，创建一个Saver来将我们训练有素的模型参数保存
init=tf.global_variables_initializer()
saver=tf.train.Saver()

###################################
#放在构造期的最后，用于tensorBoard可视化
loss_summary = tf.summary.scalar('Loss', loss)
file_writer = tf.summary.FileWriter(logdir, tf.get_default_graph())
######################################

def shuffle_batch(X, y, batch_size):
    rnd_idx = np.random.permutation(len(X)) #随机排列一个数组
    n_batches = len(X) // batch_size
    for batch_idx in np.array_split(rnd_idx, n_batches):#把rnd_idx分为n_batches份，不均等分割
        X_batch, y_batch = X[batch_idx], y[batch_idx]
        yield X_batch, y_batch
n_epochs=10;
batch_size=50
with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):

            ######################################################
            summary_str = loss_summary.eval(feed_dict={X: X_batch, y: y_batch})
            file_writer.add_summary(summary_str, epoch)              
            #sess.run(training_op,feed_dict={X:X_batch,y:y_batch})
            #######################################################

        acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_val = accuracy.eval(feed_dict={X: X_valid, y: y_valid})
        print(epoch, "Batch accuracy:", acc_batch, "Val accuracy:", acc_val)
    save_path = saver.save(sess, "./model/my_model_final.ckpt")


file_writer.close()

四、微调神经网络超参数

        神经网络的灵活性也是其主要缺点之一：有很多超参数要进行调整。 不仅可以使用任何可想象的网络拓扑，而且即使在简单的 MLP 中，您可以更改层数，每层神经元数，每层使用的激活函数类型，权重初始化逻辑等等。 

      可以使用具有交叉验证的网格搜索来查找正确的超参数，但是由于要调整许多超参数，并且由于在大型数据集上训练神经网络需要很多时间， 使用随机搜索要好得多。另一个选择是使用诸如 Oscar 之类的工具，它可以实现更复杂的算法，以帮助您快速找到一组好的超参数.

4.1隐藏层数量

      一个事实：深层网络具有比浅层网络更高的参数效率：他们可以使用比浅网格更少的神经元来建模复杂的函数，使得训练更快。

      较低的隐藏层模拟低级结构（例如，各种形状和方向的线段），中间隐藏层将这些低级结构组合到模型中级结构（例如，正方形，圆形）和最高隐藏层和输出层将这些中间结构组合在一起，以模拟高级结构（如面）。

      这种分层架构还可以提高其将其推广到新数据集的能力。 例如，如果已经训练了模型以识别图片中的脸部，并且现在想要训练一个新的神经网络来识别发型，那么您可以通过重新使用第一个网络的较低层次来启动训练。 而不是随机初始化新神经网络的前几层的权重和偏置，您可以将其初始化为第一个网络的较低层的权重和偏置的值。这样，网络将不必从大多数图片中低结构中从头学习；它只需要学习更高层次的结构（例如发型）。

      对于许多问题，您可以从一个或两个隐藏层开始，它可以正常工作（例如使用只有一个隐藏层和几百个神经元，在 MNIST 数据集上容易达到 97% 以上的准确度使用两个具有相同总神经元数量的隐藏层，在大致相同的训练时间量中精确度为 98%）。对于更复杂的问题，可以逐渐增加隐藏层的数量。

4.2、每层隐藏层的神经元数量

       输入和输出层中神经元的数量由您的任务需要的输入和输出类型决定。例如，MNIST 任务需要28×28 = 784个输入神经元和 10 个输出神经元。对于隐藏的层次来说，通常的做法是将其设置为形成一个漏斗，每个层面上的神经元越来越少，原因在于许多低级别功能可以合并成更少的高级功能。但是，这种做法现在并不常见，您可以为所有隐藏层使用相同的大小 ：这样只用调整一次超参数（因为如果每层一样，比如 150，之后调就每层都调成 160）。就像层数一样，您可以尝试逐渐增加神经元的数量，直到网络开始过度拟合。一般来说，通过增加每层的神经元数量，可以增加层数，从而获得更多的消耗。

       一个更简单的方法是选择一个具有比实际需要的更多层次和神经元的模型，然后使用早期停止来防止它过度拟合（以及其他正则化技术，特别是 drop out）。

4.3、激活函数

     在大多数情况下使用 ReLU 激活函数。 与其他激活函数相比，计算速度要快一些，而梯度下降在局部最高点上并不会被卡住，因为它不会对大的输入值饱和。对于输出层，softmax 激活函数通常是分类任务的良好选择（当这些类是互斥的时）。 对于回归任务，您完全可以不使用激活函数。

from：Github官方教程