Physics-informed neural networks: A deep learning framework论文笔记
论文信息
题目:Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
期刊会议:Journal of Computational Physics
年份:18
论文地址:论文链接
代码:代码链接
基础补充
Runge-Kutta
Runge-Kutta法是用于非线性常微分方程的解的重要的一类隐式或显式迭代法
四阶Runge-Kutta法:该方法主要是在已知方程导数和初始值信息,利用计算机仿真时应用,省去求解微分方程的复杂过程
显式Runge-Kutta法:显式Runge-Kutta法是上述RK4法的一个推广。
y n + 1 = y n + h ∑ i = 1 s b i k i y_{n+1}=y_{n}+h \sum_{i=1}^{s} b_{i} k_{i} yn+1=yn+hi=1∑sbiki
其中:
k 1 = f ( t n , y n ) k 2 = f ( t n + c 2 h , y n + a 21 h k 1 ) k 3 = f ( t n + c 3 h , y n + a 31 h k 1 + a 32 h k 2 ) ⋮ k s = f ( t n + c s h , y n + a s 1 h k 1 + a s 2 h k 2 + ⋯ + a s , s − 1 h k s − 1 ) \begin{aligned} k_{1}=& f\left(t_{n}, y_{n}\right) \\ k_{2}=& f\left(t_{n}+c_{2} h, y_{n}+a_{21} h k_{1}\right) \\ k_{3}=& f\left(t_{n}+c_{3} h, y_{n}+a_{31} h k_{1}+a_{32} h k_{2}\right) \\ & \vdots \\ k_{s}=& f\left(t_{n}+c_{s} h, y_{n}+a_{s 1} h k_{1}+a_{s 2} h k_{2}+\cdots+a_{s, s-1} h k_{s-1}\right) \end{aligned} k1=k2=k3=ks=f(tn,yn)f(tn+c2h,yn+a21hk1)f(tn+c3h,yn+a31hk1+a32hk2)⋮f(tn+csh,yn+as1hk1+as2hk2+⋯+as,s−1hks−1)
0 0 0 … 0 c 2 a 21 0 … 0 ⋮ ⋮ ⋮ ⋱ ⋮ c s a s 1 a s 2 … 0 b 1 b 2 … b s = c ∣ b T \begin{aligned} &\begin{array}{c|cccc} 0&0 & 0 & \dots & 0\\ c_{2} & a_{21} & 0& \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ c_{s} & a_{s 1} & a_{s 2} & \dots & 0 \\ & b_{1} & b_{2} & \dots & b_{s} \end{array}\\ &=\frac{\mathbf{c}}{| \mathbf{b}^{\mathbf{T}}} \end{aligned} 0c2⋮cs0a21⋮as1b100⋮as2b2……⋱……00⋮0bs=∣bTc
隐式Runge-Kutta法:显式Runge-Kutta法一般来讲不适用于求解刚性方程。这是因为显式Runge-Kutta方法的稳定区域被局限在一个特定的区域里。显式Runge-Kutta方法的这种缺陷使得人们开始研究隐式Runge-Kutta方法:
y n + 1 = y n + ∑ i = 1 s b i k i y_{n+1}=y_{n}+\sum_{i=1}^{s} b_{i} k_{i} yn+1=yn+i=1∑sbiki
其中:
k i = f ( t n + c i h , y n + h ∑ j = 1 s a i j k j ) , i = 1 , … , s k_{i}=f\left(t_{n}+c_{i} h, y_{n}+h \sum_{j=1}^{s} a_{i j} k_{j}\right), \quad i=1, \ldots, s ki=f(tn+cih,yn+hj=1∑saijkj),i=1,…,s
显式Runge-Kutta方法的框架里,定义参数 a i j a i j {\displaystyle a_{ij}}a_{{ij}} aijaij的矩阵是一个下三角矩阵,而隐式Runge-Kutta方法并没有这个性质,这是两个方法最直观的区别
c 1 a 11 a 12 … a 1 s c 2 a 21 a 22 … a 2 s ⋮ ⋮ ⋮ ⋱ ⋮ c s a s 1 a s 2 … a s s b 1 b 2 … b s = c ∣ b T \begin{aligned} &\begin{array}{c|cccc} c_{1} & a_{11} & a_{12} & \dots & a_{1 s} \\ c_{2} & a_{21} & a_{22} & \dots & a_{2 s} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ c_{s} & a_{s 1} & a_{s 2} & \dots & a_{s s} \\ & b_{1} & b_{2} & \dots & b_{s} \end{array}\\ &=\frac{\mathbf{c}}{| \mathbf{b}^{\mathbf{T}}} \end{aligned} c1c2⋮csa11a21⋮as1b1a12a22⋮as2b2……⋱……a1sa2s⋮assbs=∣bTc
内容
动机
动机:
- 在分析复杂的物理,生物或工程系统的过程中,数据获取的成本过高,而且时常面临着在已知部分信息下得出结论做出决策,这些信息时常是由物理定律所描述;
- 在小数据的策略下,经过神经网络预测得到的结果缺乏鲁棒性,而且也难保证收敛;
- 考虑将这种已知的物理定律编码到学习算法中,将使得即使只有几个训练样本可用,它也可以迅速将自己引向正确的解并获得好的泛化性能。
问题定义:
非线性微分方程:
u t + N [ u ; λ ] = 0 , x ∈ Ω , t ∈ [ 0 , T ] u_{t}+\mathcal{N}[u ; \lambda]=0, x \in \Omega, t \in[0, T] ut+N[u;λ]=0,x∈Ω,t∈[0,T]
其中 u ( t , x ) u(t,x) u(t,x)隐藏解, N [ ∵ ; λ ] \mathcal{N}[\because ; \lambda] N[∵;λ]是关于 λ \lambda λ的非线性算子。
给定系统的噪声测量,主要对解决两个不同的问题感兴趣:
- Data-driven solutions of partial differential equations,第一个问题是偏微分方程的解,在给定参数 λ \lambda λ,求系统解 u ( t , x ) u(t,x) u(t,x);
- Data-driven discovery of partial differential equations第二个问题是已知系统 u ( t , x ) u(t,x) u(t,x),求 λ \lambda λ能描述观察数据。
这里论文根据输入坐标和模型参数对神经网络进行微分,从而获得具有物理信息的神经网络。得到的神经网络必须遵守观察测数据的物理定律的任何对称性,不变性或守恒原理,而观测数据是通过一般时变和非线性偏微分方程建模得到的。
Data-driven solutions of partial differential equations
连续时间模型
f : = u t + N [ u ] f:=u_{t}+\mathcal{N}[u] f:=ut+N[u]
其中,内涵物理信息的网络 f ( t , x ) f(t,x) f(t,x),尽管由于微分算子N的作用而具有不同的激活功能, f ( t , x ) f(t,x) f(t,x)与 u ( t , x ) u(t,x) u(t,x)有着相同的参数,他们之间的共享参数通过最小化均方误差来实现:
M S E = M S E u + M S E f M S E=M S E_{u}+M S E_{f} MSE=MSEu+MSEf
其中
MSE u = 1 N u ∑ i = 1 N u ∣ u ( t u i , x u i ) − u i ∣ 2 , MSE f = 1 N f ∑ i = 1 N f ∣ f ( t f i , x f i ) ∣ 2 \operatorname{MSE}_{u}=\frac{1}{N_{u}} \sum_{i=1}^{N_{u}}\left|u\left(t_{u}^{i}, x_{u}^{i}\right)-u^{i}\right|^{2},\operatorname{MSE}_{f}=\frac{1}{N_{f}} \sum_{i=1}^{N_{f}}\left|f\left(t_{f}^{i}, x_{f}^{i}\right)\right|^{2} MSEu=Nu1i=1∑Nu∣∣u(tui,xui)−ui∣∣2,MSEf=Nf1i=1∑Nf∣∣f(tfi,xfi)∣∣2
其中 { t u i , x u i , u i } i = 1 N u \left\{t_{u}^{i}, x_{u}^{i}, u^{i}\right\}_{i=1}^{N_{u}} {tui,xui,ui}i=1Nu是初边值训练点, { t f i , x f i } i = 1 N f \left\{t_{f}^{i}, x_{f}^{i}\right\}_{i=1}^{N_{f}} {tfi,xfi}i=1Nf是配置点训练数据(内部)
分析如上的损失函数
- 第一项趋于0,说明神经网络,能很好求出PDE的解,很好拟合了微分方程;
- 第二项趋于0,说明训练集上每个点都有 u N N ( x , t ) ≈ u ( x , t ) u_{N N}(x, t) \approx u(x, t) uNN(x,t)≈u(x,t)
- 这样就转化成优化损失函数
创新:
- 所有之前内嵌物理知识的机器学习算法,例如支持向量机,随机森林,高斯过程以及前馈/卷积/递归神经网络,仅作为黑盒工具。这里是通过重新修改针对基础微分算子“自定义”激活和损失函数来进一步研究。
本文通过将其导数相对于其输入坐标(即空间和时间)取导数,从而将物理信息嵌入神经网络,其中物理由偏微分方程描述。
example:
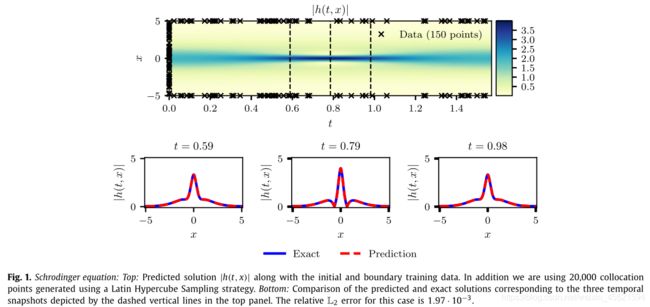
i h t + 0.5 h x x + ∣ h ∣ 2 h = 0 , x ∈ [ − 5 , 5 ] , t ∈ [ 0 , π / 2 ] h ( 0 , x ) = 2 sech ( x ) h ( t , − 5 ) = h ( t , 5 ) h x ( t , − 5 ) = h x ( t , 5 ) \begin{aligned} &i h_{t}+0.5 h_{x x}+|h|^{2} h=0, \quad x \in[-5,5], \quad t \in[0, \pi / 2]\\ &h(0, x)=2 \operatorname{sech}(x)\\ &\begin{array}{l} h(t,-5)=h(t, 5) \\ h_{x}(t,-5)=h_{x}(t, 5) \end{array} \end{aligned} iht+0.5hxx+∣h∣2h=0,x∈[−5,5],t∈[0,π/2]h(0,x)=2sech(x)h(t,−5)=h(t,5)hx(t,−5)=hx(t,5)
其中 h ( t , x ) h(t,x) h(t,x)是复值,定义 f f f
f : = i h t + 0.5 h x x + ∣ h ∣ 2 h f:=i h_{t}+0.5 h_{x x}+|h|^{2} h f:=iht+0.5hxx+∣h∣2h
定义MSE
M S E = M S E 0 + M S E b + M S E f MSE 0 = 1 N 0 ∑ i = 1 N 0 ∣ h ( 0 , x 0 i ) − h 0 i ∣ 2 MSE b = 1 N b ∑ i = 1 N b ( ∣ h i ( t b i , − 5 ) − h i ( t b i , 5 ) ∣ 2 + ∣ h x i ( t b i , − 5 ) − h x i ( t b i , 5 ) ∣ 2 ) MSE f = 1 N f ∑ i = 1 N f ∣ f ( t f i , x f i ) ∣ 2 \begin{aligned} &M S E=M S E_{0}+M S E_{b}+M S E_{f}\\ &\begin{array}{l} \operatorname{MSE}_{0}=\frac{1}{N_{0}} \sum_{i=1}^{N_{0}}\left|h\left(0, x_{0}^{i}\right)-h_{0}^{i}\right|^{2} \\ \operatorname{MSE}_{b}=\frac{1}{N_{b}} \sum_{i=1}^{N_{b}}\left(\left|h^{i}\left(t_{b}^{i},-5\right)-h^{i}\left(t_{b}^{i}, 5\right)\right|^{2}+\left|h_{x}^{i}\left(t_{b}^{i},-5\right)-h_{x}^{i}\left(t_{b}^{i}, 5\right)\right|^{2}\right) \\ \operatorname{MSE}_{f}=\frac{1}{N_{f}} \sum_{i=1}^{N_{f}}\left|f\left(t_{f}^{i}, x_{f}^{i}\right)\right|^{2} \end{array} \end{aligned} MSE=MSE0+MSEb+MSEfMSE0=N01∑i=1N0∣∣h(0,x0i)−h0i∣∣2MSEb=Nb1∑i=1Nb(∣∣hi(tbi,−5)−hi(tbi,5)∣∣2+∣∣hxi(tbi,−5)−hxi(tbi,5)∣∣2)MSEf=Nf1∑i=1Nf∣∣∣f(tfi,xfi)∣∣∣2
求解:使用五层神经网络,每层有100个神经元以及双曲正切激活函数来估计the latent function h ( t , x ) = [ u ( t , x ) , v ( t , x ) ] h(t, x)=[u(t, x) ,v(t, x)] h(t,x)=[u(t,x),v(t,x)]
离散时间模型
对 u t + N [ u ] = 0 u_{t}+\mathcal{N}[u]=0 ut+N[u]=0通过q步长的Runge–Kutta方法来表示从而得到
u n + c i = u n − Δ t ∑ j = 1 q a i j N [ u n + c j ] , i = 1 , … , q u n + 1 = u n − Δ t ∑ j = 1 q b j N [ u n + c j ] \begin{array}{l} u^{n+c_{i}}=u^{n}-\Delta t \sum_{j=1}^{q} a_{i j} \mathcal{N}\left[u^{n+c_{j}}\right], \quad i=1, \ldots, q \\ u^{n+1}=u^{n}-\Delta t \sum_{j=1}^{q} b_{j} \mathcal{N}\left[u^{n+c_{j}}\right] \end{array} un+ci=un−Δt∑j=1qaijN[un+cj],i=1,…,qun+1=un−Δt∑j=1qbjN[un+cj]
其中,满足 u n + c j ( x ) = u ( t n + c j Δ t , x ) u^{n+c_{j}}(x)=u\left(t^{n}+c_{j} \Delta t, x\right) un+cj(x)=u(tn+cjΔt,x) for j = 1 , … , q j=1, \ldots, q j=1,…,q,上式简化为
u n = u i n , i = 1 , … , q u n = u q + 1 n \begin{array}{l} u^{n}=u_{i}^{n}, i=1, \ldots, q \\ u^{n}=u_{q+1}^{n} \end{array} un=uin,i=1,…,qun=uq+1n
其中,
u i n : = u n + c i + Δ t ∑ j = 1 q a i j N [ u n + c j ] , i = 1 , … , q u q + 1 n : = u n + 1 + Δ t ∑ j = 1 q b j N [ u n + c j ] \begin{array}{l} u_{i}^{n}:=u^{n+c_{i}}+\Delta t \sum_{j=1}^{q} a_{i j} \mathcal{N}\left[u^{n+c_{j}}\right], \quad i=1, \ldots, q \\ u_{q+1}^{n}:=u^{n+1}+\Delta t \sum_{j=1}^{q} b_{j} \mathcal{N}\left[u^{n+c_{j}}\right] \end{array} uin:=un+ci+Δt∑j=1qaijN[un+cj],i=1,…,quq+1n:=un+1+Δt∑j=1qbjN[un+cj]
在这样的形式下,可以得到输入为 x x x,输出为多输出的 [ u 1 n ( x ) , … , u q n ( x ) , u q + 1 n ( x ) ] \left[u_{1}^{n}(x), \ldots, u_{q}^{n}(x), u_{q+1}^{n}(x)\right] [u1n(x),…,uqn(x),uq+1n(x)]
example
u t − 0.0001 u x x + 5 u 3 − 5 u = 0 , x ∈ [ − 1 , 1 ] , t ∈ [ 0 , 1 ] u_{t}-0.0001 u_{x x}+5 u^{3}-5 u=0, \quad x \in[-1,1], \quad t \in[0,1] ut−0.0001uxx+5u3−5u=0,x∈[−1,1],t∈[0,1]
u ( 0 , x ) = x 2 cos ( π x ) u(0, x)=x^{2} \cos (\pi x) u(0,x)=x2cos(πx)
u ( t , − 1 ) = u ( t , 1 ) u(t,-1)=u(t, 1) u(t,−1)=u(t,1)
u x ( t , − 1 ) = u x ( t , 1 ) u_{x}(t,-1)=u_{x}(t, 1) ux(t,−1)=ux(t,1)
Runge–Kutta方法得到:
N [ u n + c j ] = − 0.0001 u x x n + c j + 5 ( u n + c j ) 3 − 5 u n + c j \mathcal{N}\left[u^{n+c_{j}}\right]=-0.0001 u_{x x}^{n+c_{j}}+5\left(u^{n+c_{j}}\right)^{3}-5 u^{n+c_{j}} N[un+cj]=−0.0001uxxn+cj+5(un+cj)3−5un+cj
结果图:
- 对比了 N u , N f N_{u},N_{f} Nu,Nf取值与error关系,参与训练数据越多,得到的误差越小。(但是,训练数据相比于常见网络训练已经很少了)
- 影响离散模型算法关键参数是 q q q, Δ t \Delta t Δt
- 测试了训练样本与error关系,训练样本越多,error越小

Data-driven discovery of partial differential equations
求解逆问题:
Continuous time models
example:Navier–Stokes equation
u t + λ 1 ( u u x + v u y ) = − p x + λ 2 ( u x x + u y y ) v t + λ 1 ( u v x + v v y ) = − p y + λ 2 ( v x x + v y y ) \begin{array}{l} u_{t}+\lambda_{1}\left(u u_{x}+v u_{y}\right)=-p_{x}+\lambda_{2}\left(u_{x x}+u_{y y}\right) \\ v_{t}+\lambda_{1}\left(u v_{x}+v v_{y}\right)=-p_{y}+\lambda_{2}\left(v_{x x}+v_{y y}\right) \end{array} ut+λ1(uux+vuy)=−px+λ2(uxx+uyy)vt+λ1(uvx+vvy)=−py+λ2(vxx+vyy)
求解:参数 λ 1 \lambda1 λ1, λ 2 \lambda2 λ2
结论
引入了含物理信息神经网络,这是一类新的通用函数逼近器,它能够对含物理信息的数据集进行编码,并且可以用来描述偏微分方程。
不足
- Runge-Kutta这种融合数值方法的逼近方法,由于是通过序列迭代收敛得到解,只能求序列点上的数值,不像连续方法可以求解定义域内任意一点的值。
不懂
- 神经网络的设计,设计什么样的网络,网络深度以及训练数据大小的设计