人工智能的未来———因果推理：Causal Inference: What If chapter1 A DEFINITION OF CAUSAL EFFECT 文章解读

目录

Chapter 1

A DEFINITION OF CAUSAL EFFECT

1.1 Individual causal effects

1、a formal definition of a causal effect for an individual:

2、potential outcomes and counterfactual outcomes（潜在结果和反事实结果）

3、个人因果效应的问题

1.2 Average causal effects

1、three pieces of information to define an individual causal effect

2、three pieces of information to define an average causal effect

3、图表：条件概率

4、问题：如何判定平均因果效应存在？

5、非0平均因果效应如何表达？

6、没有平均因果效应并不意味着没有个体效应

7、Fine Point 1.1 干扰

8、 Fine Point 1.2多个版本的治疗

9、 Technical Point 1.1人群中的因果效应

1.3 Measures of causal effect

1、因果零假设

2、effect measures效果衡量指标

3、因果风险比（乘法）和因果风险差（加法）的用途

4、Fine Point 1.3需要治疗的人数NNT

1.4 Random variability

1、感兴趣人群样本

2、 采样变异性导致的随机误差

3、 随机误差的第二个来源：非确定性反事实

4、 Technical Point 1.2非确定性反事实

1.5 Causation versus association因果和关联

1、暴露和结果的独立性

2、关联度量

3、因果和关联的区别

4、问题：在哪些条件下现实世界的数据可以用于因果推理？

Chapter 1 

A DEFINITION OF CAUSAL EFFECT

本章的内容目的：

本章的目的是介绍数学符号，将你已经拥有的因果直觉形式化

确保可以将因果直觉与此处介绍的数学符号相匹配。这个符号对于精确定义

1. 1. Individual causal effects

个人因果效应：

 

1. ZEUS在接受心脏移植后五天去世，设想：如果在一月份没有接受新的心脏，五天后他还会活着----可以说明：The heart transplant intervention had a causal effect on Zeus’s five-day survival.
2. HERA一月份接受心脏移植后存活，设想：如果在一月份没有接受新的心脏，五天后他还会活着----可以说明：Hence the transplant did not have a causal effect on Hera’s five-day survival.

结论：人们推理因果关系通常通过比较采取行动A 时与不采取行动A 时的结果

注：

1、the action A as an intervention, an exposure, a policy, or a treatment.

行动A通常被称为 干预、暴露、治疗

1. Karma is another commonly used term for actions that result in out-comes.

本章符号：

A (1: treated, 0: untreated)

Y (1: death, 0: survival).

注：将诸如 A 和 Y 之类的变量称为随机变量，它们对于不同的个体可能具有不同的值

random variables（随机变量）。将个体Y所暴露的不同状况也可以称为随机变量

【技术层面上Zeus的丫不属于随机变量，因为 其结果是完全确定的专业点来说我们假设个

体的反事实结果是完全确定的】

1、a formal definition of a causal effect for an individual:

:

如果 Y a=1 ≠Y a=0，则治疗 A 对个人的结果 Y 有因果影响

①同一种治疗手段下的治疗效果不同 ②所对的是同一个个体

2、potential outcomes and counterfactual outcomes（潜在结果和反事实结果）

potential outcomes：代表暴露下可能会观察到这两种结果中的任何一种。

counterfactual outcomes：代表实际上不会发生的情况即与实事相反

注：反事实结果也可以等于他观察到的结果

For each individual, one of the counterfactual outcomes—the one that corresponds to the treatment value that the individual did receive—is actually factual. For example, because Zeus was actually treated (A = 1), his counterfactual outcome

这里的意思就是：因为真实的treatment是1，所以反事实结果中对应到treatment为1的结果就是现实中的真实结果意思就是a=0对应的反事实结果就是真实结果

consistency一致性：The equality Y = Y A is referred to as consistency

3、个人因果效应的问题

个人因果效应被定义为反事实结果值的对比，但每个个体只观察到其中一个结果，即与个体实际经历的治疗值相对应的结果。

其主要问题就是：数据缺失问题，无法完全的去对个人因果效应探究。

1. 1. Average causal effects

平均因果效应：

 

1、three pieces of information to define an individual causal effect

①比较动作a=0和 a=l

②比较反事实结果Y a = 0和Y a = 1的个体

③感兴趣的结果

2、three pieces of information to define an average causal effect

①比较的动作a = 1和a = 0

②比较结果Y a = 0和 Y a = 1的明确定义的个体群体 

• 感兴趣的结果

3、图表：条件概率

通过计算死亡人数（10）并将其除以个体总数（20）来计算治疗中的反事实风险为0.5， 这与计算人口中所有个体的反事实结果的平均值相同。

4、问题：如何判定平均因果效应存在？

答：如果感兴趣人群中的 Pr[Y a=1 = 1] ≠Pr[Y a=0 = 1]，则治疗 A 对结果 Y 的平均因果效应存在。

注：总体中的平均因果效应为空时，我们说没有平均因果效应的原假设为真。因为风险等于平均值

5、非0平均因果效应如何表达？

 该定义适用于二分结果和非二分结果

6、没有平均因果效应并不意味着没有个体效应

平均因果效应 E[Y a=1] − E[Y a=0] 总是等于单个因果效应的平均值

 E[Y a=1 − Y a=0]。Y a=1 − Y a=0，因为平均值的差值等于差值的平均值。当群体中的任何个体没有因果效应时， 即 Y a=1 = Y a=0 对于所有个体，我们说尖锐的因果零假设是正确的。尖锐的因果零假设意味着没有平均效应的零假设。

注：将“平均因果效应”简称为“因果效应”，将没有平均效应的原假设称为因果原假设

7、Fine Point 1.1 干扰

• • 对反事实结果的定义隐含地假设一个人在治疗值 a 下的反事实结果不依赖于其他人的治疗值

• • 在存在干扰的情况下，个体 i 的反事实 Y a i 没有得到很好的定义，因为个体的结果取决于其他个体的治疗值

注：个人之间的干扰在处理传染媒介或教育计划的研究中很常见，其中个人的结果受到他们与其他人口成员的社会互动的影响。

反事实结果定义的时候，自动的将其看 作一不被外界环境干扰的个体样本

1. Fine Point 1.2多个版本的治疗

①治疗值 a 下对反事实结果的定义也隐含地假设治疗值 A = a 只有一个版本

②在存在多个治疗版本的情况下，个体 i 的反事实 Y a i 没有明确定义，因为个体的结果取决于治疗 a 的版本

③Robins 和 Greenland (2000) 指出，如果特定治疗（例如心脏移植）的版本对结果（生存）具有相同的因果效应，那么反事实 Y a = 1 将是明确定义的

④不同的医生，不同的治疗手段和治疗流程

1. Technical Point 1.1人群中的因果效应
   1. 对于离散结果，平均值或期望值 E[Y a] 定义为随机变量 Y a 的所有可能值 y 的加权和
   2. 平均因果效应是最常用的群体因果效应
   3. 一般而言，群体因果效应可以定义为不同行动或治疗值下 反事实结局边际分布的任何函数的对比。

1. 1. Measures of causal effect

因果效应的度量

 

1、因果零假设

因果零假设成立，因为两个反事实风险相等时。例“：Pr[Y a=1 = 1] 和 Pr[Y a=0 = 1]都为0.5

equivalent ways of representing the causal null：等价表示方法

反事实风险表示因果空值的3种方法如下：

 

因果风险差：总体中的因果风险差是差分量表上两次因果效应 Y a=1 −Y a=0 的平均值——是平均个体因果效应的衡量标准

因果风险比：相比之下，总体中的因果风险比不是比率量表上个体因果效应Y a=1/Y a=0的平均值——它是群体因果效应的衡量标准，但不是任何个体因果效应的平均值

2、effect measures效果衡量指标

• • 这些因果参数量化了相同因果效应在不同尺度上的强度。因为因果风险差异、风险比和优势比（以及其他摘要）衡量因果关系，我们将它们称为效果衡量指标
  • 每个效果度量可用于不同的目的

3、因果风险比（乘法）和因果风险差（加法）的用途

• • 因果风险比（乘法量表）：用于计算治疗相对于不治疗，治疗增加疾病风险的次数
  • 因果风险差（加法量表）：用于计算可归因于治疗的疾病病例的绝对数量

4、Fine Point 1.3需要治疗的人数NNT

• • 对于减少平均病例数的治疗（即因果风险差异为负），NNT 等于因果风险差异绝对值的倒数
  • 

• • 对于增加平均病例数的治疗（即因果风险差异为正），可以对称地定义需要伤害的数量
  • 与因果风险差异一样，NNT 适用于它所基于的总体和时间间隔。

1. 1. Random variability

随机变异性

1、感兴趣人群样本

在实践中，调查人员只收集感兴趣人群样本的信息。即使所有研究个体的反事实结果都是已知的，使用样本也无法获得在治疗值 a 下具有结果的个体的确切比例（例如，在不治疗的情况下死亡的概率 Pr[Y a= 0 = 1] 不能直接计算。只能估计这个概率）

1. 采样变异性导致的随机误差
   • 样本比例 Pr[Y a=0 = 1] 不必完全等于超级大的群体Pr[Y a=0 = 1]。
   • 我们说 Pr[Y = 1] (HAT)是 Pr[Y a = 1] 的一致估计量，因为样本中除数的数量越大，Pr[Y = 1] 和 Pr[Y a = 1] 之间的差值就越小。发生这种情况是因为由于采样变异性引起的误差是随机的，因此遵循大数定律

    

• • 3.有关因果关系的断定

不能肯定地断定存在或不存在因果关系。相反，必须使用统计程序来评估关于因果零假设 Pr[Y a=1 = 1] = Pr[Y a=0 = 1] 的经验证据

1. 随机误差的第二个来源：非确定性反事实
   • 也许一个人的反事实结果的值不是事先固定的。随机误差的第二个来源：非确定性反事实。
   • 定义：反事实结果的值对于每个人都是固定的或确定的
   • 人们会期望这些概率因个体而异，因为并非所有个体都同样容易产生结果
   • 量子力学观点：与经典力学相反，量子力学认为结果本质上是不确定的。也就是说，如果宙斯死亡的量子力学概率为 90%，那么该理论认为，无论我们收集多少关于宙斯的数据，宙斯是否真的会发展出治疗结果的不确定性是不可减少的。

总结：随机误差的两个来源

1. Technical Point 1.2非确定性反事实

更一般地说，反事实结果的非确定性定义不会将随机变量Ya的某些特定值附加到每个个体，而是将Ya的个体特定统计分布ΘYa（·）附加到每个个体。

人群中的因果风险比：

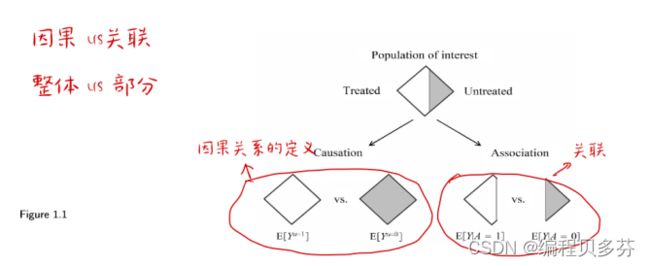
1. 1. Causation versus association因果和关联

 

1、暴露和结果的独立性

当在处理的 Pr[Y =1|A = 1] 中产生结果的个体比例等于在未处理的 Pr[Y =1|A = 0] 中产生结果的个体比例，我们说治疗 A和结果 Y 是独立的，即 A 与 Y 无关

独立性的一些等效定义

简单点来说：治疗死亡和不治疗死亡的条件概率是相同的时，即治疗A和结果Y是独立的

2、关联度量

关联风险差异、风险比和优势比（和其他度量）量化了关联存在时的强度。他们在不同的尺度上衡量关联，我们将它们称为关联度量。这些措施也受到随机变异性的影响

群里关联的定义：

对于连续结果Y，我们将治疗 和结果之间的平均独立性定义为：

3、因果和关联的区别

因果关系关注的问题：关于因果关系的推论关注的是反事实世界中的问题，例如“如果每个人都得到治疗，会有什么风险？”和“如果每个人都没有得到治疗会有什么风险？”，而关于关联的推论则与现实世界中的问题有关，例如“接受治疗的风险是什么？”和“未经治疗的风险是什么？

因果和关联的区别：关联是由个体的实际治疗值（A = 1 或 A = 0）确定的两个不相交的人群子集中的不同风险定义的，而因果关系是由同一人群中的不同风险定义的在两个不同的处理值（a = 1 或 a = 0）下

混淆概念的首次提出：在我们的人群中，存在相关性，因为治疗组 (7/13) 的死亡风险高于未治疗组 (3/7)。然而，没有因果关系，因为如果每个人都接受了治疗（10/20）的风险与每个人都没有接受治疗的风险相同。如果接受心脏移植的人平均比未接受移植的人病情更严重，那么因果关系和关联之间的差异就不足为奇了

4、问题：在哪些条件下现实世界的数据可以用于因果推理？

答：进行随机实验