机器学习之回归模型-梯度下降法求解线性回归

机器学习之回归模型-梯度下降法求解线性回归

线性回归是一种线性模型，它假设输入变量x与单个输出变量y之间存在线性关系。具体的说，就是利用线性回归模型，从一组输入变量的线性组合中，计算出输出变量y。

如果有两个或者两个以上的自变量，这样的线性回归分析，就是多元线性回归。其实，在实际生活中，一个现象往往受多个因素的影响，所以多元线性回归比一元线性回归的应用更广。

假如说：我想买西瓜，此时，我应该挑选自己满意的西瓜，那么怎么挑选呢，我们应该从从色泽，根蒂，敲打的声音等多个维度考察西瓜的质量，假如每个影响西瓜的因素和瓜的质量是线性关系，就可以写成入下线性的关系：

使用梯度下降法求解多元线性回归：
其中J为损失函数，对损失函数中的参数求偏导得到梯度，带到梯度下降公式中，使得梯度不断下降，即沿着负梯度方向，使得损失函数越来越小，即误差最小，模型越来越好。

负梯度方向：函数变化减少最快的方向，即变量沿此方向变化时，函数减少最快。

损失函数是系数的函数，如果系数沿着损失函数的负梯度变化，此时损失函数减少最快，能够以最快速度下降到最小值。

其中，梯度下降公式入下：
其中α叫做步长，也叫做学习率，这意味着我们可以通过控制及步长来控制每一步走的距离，保证不要走太快，防止错过了最低点，同时也要保证尽快收敛，故α在梯度下降中还是比较重要的，既不能太大，也不能太小。

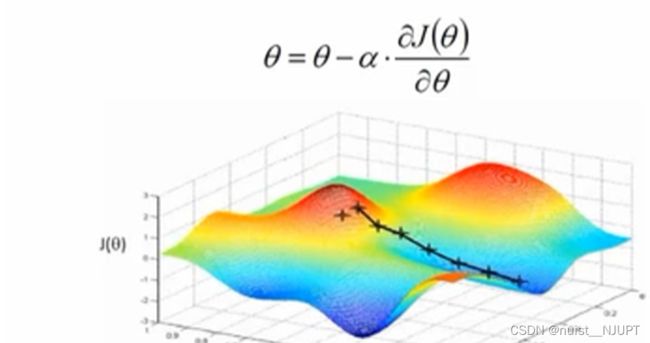
如果觉得多元线性回归的梯度下降不好理解，我们可以退回到一元线性回归的梯度下降进行观察，如下所示，其实就是不停的更新参数值，使得损失函数越来越小

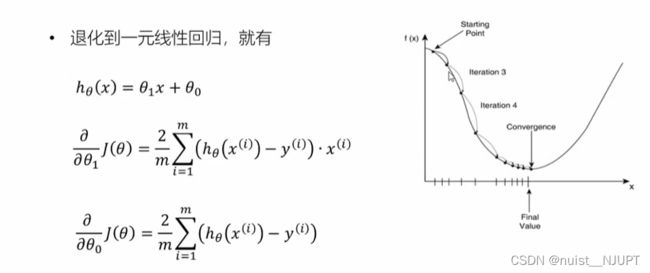
线性回归求解可以使用最小二乘法和梯度下降法，下面我们针对两种方法进行对比：
1-相同点：本质和目标相同，两种都是经典的学习算法，在给定已知数据的情况下，利用求导算出一个模型(函数)，使得损失函数最小，然后对给定的新数据进行估算预测。

2-不同点：损失函数的选择：最小二乘法必须使用平方损失函数，而梯度下降可以选取其它函数；实现方法不同，最小二乘法是实现全局最小，而梯度下降是一种迭代法；一般最小二乘法一定可以得到全局最小，但对于多元计算繁琐，且复杂情况下未必有解，而梯度下降的迭代比较简单，但找到的一般是局部最小，即极小值，仅在目标函数是下凸函数是才是全局最小，到最小点的收敛速度会变慢，且对初始点的选择极为敏感，而且步长的选择对损失函数也有影响。

使用梯度下降求解线性回归代码如下所示，
demo同步已经能上传至github，包含源代码和数据集，链接如下：https://github.com/wgdwg/-1

#梯度下降求解线性回归
import numpy as np #导入计算包
import matplotlib.pyplot as plt #导入绘图包
#1.加载数据源,并画出散点图
points = np.genfromtxt('data.csv', delimiter=',')

#提取points的两列数据，分别作为x,y
x = points[:,0] #第一列数据
y = points[:,1] #第2列数据

#用plt画出散点图
plt.scatter(x,y)
plt.show()

#2.定义损失函数,损失函数是系数的函数
def cost_function(w, b, points):
    total_const = 0 #初始化损失函数
    m = len(points) #数据个数
    #逐点计算平方误差，然后求平均数
    for i in range(m):
        x = points[i,0] #第i行，第1列
        y = points[i,1] #第i行，第2列
        total_const += (y - w * x - b) ** 2
    return total_const / m

#3.定义模型的超参数
alpha = 0.0001 #学习速率
init_w = 0 #初始参数
init_b = 0 #初始参数
num_iter = 10 #迭代次数

#4.定义核心梯度下降算法函数
def grad_desc(points, init_w, init_b, num_iter):
    w = init_w
    b = init_b
    #定义一个列表cost_list保存所有损失函数值
    cost_list = []
    for i in  range(num_iter):
        cost_list.append(cost_function(w,b,points)) #存入损失函数
        w, b = step_grad_desc(w,b,alpha,points) #不挺的更新参数w,b
    return [w, b, cost_list]

def step_grad_desc(current_w, current_b, alpha, points):
    sum_grad_b = 0
    sum_grad_w = 0
    m = len(points)
    #对每个点，带入公式求和
    for i in range(m):
        x = points[i, 0]  # 第i行，第1列
        y = points[i, 1]  # 第i行，第2列
        sum_grad_w += (current_w * x + current_b - y) * x
        sum_grad_b += (current_w * x + current_b - y) ;
    #求当前的偏导
    grad_w = 2 / m * sum_grad_w
    grad_b = 2 / m * sum_grad_b
    #梯度下降，沿负梯度方向，更新当前的w和b
    update_w = current_w - alpha * grad_w
    update_b = current_b - alpha * grad_b

    return update_w, update_b

#5.测试，运行梯度下降，计算最优的w和b
w, b, cost_list = grad_desc(points, init_w, init_b, num_iter)
cost = cost_function(w,b,points) #得到损失函数

print("参数w = ", w)
print("参数b = ", b)
print("损失函数 = ", cost)
plt.plot(cost_list)
plt.show()

#6.画出拟合曲线
plt.scatter(x,y) #原始的散点图
pred_y = (w * x) + b #预测的y
plt.plot(x,pred_y,c='r') #红色的拟合直线
plt.show() #显示绘图

梯度下降，迭代数次后，损失函数趋于最小，110左右。

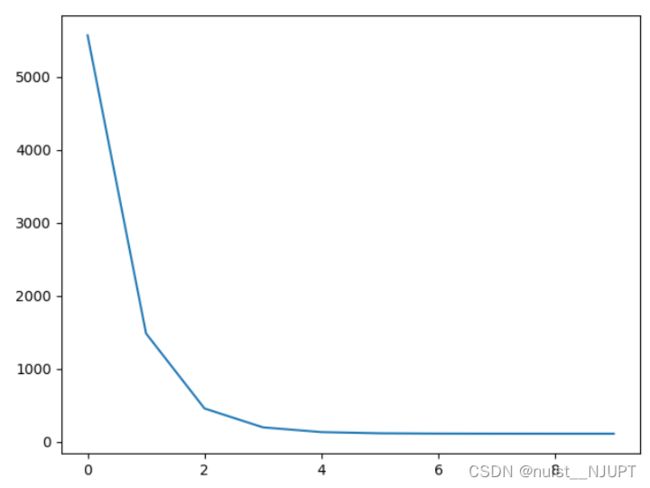
散点图的拟合直线如下所示：

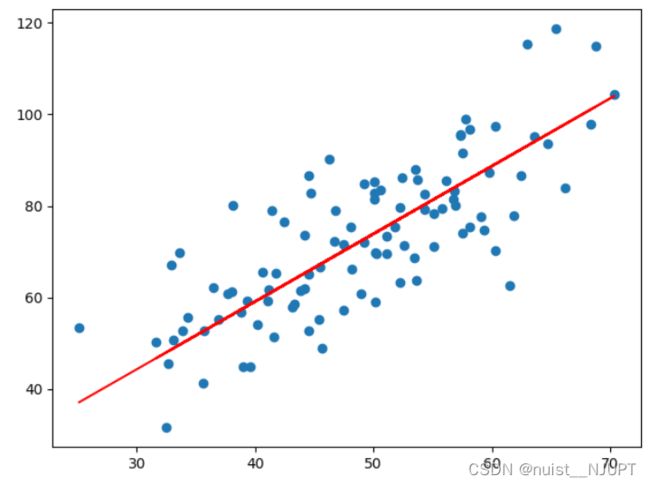
控制台输出的损失函数相对于最小二乘法稍大，即误差稍大。