机器学习 - 李宏毅笔记
李宏毅机器学习笔记
- 1.机器学习简介
-
- 1.1 机器学习项目流程
-
- 1.1.1 找到未知函数
- 1.1.2 定义训练损失函数
- 1.1.3 优化
- 2.机器学习攻略指南(实现一个好的模型)
-
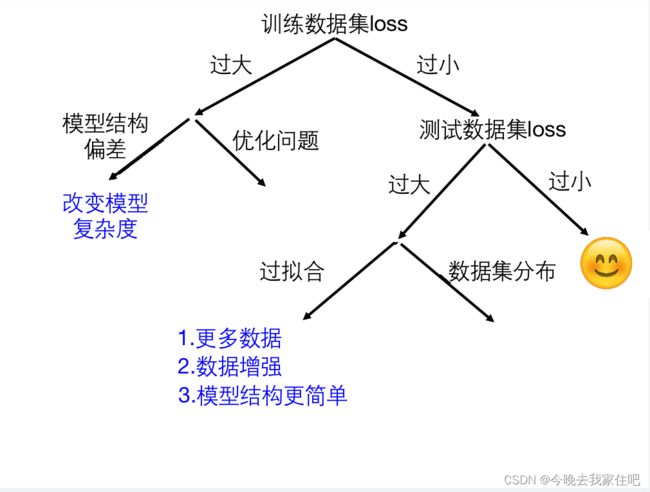
- 2.1 训练集loss过大or过小
-
- 2.1.1 如果train loss过大,如何判断是model bias还是optimize issue
- 2.1.2 model bias解决方法
- 2.1.3 Optimization issue解决方法
- 2.1.4 Optimization优化器训练技巧:Batch与Momentum
- 2.2 测试集loss过大or过小
-
- 2.2.1 如果test loss过大,如何判断是过拟合(overfit)还是是数据分布问题(mismatch)
- 2.2.2 overfit
- 2.2.3 mismatch
1.机器学习简介
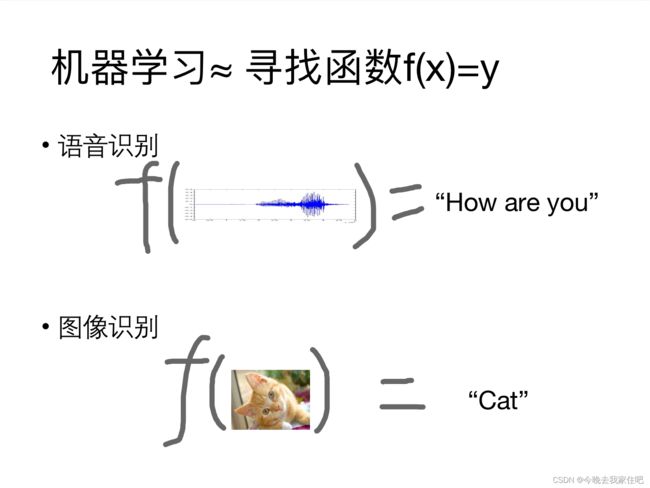
其实机器学习项目,我们可以看成是一个找函数的过程,我们向函数输入一些数据,函数返回给我们一个结果.
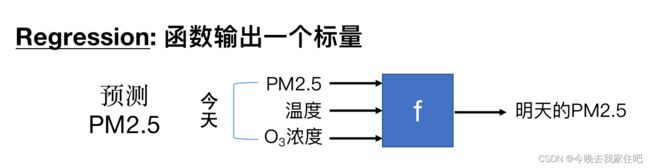
- Regression
1.1 机器学习项目流程
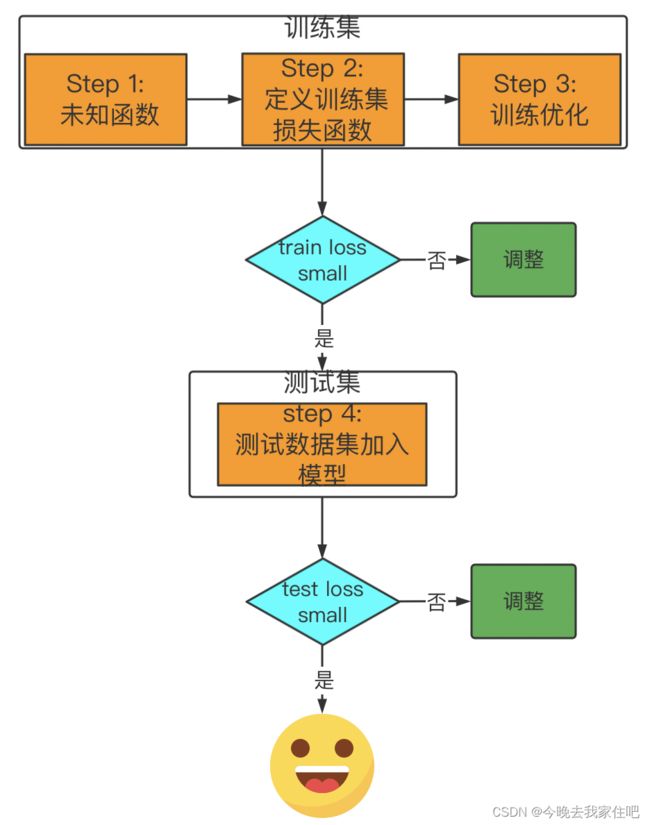
这里的调整,涉及到模型构建,定义loss很多,后面单独做分析。
从机器学习算法项目开发步骤来说,我们会先基于数据,找到构建一个稍微简单的模型,先从简单的模型入手,通过loss判断这个模型的好坏,去进行下一步模型的优化,改变。
1.1.1 找到未知函数
这里有一个函数
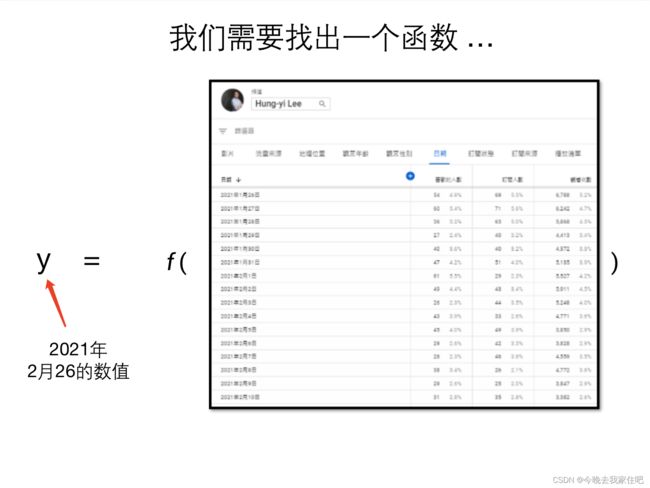
过去历史的喜欢人数数据,现在我们要通过这个数据,通过这个函数来产出(预测)未来的喜欢人数数值。
我们先简单构造一个函数
y = b + w x 1 y=b+wx_1 y=b+wx1
1.1.2 定义训练损失函数
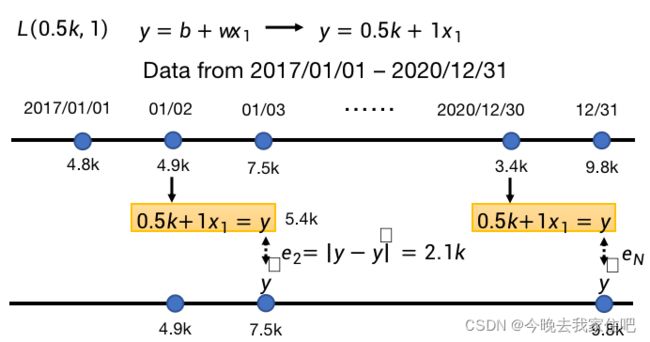
建设我们的模型参数 w w w=0.5k, b b b=1,k表示一个未知数,函数就为:
y = 0.5 k + 1 x 1 y=0.5k+1x_1 y=0.5k+1x1
现在求训练loss:
我们训练集是2017/01/01 - 2020/12/31的数据。
用这个数据集 x x x训练出的模型( f ( ) f() f()函数),再将这些数据集 x x x加入到这个函数中 f ( ) f() f(),产生的 y ^ \hat y y^与实际的 y y y,进行差值,也叫loss。
最后将每个时间点数据的loss按照不同的计算方式结合起来:

1.1.3 优化
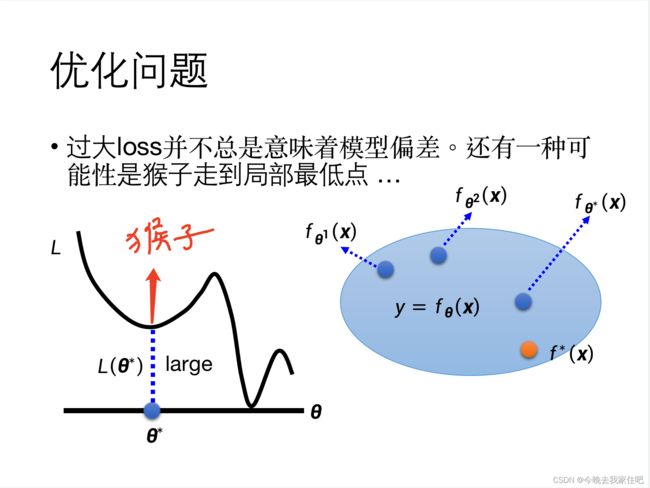
优化的目的就是让我们的 L L L(损失函数)值最小。可以看成这个猴子在找这条曲线的最低点。
简单解释一下这个公式:
w 1 ← w 0 − η ∂ L ∂ w ∣ w = w 0 w^1\leftarrow w^0-\eta\frac{\partial L}{\partial w}|_{w=w^0} w1←w0−η∂w∂L∣w=w0
其实跟我们速度公式类似:
v 1 = v 0 − a t v_1=v_0-at v1=v0−at
η \eta η就是速度的t, a a a就是 ∂ L ∂ w \frac{\partial L}{\partial w} ∂w∂L
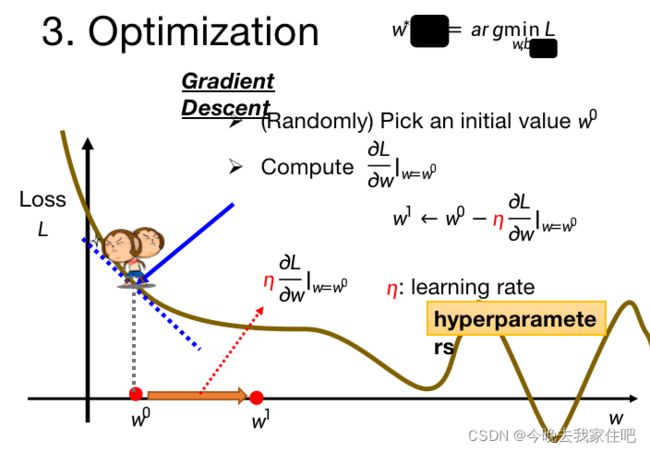
最后模型优化后的loss过小,或者过大,之后我们应该怎么样处理呢,这就是下文需要介绍的内容。
2.机器学习攻略指南(实现一个好的模型)
下次我们将讨论如何根据loss完善我们的模型,实现一个好的模型。
2.1 训练集loss过大or过小
一般是通过模型输出的物理意义、实际所需要的精度、自己期望的精度来衡量,没有具体的标准。不同的模型选择的loss函数也不同。
2.1.1 如果train loss过大,如何判断是model bias还是optimize issue
model bias(模型偏差)问题
optimize issue(优化)问题
如何判断train loss问题是model bias还是optimize issue:
这里就要用从train训练集中分离出一部分数据集为Valid验证集来判断
方法:构建一个简单的model(linear model)做看下loss,再构建一个深的model(比如神经网络)
策略:通过二个模型判断是不是mode bias,构造不同模型复杂度的模型来对比training error
1.如果当前的模型error比更复杂度的模型error对比是更小的,就说明是optimization issue
2.如果当前的模型error比更复杂度的模型error对比是更大的,就说明是model bias
2.1.2 model bias解决方法
model bias问题,很好解决,要么是降低模型复杂度,要么如下增加模型复杂度。
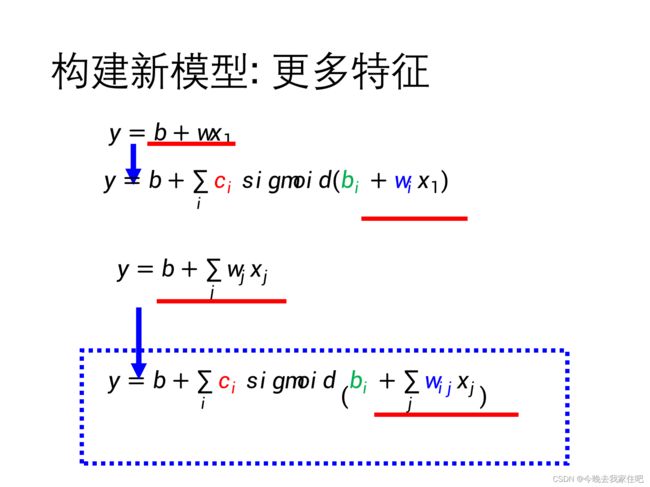
2.1.3 Optimization issue解决方法

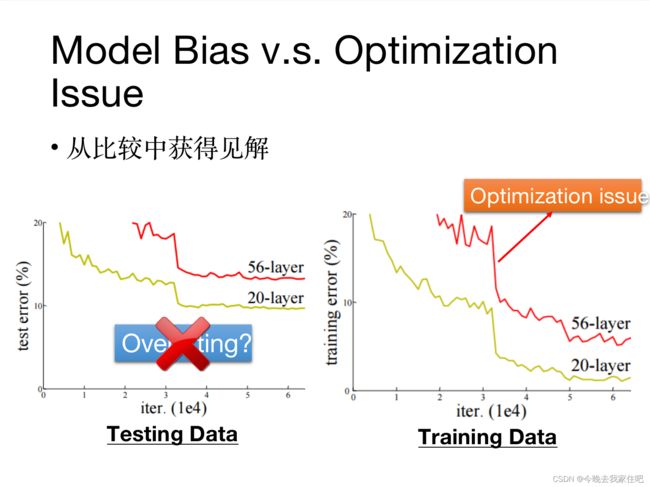
如上图所示从模型复杂度浅的模型开始,训练,对比loss
在神经网络中,理论上层越深loss越低,但是在上图中5 layer loss增大了。
这种问题就是:Optimization优化失败,简单说,就是Optimization梯度下降走到了临界点(梯度为0的critical point)。这个点一共有二种情况:
- 局部最低点(local minima)
- 鞍点(saddle point)
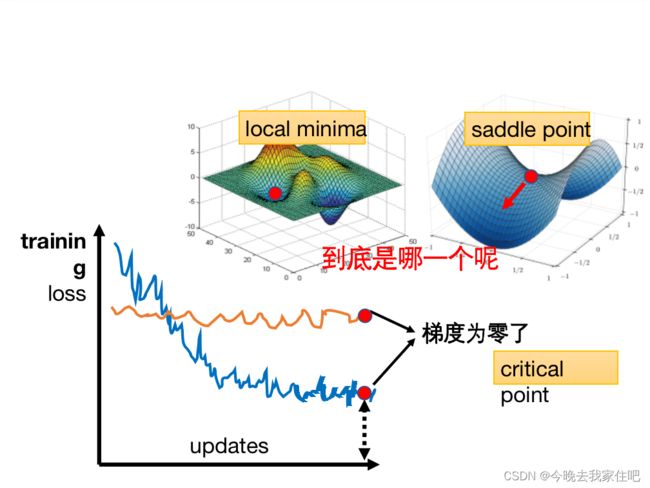
首先面临的一个问题就是,我们要判断这个梯度为零的点,是local还是saddle,这就需要我们去判断这个点附近的“地形”是什么样的,是高还是低。
我们可以看成是一个美女在山里寻找山的最低点,美女从当前的临界点(critical point)开始,往她周围的每个方向都走一点点。
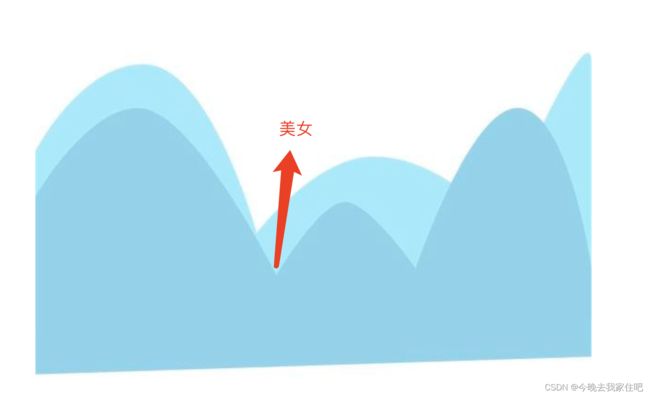

- 如果每个方向的地形高度比临界点高了,就是局部最小点(local minima)
- 如果每个方向的地形高度比临界点低了,就是局部最大点(loocal maxima)
- 如果有些方向的地形高度比临界点高,有些方向的地形高度比临界点低,就是鞍点(saddle point)
计算高度的公式如下:
L ( θ ) = L ( θ 1 ) + ( θ − θ 1 ) T g + 1 2 ( θ − θ 1 ) H ( θ − θ 1 ) L(\theta)=L(\theta^1)+(\theta-\theta^1)^Tg+\frac{1}{2}(\theta-\theta^1)H(\theta-\theta^1) L(θ)=L(θ1)+(θ−θ1)Tg+21(θ−θ1)H(θ−θ1)
学过速度位移的公式的可以把这个公式看成这个:
x 1 = x 0 + v 0 t + 1 2 a t 2 x_1=x_0+v_0t+\frac{1}{2}at^2 x1=x0+v0t+21at2
当前高度 x 0 x_0 x0加上移动后的垂直距离得到 x 1 x_1 x1

其中
g = ∂ L ( θ ) ∂ θ g=\frac{\partial L(\theta)}{\partial \theta} g=∂θ∂L(θ)可以看成速度里 ∂ x ∂ t \frac{\partial x}{\partial t} ∂t∂x,也就是 v v v速度
H = ∂ 2 ∂ 2 θ 2 L ( θ ) H=\frac{\partial^2}{\partial^2 \theta^2}L(\theta) H=∂2θ2∂2L(θ),可以看成速度里加速度求导公式:
v = d x d t v=\frac{dx}{dt} v=dtdx
a = d v d t a=\frac{dv}{dt} a=dtdv
a = d ( d x d t ) d t = d d t ∗ d x d t = d d t ∗ d d t ∗ x a=\frac{d(\frac{dx}{dt})}{dt}=\frac{d}{dt}*\frac{dx}{dt}=\frac{d}{dt}*\frac{d}{dt}*x a=dtd(dtdx)=dtd∗dtdx=dtd∗dtd∗x
g就表示当前的速度v,H就表示的加速度
由于我们求的是美女爬山的t1到t2的,这个时间间隔很小,因此可以忽略:
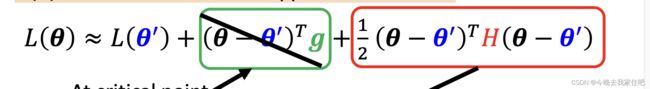
实际就只需要判断 1 2 ( θ − θ 1 ) H ( θ − θ 1 ) \frac{1}{2}(\theta-\theta^1)H(\theta-\theta^1) 21(θ−θ1)H(θ−θ1)大小就行。

2.1.4 Optimization优化器训练技巧:Batch与Momentum
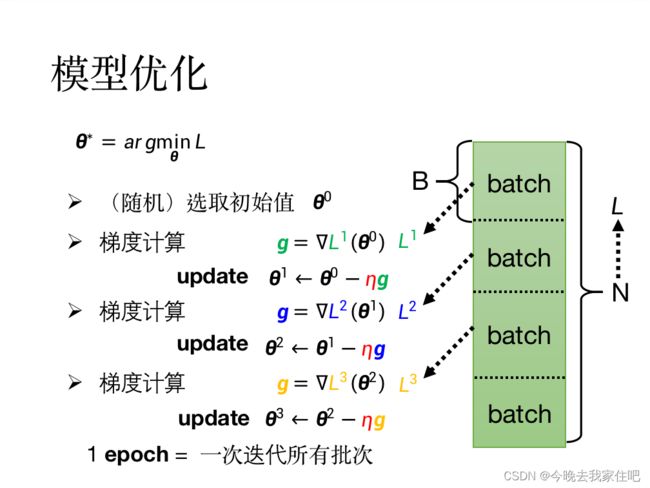
Batch
假设训练集L有N个数据,我们把数据集拆分成数量相同的几份batch,其梯度下降计算方式如下:
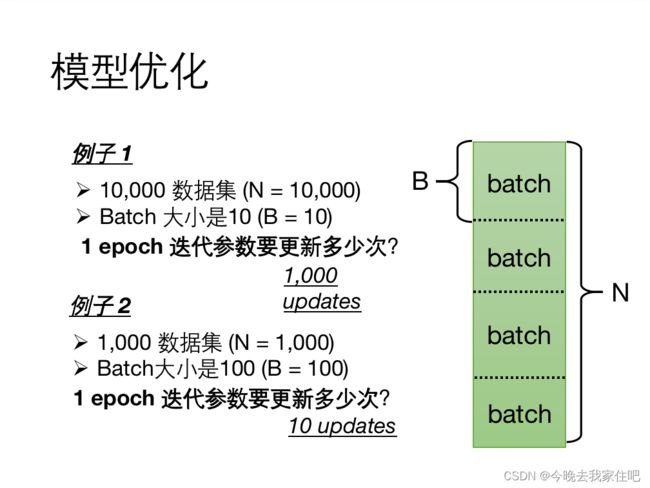
batch大小的选取对模型的计算速度和loss也是有很大影响的,如图所示:
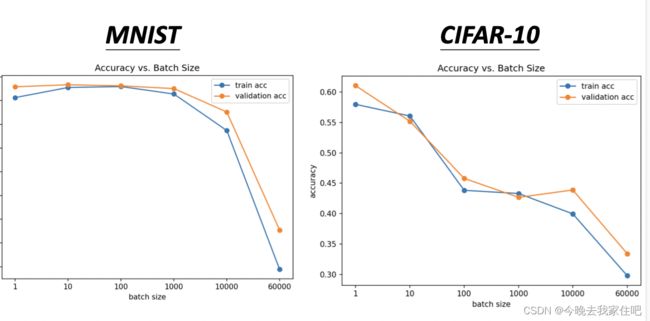
这里就直接给出一个结论了:
小的Batch v.s. 大的Batch
批量大小是一个必须确定的超参数.
| Small | Large | |
|---|---|---|
| 一次更新的速度(无并行) | 快 | 慢 |
| 一次更新的速度(并行) | 相同 | 相同 |
| 一次迭代的时间 | 慢 | 快 |
| 梯度 | 不稳定 | 稳定 |
| 优化 | 更好 | 更遭 |
| 泛化情况 | 更好 | 更糟 |
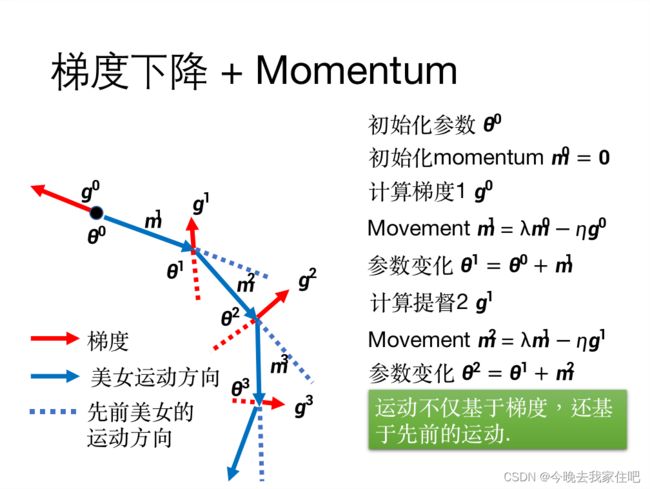
Momentum
Momentum的作用是保证美女只会在山里往下走,而不会往上走的。
这里这二张图片分别展示了没有使用Momentum与使用Momentum的效果,相信这二张图,应该大家就能看明白了
无Momentum

有Momentum
在模型训练中,数据集的划分也很重要涉及的内容:
数据集划分
2.2 测试集loss过大or过小
解决了训练集的问题,就可以把测试集的数据放入到模型中判断模型的效果了,同样的测试集loss过大过小,也是没有固定的标准的。
2.2.1 如果test loss过大,如何判断是过拟合(overfit)还是是数据分布问题(mismatch)
2.2.2 overfit
overfitting问题:
一个男的把所有精力都花在研究一个星座的女生了,最后分手了,他去认识一个其他星座的女生,就拿捏不了。

解决overfitting:
1.more training data(这种浪费时间)
2.data augmentation (自己创造数据)
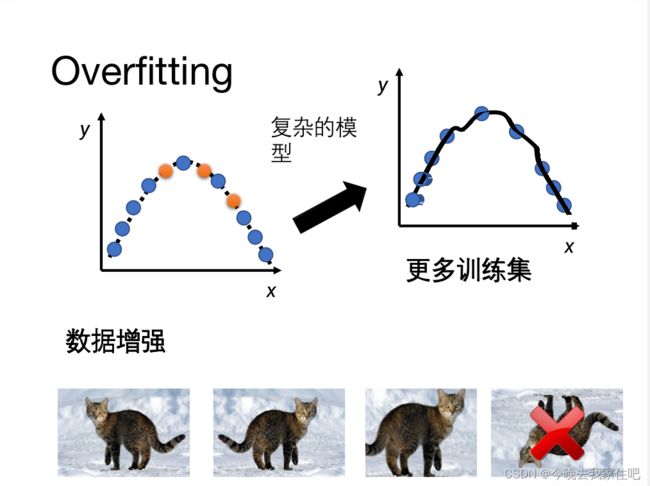
但是要注意,机器跟人也是一样的,对于有反转倒置的图片,是不太很容易识别出的。
3.constrained model(比如说线性模型告诉模型是一个一元二次方程,或者像我们的神经网络一样,unet,alexnet都是限制了模型的结构)
4.更少的参数
5.dropout
6.正则化
2.2.3 mismatch
数据分布问题。
例如说一个班级学生成绩,你训练集里只有成绩好的学生,你的测试集里只有成绩差的学生