基于麻雀搜索算法的PID神经网络解耦控制算法研究附Matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab仿真内容点击

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机

⛄ 内容介绍

耦合是指两个或两个以上的体系或两种运动形式间通过相互作用而彼此影响以至联合起来的现象。 解耦就是用数学方法将两种运动分离开来处理问题，常用解耦方法就是忽略或简化对所研究问题影响较小的一种运动，只分析主要的运动。

PID控制器(比例-积分-微分控制器)是一个在工业控制应用中常见的反馈回路部件，由比例单元P、积分单元I和微分单元D组成。PID控制的基础是比例控制;积分控制可消除稳态误差，但可能增加超调;微分控制可加快大惯性系统响应速度以及减弱超调趋势。

解耦PID控制即利用PID控制器完成解耦运算的一种方法。在多变量系统中，为了使各个被控量满足生产要求，往往需要设置若干个控制回路，而这些控制回路之间就可能相互影响、相互关连、相互耦合，其中任何一个回路的控制作用发生变化，将同时会影响其它控制回路中被控制量也发生变化。它的各个被控制量之间也互有影响，在对某一输出量进行控制时，必然使所有输出量都产生波动，其结果是使控制过程延长，震荡加剧，影响系统的稳定性。所以在设计系统时，必须注意工艺过程中各参数间相关的情况。不然若按各参数相互独立而分别设置相应的控制回路的话，轻则系统不能很好工作，影响产品质量，重则甚至发生严重生产事故。在工业过程控制中要求系统能够安全稳定地运行，有较好的调节性能，能以较小的误差跟踪设定值的变化，或使误差为零。因此需要对耦合系统进行解耦。

本文采用麻雀搜索算法优化PID解耦控制的参数，​实现最优控制。

⛄ 部分代码

function [fMin , bestX, Convergence_curve] = SSA(X, N, M, c, d, dim, fobj)

P_percent = 0.2;    % 发现者的种群规模占总种群规模的百分比

pNum = round(N*P_percent);    % 发现者数量20%

SD = pNum/2;      % 警戒者数量10%

ST = 0.8;           % 安全阈值

lb = c.*ones(1, dim);     % 下限

ub = d.*ones(1,dim);    % 上限

% 初始化

for i = 1:N

%     X(i, :) = lb + (ub - lb) .* rand(1, dim);

    fitness(i) = fobj(X(i, :));

end

pFit = fitness;

pX = X;                            % 与pFit相对应的个体最佳位置

[fMin, bestI] = min(fitness);      % fMin表示全局最优解

bestX = X(bestI, :);             % bestX表示全局最优位置

%% 迭代寻优

for t = 1 : M       

    [~, sortIndex] = sort(pFit);            % 排序

    

    [fmax, B] = max(pFit);

    worst = X(B, :);

    

    %% 发现者位置更新

    r2 = rand(1);

    if r2 < ST

        for i = 1:pNum      % Equation (3)

            r1 = rand(1);

            X(sortIndex(i), :) = pX(sortIndex(i), :)*exp(-(i)/(r1*M));

            X(sortIndex(i), :) = Bounds(X(sortIndex(i), :), lb, ub);

            fitness(sortIndex(i)) = fobj(X(sortIndex(i), :));

        end

    else

        for i = 1:pNum

            X(sortIndex(i), :) = pX(sortIndex(i), :)+randn(1)*ones(1, dim);

            X(sortIndex(i), :) = Bounds(X(sortIndex(i), :), lb, ub);

            fitness(sortIndex(i)) = fobj(X(sortIndex(i), :));

        end

    end

    

    [~, bestII] = min(fitness);

    bestXX = X(bestII, :);

    

    %% 跟随者位置更新

    for i = (pNum+1):N                     % Equation (4)

        A = floor(rand(1, dim)*2)*2-1;

        if i > N/2

            X(sortIndex(i), :) = randn(1)*exp((worst-pX(sortIndex(i), :))/(i)^2);

        else

            X(sortIndex(i), :) = bestXX+(abs((pX(sortIndex(i), :)-bestXX)))*(A'*(A*A')^(-1))*ones(1, dim);

        end

        X(sortIndex(i), :) = Bounds(X(sortIndex(i), :), lb, ub);

        fitness(sortIndex(i)) = fobj(X(sortIndex(i), :));

    end

    

    %% 警戒者位置更新

    c = randperm(numel(sortIndex));

    b = sortIndex(c(1:SD));

    for j = 1:length(b)      % Equation (5)

        if pFit(sortIndex(b(j))) > fMin

            X(sortIndex(b(j)), :) = bestX+(randn(1, dim)).*(abs((pX(sortIndex(b(j)), :) -bestX)));

        else

            X(sortIndex(b(j)), :) = pX(sortIndex(b(j)), :)+(2*rand(1)-1)*(abs(pX(sortIndex(b(j)), :)-worst))/(pFit(sortIndex(b(j)))-fmax+1e-50);

        end

        X(sortIndex(b(j)), :) = Bounds(X(sortIndex(b(j)), :), lb, ub);

        fitness(sortIndex(b(j))) = fobj(X(sortIndex(b(j)), :));

    end

    

    for i = 1:N

        % 更新个体最优

        if fitness(i) < pFit(i) 

            pFit(i) = fitness(i);

            pX(i, :) = X(i, :);

        end

        % 更新全局最优

        if pFit(i) < fMin

            fMin = pFit(i);

            bestX = pX(i, :);

        end

    end

    Convergence_curve(t) = fMin;

    

    disp(['SSA: At iteration ', num2str(t), ' ,the best fitness is ', num2str(fMin)]);

end

%% 边界处理

function s = Bounds(s, Lb, Ub)

% 下界

temp = s;

I = temp < Lb;

temp(I) = Lb(I);

% 上界

J = temp > Ub;

temp(J) = Ub(J);

% 更新

s = temp;

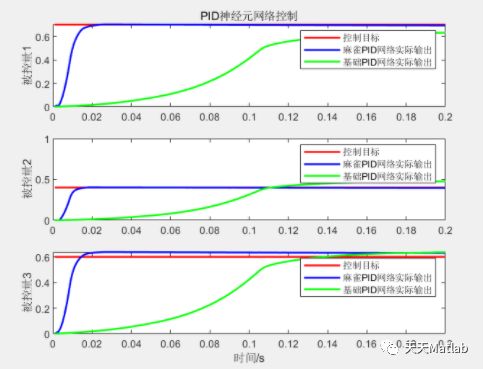
⛄ 运行结果

⛄ 参考文献

[1]王冰, 尚亚强, 严一踔,等. 基于麻雀搜索算法的橡胶复合挤出机温度压力解耦控制[J]. 大众科技, 2022, 24(7):5.

❤️ 关注我领取海量matlab电子书和数学建模资料

❤️部分理论引用网络文献，若有侵权联系博主删除