一种改进的黏菌优化算法

一、理论基础

1、黏菌算法

请参考这里。

2、改进的黏菌算法

为了克服基本SMA的缺点，本文提出了三种改进策略来提高其性能，分别是：采用基于混沌反向的学习策略增强种群多样性；采用自适应策略平衡算法的开发和探索能力；为了防止算法陷入局部最优，采用了螺旋搜索策略。下面详细介绍三种改进策略。

2.1 基于混沌反向的学习策略

基本的反向学习(Opposition-based learning, OBL)公式如下所示：$$X_i^o=lb+ub-X_i^t\text{\hspace{1em}(1)}$$其中$X_i^o$是$X_i^t$对应的反向解。
为了进一步增强种群多样性，克服基本OBL生成的反向解不一定比当前解好的不足，考虑到混沌映射具有随机性和遍历性的特点，可以帮助生成新解，增强种群多样性。因此，本文将混沌映射与OBL相结合，提出了一种基于混沌对立的学习策略。具体的数学模型描述如下：$$X_i^{To}=lb+ub-{\lambda }_i\cdot X_i^t\text{\hspace{1em}(2)}$$其中，$X_i^{To}$表示与种群中第$i$个个体对应的混沌反向解，${\lambda }_i$是对应的混沌映射值。
文献[1]的实验表明：采用Sine混沌映射的性能最好。因此，本文采取Sine混沌映射。

2.2 自适应策略

2.2.1 新的非线性递减策略

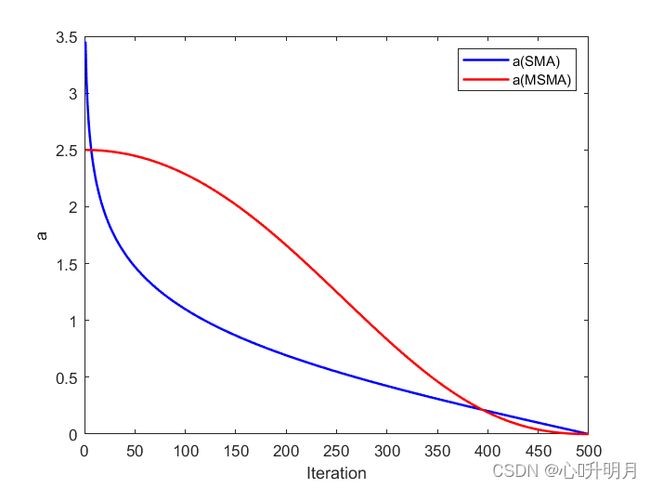
在SMA迭代优化过程中，参数$a$的变化对开发与勘探的平衡有重要影响。在SMA中，$a$在早期迭代中迅速降低，在后期迭代中减慢，早期较小的$a$不利于全局探索。因此，为了进一步平衡开发和探索，提高全局探索能力和局部开发的收敛能力，本文提出了一种新的非线性递减策略。参数$a$的新定义如下所示：$$a=2.5\cdot {\left(1-\frac{t}{t_{\max }}\right)}^{(2\cdot t/t_{\max })}\text{\hspace{1em}(3)}$$为了直观地说明新策略的效果，将其与SMA中的参数更改策略进行比较，如图1所示。本文提出的新策略在早期阶段缓慢减少，这增加了全局探索的时间。在后期迭代中，减少的速度也比原始策略快，这有利于SMA加速开发。

图1 参数a的比较

2.2.2 线性递减选择范围

原始SMA从所有群体中随机选择两个个体进行位置更新，这不利于算法的后期收敛。为了增强SMA的收敛性，个体的选择范围应该随着迭代次数的增加而减小。选择范围参数$\text{SR}$描述如下：$$\text{SR}=\text{ceil}\left(\frac{{\text{SR}}_{\min }-{\text{SR}}_{\max }}{t_{\max }}\cdot t+{\text{SR}}_{\max }\right)\text{\hspace{1em}(4)}$$其中${\text{SR}}_{\max }$和${\text{SR}}_{\min }$分别表示最大和最小选择范围。

2.3 螺旋搜索策略

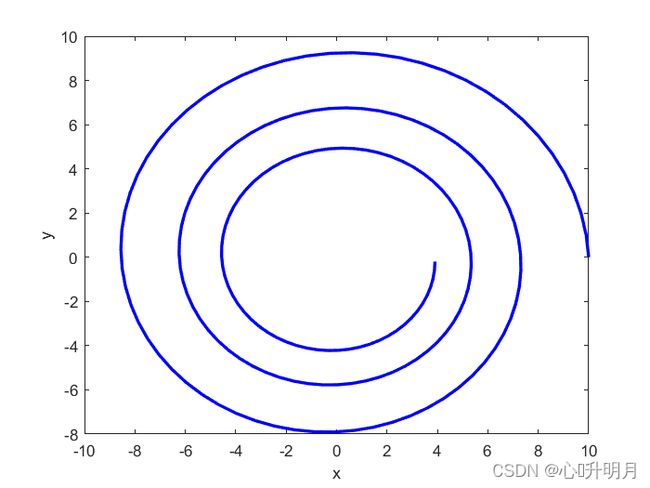
为了更好地平衡SMA的开发和探索，本文引入了螺旋搜索策略。螺旋搜索策略示意图如图2所示。
从图2可以看出，螺旋搜索策略可以扩大搜索范围，更好地提高全局探索性能。螺旋搜索策略的数学公式如下所示：$$\{\begin{array}{l}{X}_{t+1}=X_t^{\text{best}}+e^l\cdot \cos (l\cdot 2\pi )\cdot \left(X_t^{\text{best}}-X_i^t\right)\\ l=1-2\left(\frac{t}{t_{\max }}\right)\end{array}\text{\hspace{1em}(5)}$$根据更新种群位置的概率随机选择螺旋搜索策略和原始策略。因此，修改后的位置更新公式如下：$$X_{t+1}=\{\begin{array}{l}\text{rand}\cdot (ub-lb)+lb,\text{rand}<z\\ X_t^{\text{best}}+vb\cdot (W\cdot X_t^A-X_t^B),\text{rand}<p\&\text{rand}<0.85\\ X_t^{\text{best}}+e^l\cdot \cos (l\cdot 2\pi )\cdot \left(X_t^{\text{best}}-X_i^t\right),\text{rand}<p\&\text{rand}\ge 0.85\\ vc\cdot X_t,\text{rand}\ge p\&\text{rand}<0.15\\ X_t^{\text{best}}+e^l\cdot \cos (l\cdot 2\pi )\cdot \left(X_t^{\text{best}}-X_i^t\right),\text{rand}\ge p\&\text{rand}\ge 0.15\end{array}\text{\hspace{1em}(6)}$$

图2 螺旋搜索示意图

2.4 MSMA算法伪代码

提出的改进黏菌算法MSMA伪代码如图4所示。

图4 MSMA算法伪代码

二、仿真实验与结果分析

将MSMA与SMA、EO、HHO、GWO、GSA、MFO、MRFO、MPA和SSA进行对比，实验设置种群规模为30，最大迭代次数为500，每个算法独立运行30次，以文献[1]中F1、F2(单峰函数/30维)、F9、F10(多峰函数/30维)、F19、F20(固定维度多峰函数/3维、6维)为例，结果显示如下：

函数：F1
MSMA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SMA：最差值: 2.9962e-313, 最优值: 0, 平均值: 9.9873e-315, 标准差: 0, 秩和检验: 0.33371
EO：最差值: 4.833e-39, 最优值: 1.4041e-43, 平均值: 3.5862e-40, 标准差: 1.13e-39, 秩和检验: 1.2118e-12
HHO：最差值: 4.9855e-93, 最优值: 1.094e-110, 平均值: 1.6662e-94, 标准差: 9.1014e-94, 秩和检验: 1.2118e-12
GWO：最差值: 3.7727e-26, 最优值: 1.6503e-29, 平均值: 2.7418e-27, 标准差: 7.2694e-27, 秩和检验: 1.2118e-12
GSA：最差值: 7.0807e-16, 最优值: 8.0376e-17, 平均值: 2.7194e-16, 标准差: 1.5186e-16, 秩和检验: 1.2118e-12
MFO：最差值: 30000.4473, 最优值: 0.55787, 平均值: 3003.7352, 标准差: 6511.6869, 秩和检验: 1.2118e-12
MRFO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
MPA：最差值: 3.8133e-22, 最优值: 7.1971e-25, 平均值: 4.9706e-23, 标准差: 7.3317e-23, 秩和检验: 1.2118e-12
SSA：最差值: 5.045e-06, 最优值: 4.3171e-08, 平均值: 4.1574e-07, 标准差: 9.5105e-07, 秩和检验: 1.2118e-12
函数：F2
MSMA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SMA：最差值: 1.5472e-144, 最优值: 1.3668e-302, 平均值: 5.1574e-146, 标准差: 2.8248e-145, 秩和检验: 1.2118e-12
EO：最差值: 2.2361e-23, 最优值: 1.6575e-25, 平均值: 5.2337e-24, 标准差: 5.2147e-24, 秩和检验: 1.2118e-12
HHO：最差值: 8.7789e-48, 最优值: 6.9741e-59, 平均值: 2.9458e-49, 标准差: 1.6024e-48, 秩和检验: 1.2118e-12
GWO：最差值: 3.219e-16, 最优值: 1.6079e-17, 平均值: 1.1783e-16, 标准差: 9.3798e-17, 秩和检验: 1.2118e-12
GSA：最差值: 10.2201, 最优值: 5.6466e-08, 平均值: 0.77125, 标准差: 1.9745, 秩和检验: 1.2118e-12
MFO：最差值: 80.0034, 最优值: 0.19595, 平均值: 30.7785, 标准差: 20.9019, 秩和检验: 1.2118e-12
MRFO：最差值: 2.7477e-202, 最优值: 2.471e-219, 平均值: 1.7041e-203, 标准差: 0, 秩和检验: 1.2118e-12
MPA：最差值: 1.2378e-12, 最优值: 1.305e-14, 平均值: 3.2109e-13, 标准差: 3.1963e-13, 秩和检验: 1.2118e-12
SSA：最差值: 6.4248, 最优值: 0.029081, 平均值: 2.0131, 标准差: 1.807, 秩和检验: 1.2118e-12 
函数：F9
MSMA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SMA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
EO：最差值: 5.6843e-14, 最优值: 0, 平均值: 1.8948e-15, 标准差: 1.0378e-14, 秩和检验: 0.33371
HHO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO：最差值: 16.2963, 最优值: 5.6843e-14, 平均值: 2.317, 标准差: 3.842, 秩和检验: 1.0574e-12
GSA：最差值: 83.5761, 最优值: 20.8941, 平均值: 39.0355, 标准差: 13.0609, 秩和检验: 1.2118e-12
MFO：最差值: 240.2111, 最优值: 95.6545, 平均值: 163.999, 标准差: 35.8893, 秩和检验: 1.2118e-12
MRFO：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
MPA：最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SSA：最差值: 99.4956, 最优值: 33.8286, 平均值: 59.2, 标准差: 17.4863, 秩和检验: 1.2118e-12
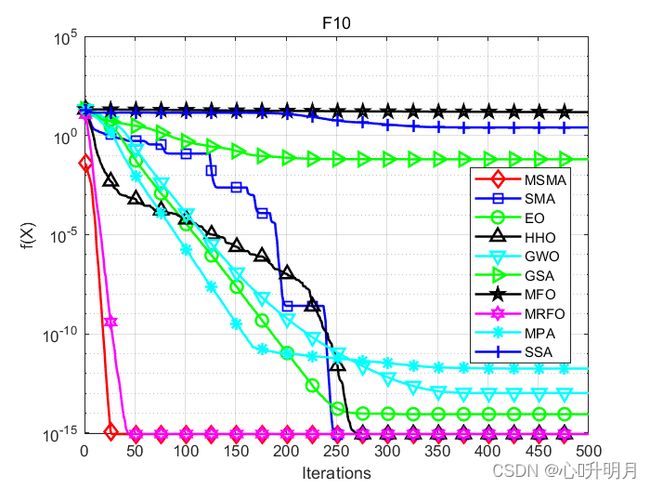
函数：F10
MSMA：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
SMA：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
EO：最差值: 1.5099e-14, 最优值: 7.9936e-15, 平均值: 8.941e-15, 标准差: 2.4567e-15, 秩和检验: 8.6442e-14
HHO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
GWO：最差值: 1.2168e-13, 最优值: 7.5495e-14, 平均值: 1.0344e-13, 标准差: 1.2817e-14, 秩和检验: 1.1257e-12
GSA：最差值: 0.96589, 最优值: 8.0735e-09, 平均值: 0.06324, 标准差: 0.24071, 秩和检验: 1.2118e-12
MFO：最差值: 19.964, 最优值: 0.24526, 平均值: 14.8856, 标准差: 6.7611, 秩和检验: 1.2118e-12
MRFO：最差值: 8.8818e-16, 最优值: 8.8818e-16, 平均值: 8.8818e-16, 标准差: 0, 秩和检验: NaN
MPA：最差值: 5.7492e-12, 最优值: 4.13e-13, 平均值: 1.7854e-12, 标准差: 1.2035e-12, 秩和检验: 1.2118e-12
SSA：最差值: 4.2114, 最优值: 8.5779e-05, 平均值: 2.5421, 标准差: 0.85413, 秩和检验: 1.2118e-12
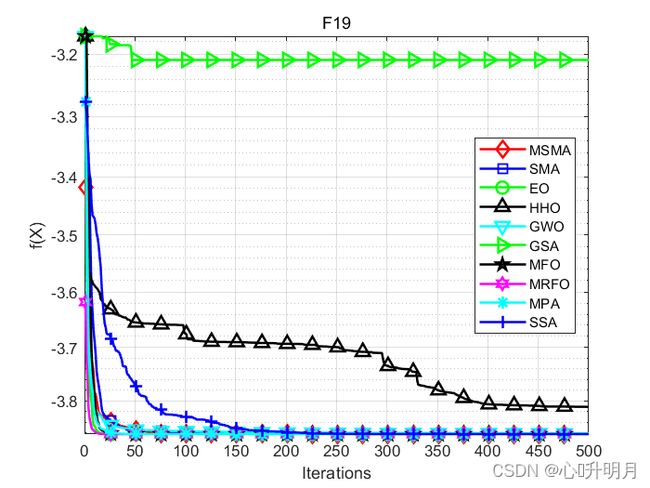
函数：F19
MSMA：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 1.5976e-12, 秩和检验: 1
SMA：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 9.362e-07, 秩和检验: 3.0199e-11
EO：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.5391e-15, 秩和检验: 1.3369e-11
HHO：最差值: -3.0898, 最优值: -3.8628, 平均值: -3.8111, 标准差: 0.19608, 秩和检验: 3.0199e-11
GWO：最差值: -3.8549, 最优值: -3.8628, 平均值: -3.8613, 标准差: 0.0026435, 秩和检验: 3.0199e-11
GSA：最差值: -2.4904, 最优值: -3.7929, 平均值: -3.2089, 标准差: 0.39533, 秩和检验: 3.0199e-11
MFO：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.7101e-15, 秩和检验: 1.2118e-12
MRFO：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.6962e-15, 秩和检验: 1.7203e-12
MPA：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 2.4491e-15, 秩和检验: 1.3369e-11
SSA：最差值: -3.8628, 最优值: -3.8628, 平均值: -3.8628, 标准差: 1.0395e-11, 秩和检验: 0.55922
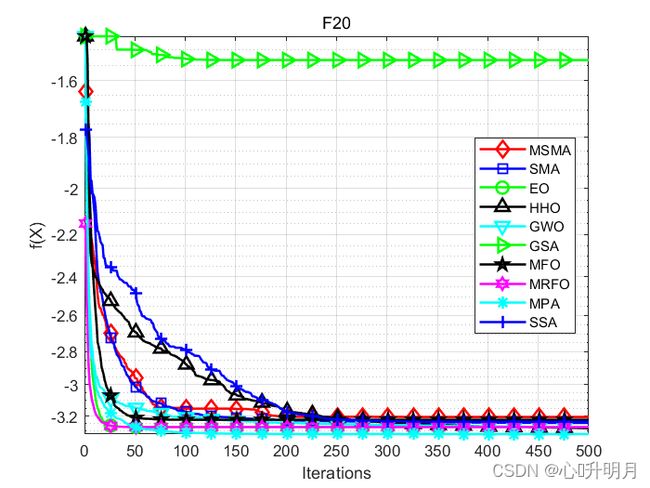
函数：F20
MSMA：最差值: -3.2031, 最优值: -3.322, 平均值: -3.2071, 标准差: 0.021707, 秩和检验: 1
SMA：最差值: -3.1981, 最优值: -3.322, 平均值: -3.2463, 标准差: 0.058535, 秩和检验: 0.053685
EO：最差值: -3.1376, 最优值: -3.322, 平均值: -3.274, 标准差: 0.065966, 秩和检验: 1.2963e-08
HHO：最差值: -3.1577, 最优值: -3.322, 平均值: -3.2829, 标准差: 0.061003, 秩和检验: 0.019112
GWO：最差值: -3.0874, 最优值: -3.322, 平均值: -3.274, 标准差: 0.079098, 秩和检验: 0.019112
GSA：最差值: -0.77782, 最优值: -2.7259, 平均值: -1.5338, 标准差: 0.49288, 秩和检验: 3.0199e-11
MFO：最差值: -2.8658, 最优值: -3.322, 平均值: -3.225, 标准差: 0.089242, 秩和检验: 2.2452e-05
MRFO：最差值: -3.2031, 最优值: -3.322, 平均值: -3.2744, 标准差: 0.059241, 秩和检验: 4.5796e-11
MPA：最差值: -3.322, 最优值: -3.322, 平均值: -3.322, 标准差: 6.8911e-12, 秩和检验: 3.0199e-11
SSA：最差值: -3.1773, 最优值: -3.322, 平均值: -3.2386, 标准差: 0.060196, 秩和检验: 0.027086

实验结果表明：MSMA具有更好的收敛精度、更快的收敛速度和更稳定的性能。

三、参考文献

[1] An-Di Tang, Shang-Qin Tang, Tong Han, et al. A Modified Slime Mould Algorithm for Global Optimization[J]. Computational Intelligence and Neuroscience, 2021, 2021: 2298215.