数据挖掘与分析课程笔记（Chapter 21）

数据挖掘与分析课程笔记

• 参考教材：Data Mining and Analysis : MOHAMMED J.ZAKI, WAGNER MEIRA JR.

文章目录

0. 数据挖掘与分析课程笔记（目录）
1. 数据挖掘与分析课程笔记（Chapter 1）
2. 数据挖掘与分析课程笔记（Chapter 2）
3. 数据挖掘与分析课程笔记（Chapter 5）
4. 数据挖掘与分析课程笔记（Chapter 7）
5. 数据挖掘与分析课程笔记（Chapter 14）
6. 数据挖掘与分析课程笔记（Chapter 15）
7. 数据挖掘与分析课程笔记（Chapter 20）
8. 数据挖掘与分析课程笔记（Chapter 21）

---

---

Chapter 21: Support Vector Machines (SVM)

21.1 支撑向量与余量

Set up：$\mathbf{D}=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^n,{\mathbf{x}}_i\in {\mathbb{R}}^d,y_i\in \{-1,1\}$，仅两类数据。

• 超平面 (hyperplanes，$d-1$ 维)：$h(\mathbf{x}):={\mathbf{w}}^T\mathbf{x}+b=w_1{x}_1+\cdots +w_d{x}_d+b$

  其中，$\mathbf{w}$ 是法向量，$-\frac{b}{w_i}$ 是 $x_i$ 轴上的截距。

• $\mathbf{D}$ 称为是线性可分的，如果存在 $h(\mathbf{x})$ 使得对所有 $y_i=1$ 的点 ${\mathbf{x}}_i$ 有 $h({\mathbf{x}}_i)>0$ ，且对所有 $y_i=-1$ 的点 ${\mathbf{x}}_i$ 有 $h({\mathbf{x}}_i)<0$ ，并将此 $h(\mathbf{x})$ 称为分离超平面。

  Remark：对于线性可分的 $\mathbf{D}$ ，分离超平面有无穷多个。

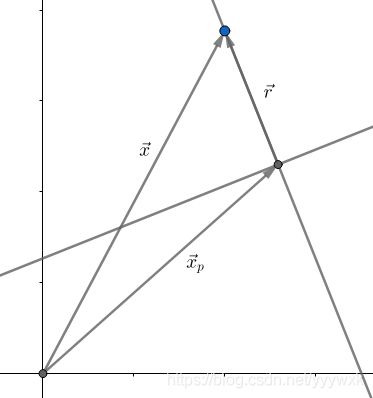
• 点到超平面的距离：
  $$\begin{gathered} \mathbf{x}={\mathbf{x}}_p+{\mathbf{x}}_r={\mathbf{x}}_p+r\cdot \frac{\mathbf{w}}{||\mathbf{w}||} \\ \begin{array}{rl}h(\mathbf{x})& =h\left({\mathbf{x}}_p+r\frac{\mathbf{w}}{\Vert \mathbf{w}\Vert }\right)\\ & ={\mathbf{w}}^T\left({\mathbf{x}}_p+r\frac{\mathbf{w}}{\Vert \mathbf{w}\Vert }\right)+b\\ & =\underset{h\left({\mathbf{x}}_p\right)}{{\mathbf{w}}^T{\mathbf{x}}_p+b}+r\frac{{\mathbf{w}}^T\mathbf{w}}{\Vert \mathbf{w}\Vert }\\ & =\underset{0}{h\left({\mathbf{x}}_p\right)}+r\Vert \mathbf{w}\Vert \\ & =r\Vert \mathbf{w}\Vert \end{array} \end{gathered}$$

  $\therefore r=\frac{h(\mathbf{x})}{\Vert \mathbf{w}\Vert },|r|=\frac{|h(\mathbf{x}|)}{\Vert \mathbf{w}\Vert }$

故 $\forall {\mathbf{x}}_i\in \mathbf{D}$ 到 $h(\mathbf{x})$ 的距离是 $y_i\frac{h({\mathbf{x}}_i)}{\Vert \mathbf{w}\Vert }$

• 给定线性可分的 $\mathbf{D}$ ，及分离超平面 $h(\mathbf{x})$ ，定义余量：
  $${\delta }^{\ast }=\underset{{\mathbf{x}}_i}{\min }\{\frac{y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)}{\Vert \mathbf{w}\Vert }\}$$
  即 $\mathbf{D}$ 中点到 $h(\mathbf{x})$ 距离的最小值，使得该 ${\delta }^{\ast }$ 取到的数据点 ${\mathbf{x}}_i$ 被称为支撑向量（可能不唯一）。

• 标准超平面：对 $\forall h(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+b$，以及任意 $s\in \mathbb{R}\setminus \{0\}$，$s({\mathbf{w}}^T\mathbf{x}+b)=0$ 与 $h(\mathbf{x})=0$ 是同一超平面。

  设 ${\mathbf{x}}^{\ast }$ 是支撑向量，若 $s{y}^{\ast }({\mathbf{w}}^T{\mathbf{x}}^{\ast }+b)=1(1)$ ，则称 $sh(\mathbf{x})=0$ 是标准超平面。

  由 $(1)$ 可得：$s=\frac{1}{y^{\ast }({\mathbf{w}}^T{\mathbf{x}}^{\ast }+b)}=\frac{1}{y^{\ast }h({\mathbf{x}}^{\ast })}$

  此时，对于 $sh(\mathbf{x})=0$ ，余量 ${\delta }^{\ast }=\frac{y^{\ast }h({\mathbf{x}}^{\ast })}{\Vert \mathbf{w}\Vert }=\frac{1}{\Vert \mathbf{w}\Vert }$

事实：如果 ${\mathbf{w}}^T\mathbf{x}+b=0$ 是标准超平面，对 $\forall {\mathbf{x}}_i$ ，一定有 $y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1$

21.2 SVM: 线性可分情形

目标：寻找标准分离超平面使得其余量最大，即 $h^{\ast }=\arg \underset{\mathbf{w},b}{\max }\{\frac{1}{\mathbf{w}}\}$

转为优化问题：
$$\begin{array}{rl}& \underset{\mathbf{w},b}{\min }\{\frac{\Vert \mathbf{w}{\Vert }^2}{2}\}\\ & \text{s.t.}{y}_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,\forall ({\mathbf{x}}_i,y_i)\in \mathbf{D}\end{array}$$
引入 Lagrange 乘子 ${\alpha }_i\ge 0$ 与 KKT 条件：
$${\alpha }_i(y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)-1)=0$$
定义：
$$L(\mathbf{w})=\frac{1}{2}\Vert \mathbf{w}{\Vert }^2-\sum _{i=1}^n{\alpha }_i(y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)-1)(2)$$

$$\begin{array}{l}\frac{\partial }{\partial \mathbf{w}}L=\mathbf{w}-\sum _{i=1}^n{\alpha }_i{y}_i{\mathbf{x}}_i=0(3)\\ \frac{\partial }{\partial b}L=\sum _{i=1}^n{\alpha }_i{y}_i=0(4)\end{array}$$

将 (3)(4) 代入 (2) 得：
$$\begin{array}{rl}{L}_{dual}& =\frac{1}{2}{\mathbf{w}}^T\mathbf{w}-{\mathbf{w}}^T(\underset{\mathbf{w}}{\sum _{i=1}^n{\alpha }_i{y}_i{\mathbf{x}}_i})-b\underset{0}{\sum _{i=1}^n{\alpha }_i{y}_i}+\sum _{i=1}^n{\alpha }_i\\ & =-\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{i=1}^n{\alpha }_i\\ & =\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\end{array}$$
故对偶问题为：
$$\begin{array}{rl}& \underset{\alpha }{\max }{L}_{dual}=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\\ & \text{s.t.}\sum _{i=1}^n{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,\forall i\end{array}$$
利用二次规划解出 Dual：${\alpha }_1,\cdots ,{\alpha }_n$

代入 (3) 可得：$\mathbf{w}=\sum _{i=1}^n{\alpha }_i{y}_i{\mathbf{x}}_i$

使得 ${\alpha }_i>0$ 的数据 ${\mathbf{x}}_i$ 给出支撑向量。

对于每一个支撑向量：$y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)-1\Rightarrow b=\frac{1}{y_i}-{\mathbf{w}}^T{\mathbf{x}}_i$

取 $b={\mathrm{avg}}_{{\alpha }_i>0}\{b_i\}$

---