基于寄生-捕食算法的函数寻优算法

一、理论基础

1、寄生-捕食算法

文献[1]提出了一种新的元启发式优化方法—寄生-捕食算法(Parasitism-Predation Algorithm, PPA)，该算法在乌鸦-布谷鸟-猫系统模型中模拟捕食者(猫)、寄生虫(布谷鸟)和宿主(乌鸦)之间的相互作用，以克服大数据的低收敛性和维数诅咒的问题。

（1）初始化

通过获得$n$个最佳鸟巢，评估所有新的解决方案以解决$d$维优化问题，如下所示：$$X_i^{new}=X_i^{\min }+r_1(X_i^{\max }-X_i^{\min })\text{\hspace{1em}(1)}$$其中，$X_i^{new}$是初始解($i=1,2,\dots ,n$)，$X_i^{\min }$是下限，$X_i^{\max }$是上限，$r_1$是从0到1之间的均匀分布中提取的随机变量。

（2）筑巢阶段(鸟窝)

初始化后，优化算法将进入筑巢阶段、寄生阶段和捕食阶段。一开始，随着时间的推移，猫减少了乌鸦的数量。通过模拟乌鸦飞行的两种状态来评估筑巢阶段。第一种状态是通过生成随机候选乌鸦，为乌鸦$i$生成一个新位置，如下所示：$$X_i^{t+1}=X_i^t+F(X_{r_1}-X_i^t)\forall i\in n_{crow}\text{\hspace{1em}(2)}$$其中，$r_1$是一个随机指数，$F$是一个Levy飞行步长，它是基于$\propto$稳定分布计算的，具有使用不同步长跨越大尺度距离的能力。$Levy(\sigma ,\mu )$分布的简单版本密度是：$$f(q)=\sqrt{\frac{\gamma }{2\pi }}\frac{1}{(q-\mu {)}^{3/2}}\exp \left(-\frac{\sigma }{2(q-\mu )}\right)0<\mu <q<\infty \text{\hspace{1em}(3)}$$使用蒙特卡洛算法生成具有与Levy飞行相同行为的随机样本$L_i$，用于模拟$\propto$稳定分布：$$L_i\sim step\oplus Levy(\propto )\sim 0.01\frac{u}{|y{|}^{1/\alpha }}\text{\hspace{1em}(4)}$$其中，$step$是与问题规模相关的缩放系数，$u=N(0,{\sigma }_u^2)$和$y=N(0,{\sigma }_y^2)$分别是满足${\sigma }_u={\left[\frac{\Gamma (1+\alpha )\sin (\pi \alpha /2)}{\Gamma ((1+\alpha )/2)\alpha 2^{(\alpha -1)/2}}\right]}^{1/\alpha },{\sigma }_y=1$的正态分布，$\oplus$表示矢量乘法。
在筑巢阶段，通过Levy飞行过程，利用当前最佳巢群更新解，发现鸟窝。Levy飞行已经在许多物种中被观察到，这是一种随机游走。Levy飞行的步长由重尾概率分布控制，通常称为Levy分布。Levy飞行在搜索空间的探索上优于均匀随机分布，因此用它代替均匀随机运动来模拟陷入局部最优、过早收敛的规避行为，提高整体搜索空间的探索能力。第二步是通过重新初始化被违反的维度，从之前的状态修改被违反的维度，如下所示：$$X_{i,out}^{new}=X_{i,out}^{\min }+\left(X_{i,out}^{\max }-X_{i,out}^{\min }\right)rand[0,1]\forall out\in violateddimension\text{\hspace{1em}(5)}$$重新初始化“呈现总体的随机变化，以获得增强的探索和增强搜索空间的多样性。这一阶段被设计为纯粹的探索阶段，在第一种状态下使用Levy飞行，提供在整个搜索空间中散布乌鸦的高能力。此外，超出边界外的维度都要受到约束。

（3）寄生阶段(乌鸦-布谷鸟)

一开始，当捕食效率较低时，猫会将布谷鸟赶尽杀绝；捕食效率高时，导致布谷鸟灭绝。布谷鸟的效率被假定为弱/中等，而猫的效率则降低了。在此阶段，将部分乌鸦卵(宿主)替换为布谷鸟卵，布谷鸟卵与乌鸦卵相似，被发现的可能性较小。此外，根据适应度值选择被寄生的巢，巢越好，被寄生的几率越大。构建新的巢穴来取代一些巢穴，并以概率$p_a$发现一小部分较差的巢穴。布谷鸟的新巢可以通过下式得到：$$X_{i,new}^{cuckoo}=X_{i,old}^{cuckoo}+S_G\cdot k\text{\hspace{1em}(6)}$$$$S_G=(X_{r_2}-X_{r_3})rand[0,1]\text{\hspace{1em}(7)}$$其中，$X_{i,old}^{cuckoo}$是通过轮盘赌选择的个体；$S_G$是均匀高斯分布步长；$k$定义为二进制矩阵，计算如下：$$k=rand[0,1]>p_a\text{\hspace{1em}(8)}$$其中，$p_a$是由$t/2T$或$g/2G$给出的递增因子，其中$T$或$G$是最大迭代次数，$t$或$g$是当前迭代次数。采用二元矩阵$k$尽可能保留老布谷鸟的相当部分，保留探索搜索空间。寄生阶段开始时，矩阵$k$被1填充。然后，增加其价值以改善种群。
由于布谷鸟分泌的驱虫剂，寄生鸟巢被捕食的可能性要小得多。在鸟巢内，有布谷鸟雏鸟的鸟会有更少的乌鸦。根据捕食的压力有多大，这种过程产生的平衡影响范围基本上是从寄生到筑巢。

（4）捕食阶段(乌鸦-猫)

一开始，强大的捕食效率导致猫和乌鸦的爆炸性增长减少，无法为布谷鸟提供足够的生存资源，因此布谷鸟灭绝。这个阶段基于猫的追踪模式，可以是乌鸦-猫阶段。不需要执行搜索模式，因为猫知道空的搜索空间并且不需要搜索。在这个阶段，布谷鸟雏鸟会释放出排斥猫的排斥性化合物。猫追踪巢穴时，臭味分泌物很少，而不是被布谷鸟占据，并随机选择非寄生巢穴作为追踪模式。一旦猫开始追踪猎物，它们就会根据自己的速度在各个维度上移动。猫的强捕食效率导致猫的爆炸性增长，乌鸦和杜鹃的低增长。该阶段包括三个步骤：
步骤1：更新各个维度的速度如下：$$v_{k,d}=v_{k,d}+r.c.(x_{best,d}-x_{k,d}),d=1,2,\cdots ,M\text{\hspace{1em}(9)}$$其中，$v_{k,d}$表示$ca{t}_k$第$d$维上的速度，$x_{best,d}$是具有最佳适应值的猫的位置，$x_{k,d}$是$ca{t}_k$的位置，$c$是常数，$r$是$[0,1]$范围内的随机值。
步骤2：检查更新速度是否超过最大速度范围。在新速度大于最大速度的情况下，它被设置为等于极限(速度极限被修改为从1线性下降到0.25)
步骤3：更新$ca{t}_k$的位置如下：$$x_{k,d}=x_{k,d}+v_{k,d}\text{\hspace{1em}(10)}$$

2、PPA算法伪代码

PPA算法的伪代码如图1所示。

图1 PPA算法伪代码

二、仿真实验与结果分析

对PPA算法单独实验，以常用23个测试函数中的F3、F4(单峰函数/30维)、F9、F10(多峰函数/30维)、F20、F21(固定维度多峰函数/6维、4维)为例，实验设置种群规模为30，最大迭代次数为1000，每种算法独立运算30次，结果显示如下：

函数：F3
PPA：best: 128.2791, worst: 2096.902, mean: 564.3674, std: 369.7015
函数：F4
PPA：best: 25.5105, worst: 51.9664, mean: 37.5791, std: 6.8245
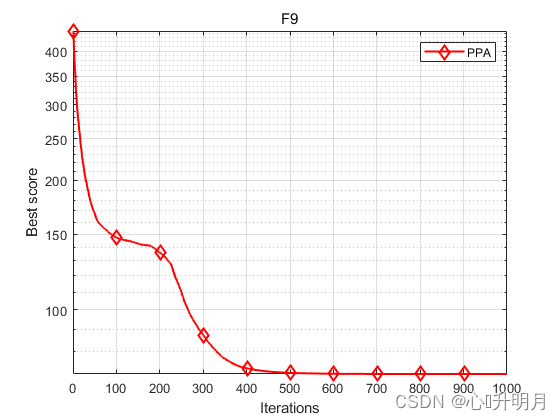
函数：F9
PPA：best: 36.8724, worst: 121.3954, mean: 70.894, std: 22.0422
函数：F10
PPA：best: 9.6145, worst: 16.0049, mean: 12.8844, std: 1.6332
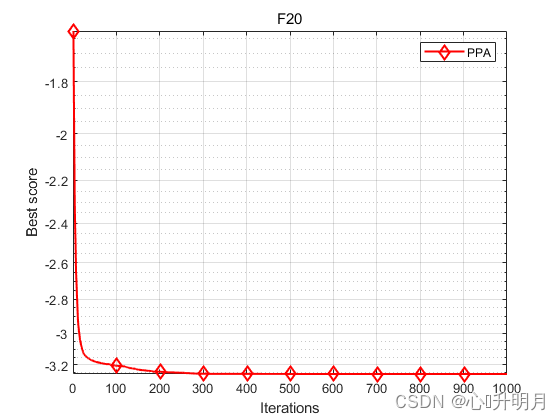
函数：F20
PPA：best: -3.322, worst: -3.1164, mean: -3.2602, std: 0.074985
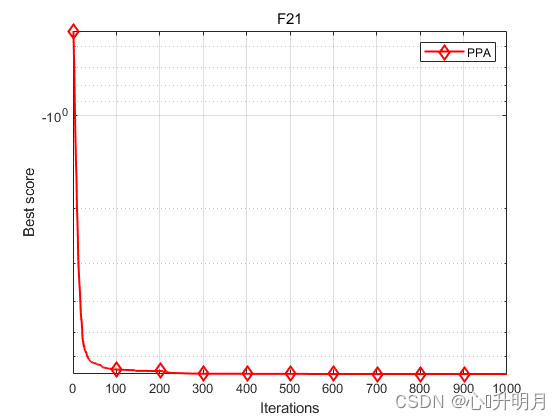
函数：F21
PPA：best: -10.1532, worst: -2.2426, mean: -6.8288, std: 3.0824

实验结果表明：PPA算法在求解优化问题上具有良好的性能。

三、参考文献

[1] Al-Attar A. Mohamed, S.A. Hassan, A.M. Hemeida, et al. Parasitism – Predation algorithm (PPA): A novel approach for feature selection[J]. Ain Shams Engineering Journal, 2020, 11: 293-308.