【计算机视觉与深度学习北邮鲁鹏】自学笔记
目录
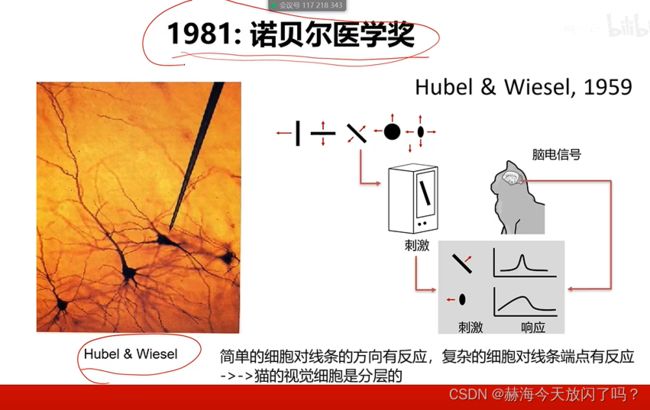
- 第1章 前言
- 第2章 图像分类
-
- 1. 什么是图像分类任务?
- 2. 图像分类任务的难点?
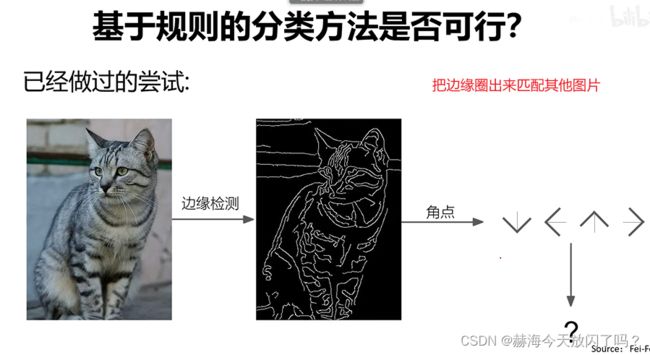
- 3. 基于规则的方法是否可行?
- 4. 什么是数据驱动的图像分类范式?
-
- 1)图像表示
-
- a)像素表示
- b)全局特征表示
- c)局部特征表示
- 2)分类器
- 3)损失函数
- 4)优化算法
- 5. 常用的评价指标
- 第3章 线性分类器
-
- 1. 基本介绍
-
- 1)数据集
- 2)图像类型
- 3)图像表示
- 5)什么是线性分类器
- 6)举例说明
- 2. 细节理解
-
- 1)权值向量
- 2)如何衡量分类器对当前样本的效果好坏?
- 3)多类支撑向量机损失
- 3. 损失函数
-
- 1)什么是损失函数?
- 2)正则项与超参数
- 4. 优化
-
- 1)什么是参数优化?
- 2)梯度下降算法
- 5. 训练过程
-
- 1)数据集划分
- 2)交叉验证
- 第4章 全连接神经网络
-
- 1. 多层感知器
- 2. 激活函数
- 3. 损失函数
-
- 1)softmax
- 2)交叉熵损失
- 3)对比多类支撑向量机损失
- 4. 优化算法
-
- 1)计算图和反向传播
- 2)再谈激活函数
- 5. 梯度算法改进
-
- 1)动量法
- 2)自适应梯度与RMSProp
- 6. 权值初始化
-
- 1)全零初始化(×)
- 2)随机初始化
- 7. 批归一化
- 8. 过拟合
- 第5章 卷积
第1章 前言
第2章 图像分类
1. 什么是图像分类任务?

图像搜索是我根据给出的图片在网上找到一模一样的图片;图像识别是我根据给出的图片识别出来它是什么。
2. 图像分类任务的难点?
换个角度可能就不能很好地识别出来是同一个人。

算法能否应对光线多变的情况?

计算机系统应该要能自适应远近

系统提取到的特征在图片中只有很小一部分,特征不显著的时候还能识别成功吗?(抗遮挡认知)

特征不一定是很死板的那些,会变的话你也能识别吗?

跟背景相似性大时难以识别?
![]()



遇到图像分类的任务,先按照以上提出难点去设计,针对每个难点有对应的处理方法,主要是要拆解出自己的任务对应到了哪些难点。
3. 基于规则的方法是否可行?
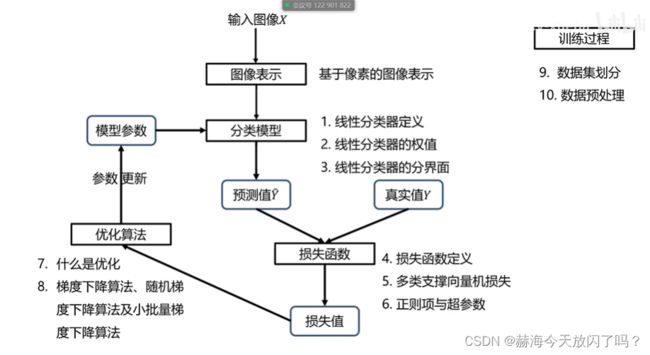
4. 什么是数据驱动的图像分类范式?
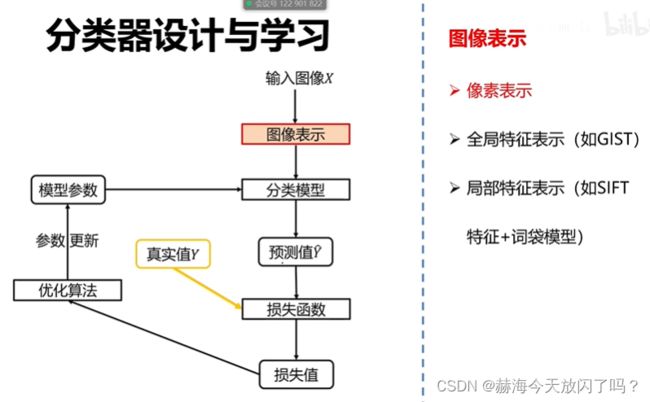
1)图像表示
a)像素表示
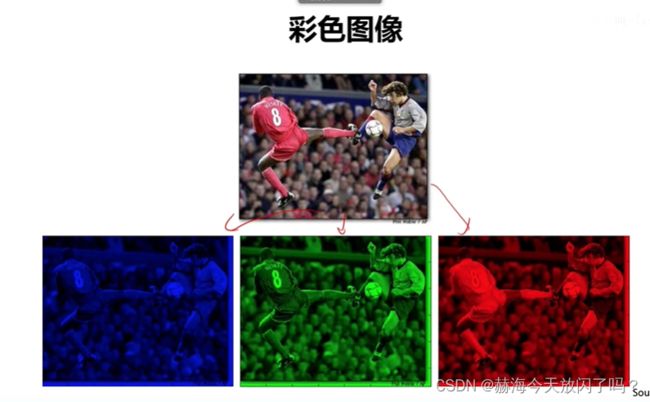
比如RGB是三通道,每个点有3个通道,如果有1个图是300300大小的话,那它就是300300深度是3的一个矩阵。(我们把计算机中存储单个像素点所用的 bit 位称为图像的深度)
关于图像三通道和单通道的解释
图像的通道和深度以及图像的像素点操作完全解析
b)全局特征表示
适合于全景图,风景啊,街景啊之类的。对于要考虑细节的、遮挡的就不太合适。
c)局部特征表示
比如从图像中抽取出100个有典型意义的区块,用这些区块来表示这个图。这样的话对遮挡问题也能解决,如果一只眼睛被遮挡住了,还有另外一只,还是可以匹配成功。但是如果你用全局特征表示的话,本来是有两只眼睛的,你遮挡了一只很有可能就匹配失败。
图像识别其实就两件事,第一是将图像表示成有意义的特征,二是用特征去识别。如果特征表示地越好就越容易被识别出来。
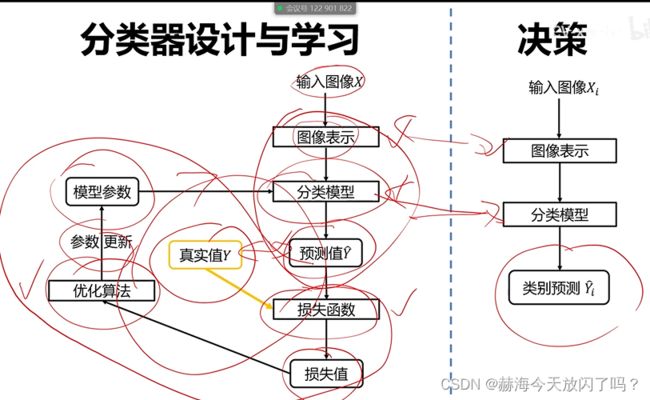
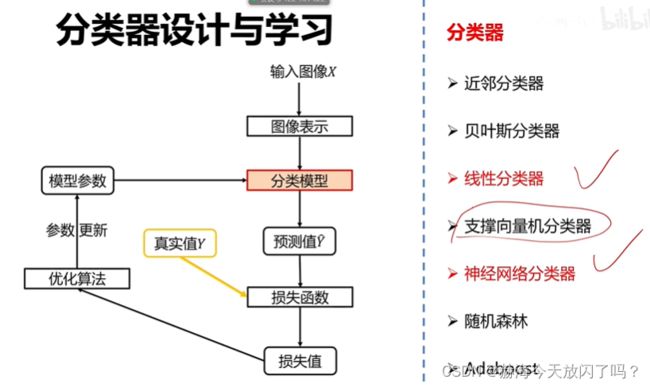
2)分类器
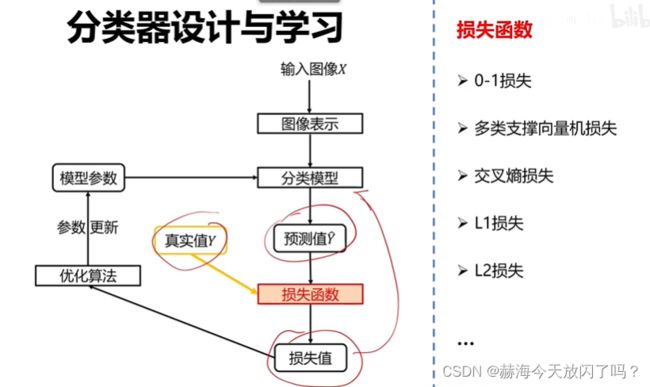
3)损失函数
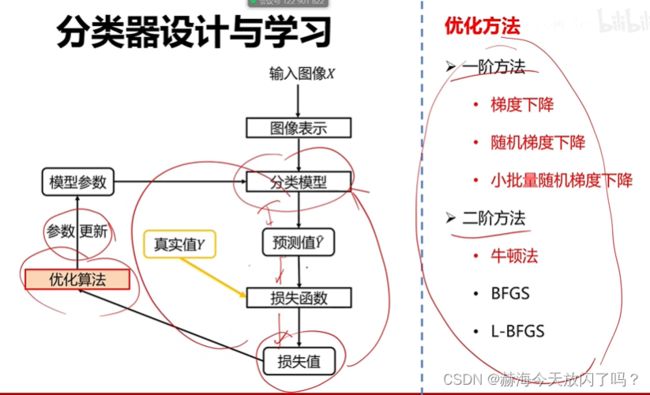
4)优化算法
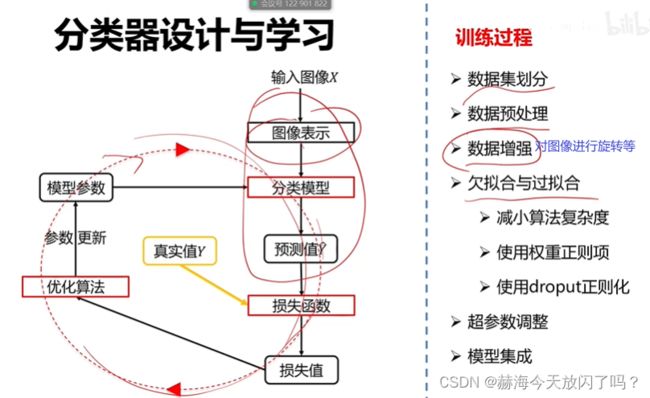
5. 常用的评价指标
第3章 线性分类器
1. 基本介绍
1)数据集
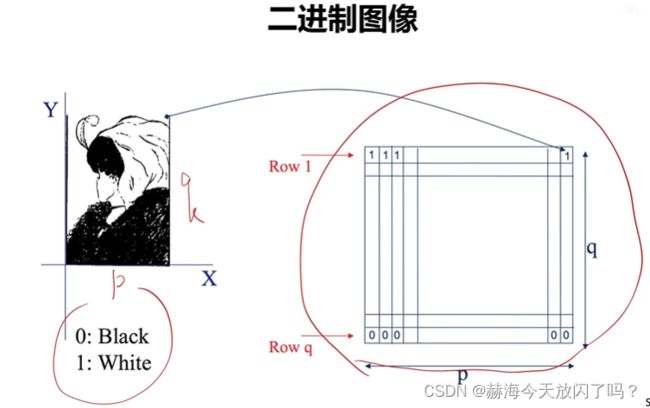
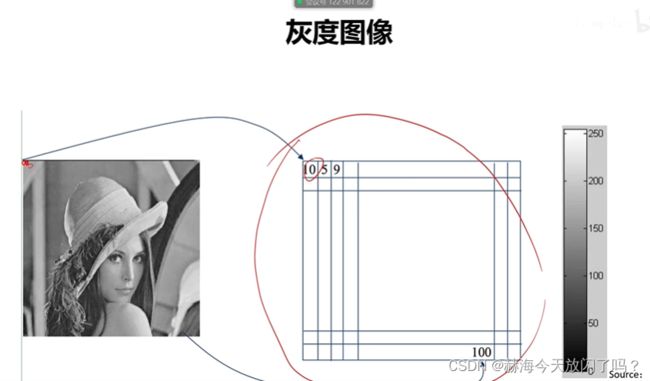
2)图像类型
3)图像表示
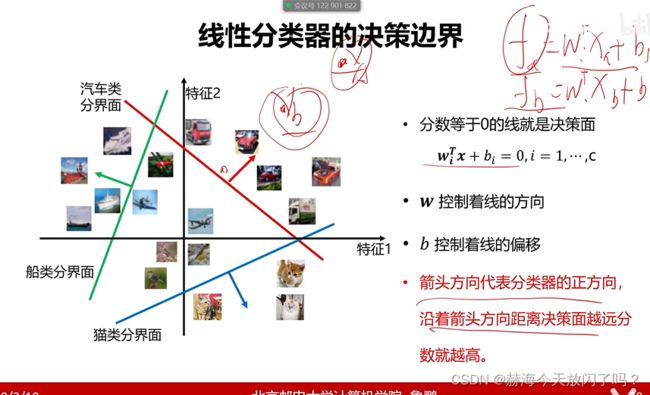
5)什么是线性分类器
6)举例说明

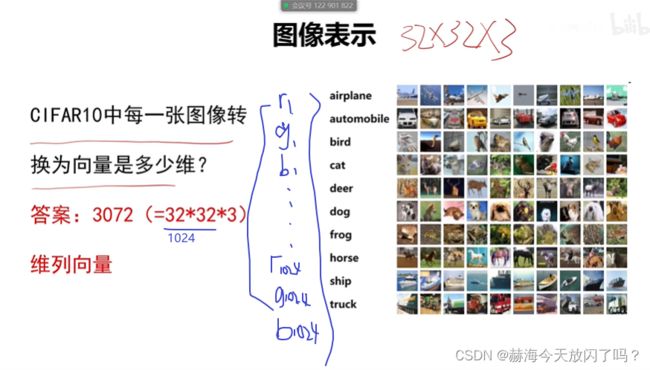
假设这个图片只有四个像素点,还都是灰度,只有一个通道的,展成列向量:
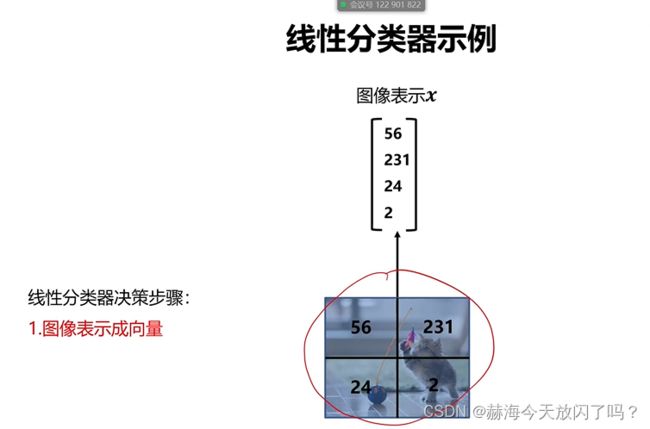

权值W的行数由类别数量确定,列数由像素点数量确定。
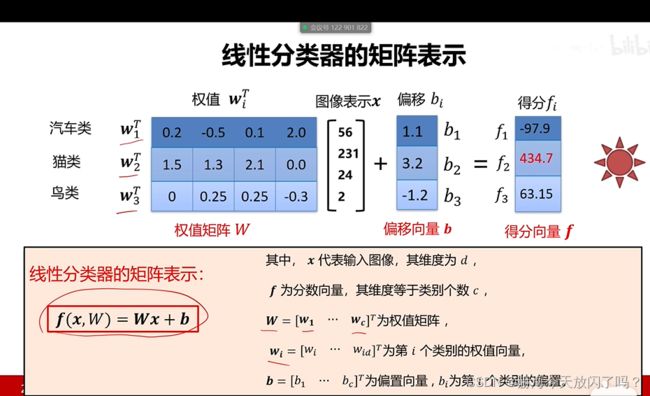

2. 细节理解
1)权值向量
继续上面的例子,我们的权值W是103072维的矩阵,可以将每个类对应的权值向量变成图像形式,3072=3232*3,发现权值向量的图片就像是每个类的模板一样:

为什么输入的图片和权值图片越相似,即向量值越相同输出的分数就越高?
两个向量点乘|c|=|a×b|=|a||b|cos
2)如何衡量分类器对当前样本的效果好坏?
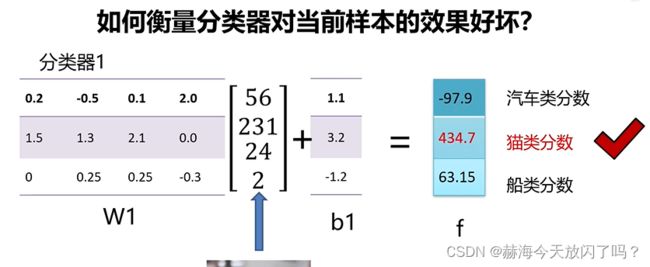
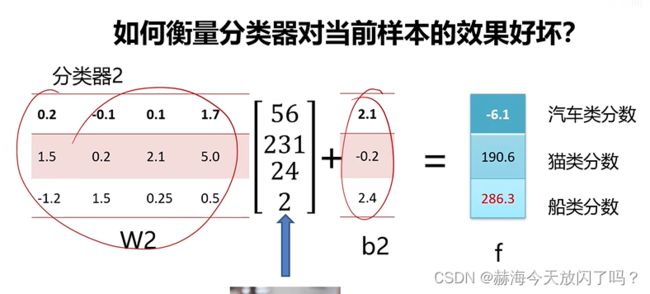
两个不一样的分类器,权值不一样,第一个分类正确,第二个分类不正确。分类器2的效果差。可是如何定量表示呢?需要损失函数。


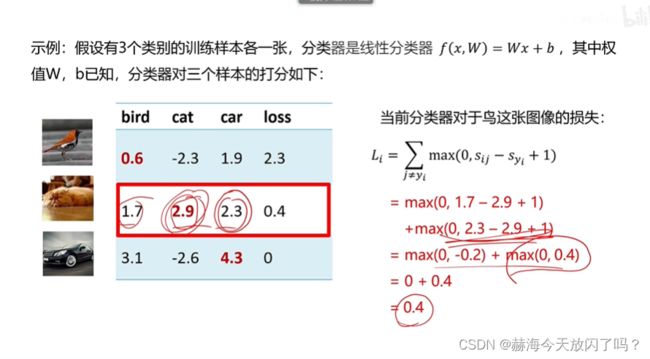
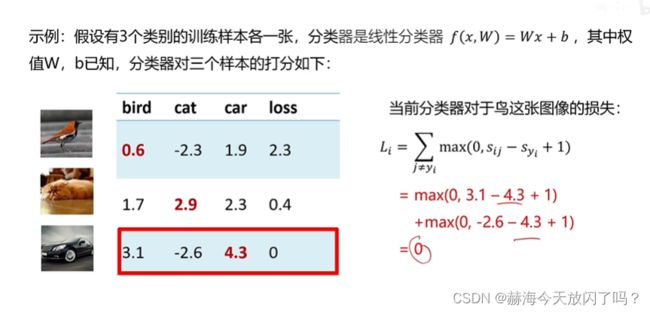
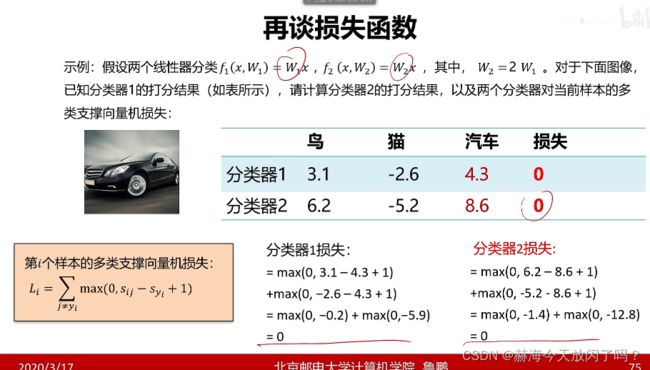
3)多类支撑向量机损失
+1只是为了不要太靠近边界,避免噪声。你也可以高两分,但没必要,这个东西只是为了防止有些图片处于决策边界,难以划分类别,所以干脆加一分,我再来看它有没有损失。
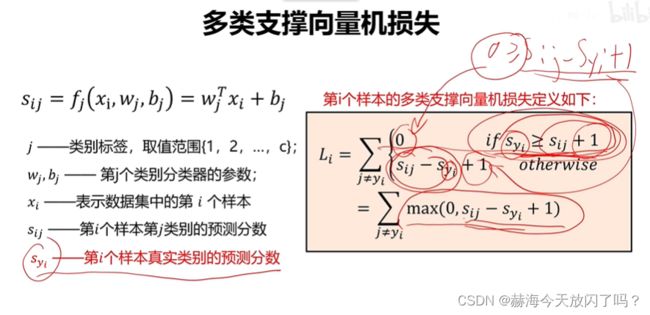

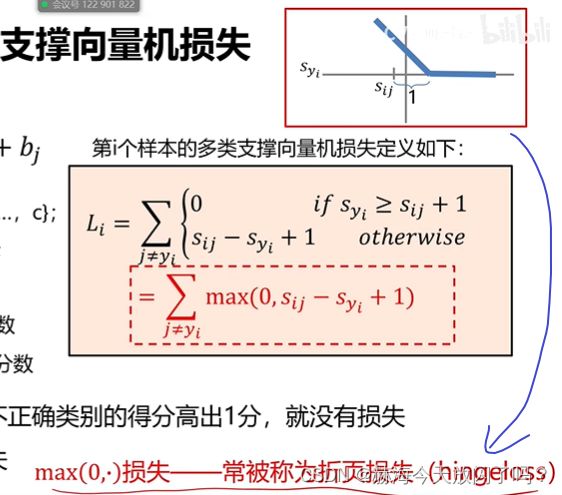
这个折页函数看法是这样的:
S y i S_{yi} Syi是变量,设 S i j S_{ij} Sij的位置固定,然后加上1,如果 S y i S_{yi} Syi比 S i j + 1 S_{ij}+1 Sij+1要大,无论大多少,损失都为0,所以后面的线就在横轴上了;如果 S y i S_{yi} Syi比 S i j + 1 S_{ij}+1 Sij+1要小,小越多损失越大。

3. 损失函数
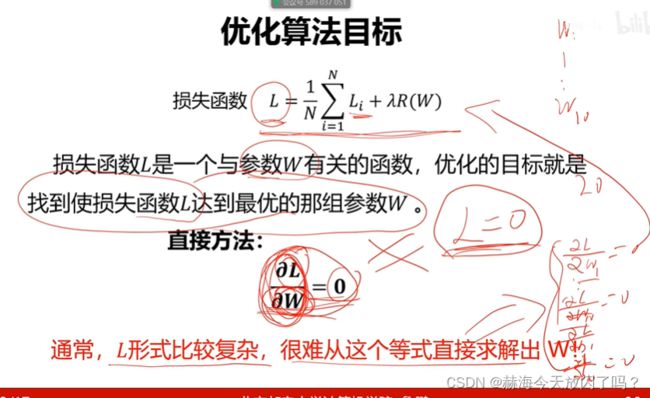
1)什么是损失函数?
损失函数其实就是在度量我当前参数的性能怎么样,因为分类模型已经确定了,改也只是改参数。损失函数一定要跟模型参数有关,不然没有意义!
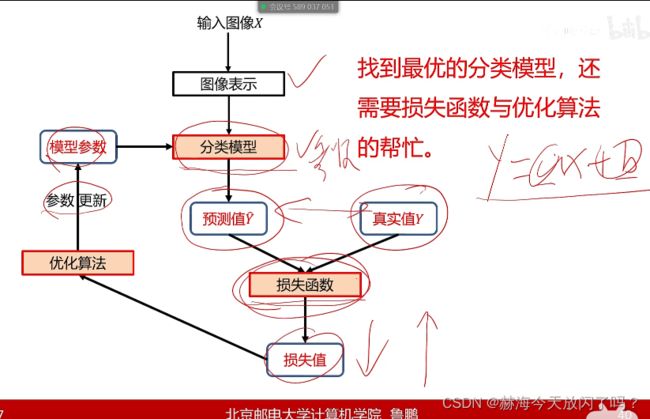

 A1:最小值毫无疑问就是0,最大值的话可以是无穷。
A1:最小值毫无疑问就是0,最大值的话可以是无穷。
A2:如果w和b很小,那么 S i j S_{ij} Sij和 S y i S_{yi} Syi都趋近于0, S i j − S y i = 0 S_{ij}-S_{yi}=0 Sij−Syi=0, m a x ( 0 , S i j − S y i + 1 ) = 1 max(0,S_{ij}-S_{yi}+1)=1 max(0,Sij−Syi+1)=1,如果有10个类,100张样本图片, L i = 9 L_{i}=9 Li=9则损失L会是 L = 1 N ∑ i L i ( f ( x i , W ) , y i ) = 1 100 ∗ 100 ∗ 9 = 9 L=\frac{1}{N}\sum_{i}L_{i}(f(x_{i},W),y_{i}) = \frac{1}{100}*100*9=9 L=N1∑iLi(f(xi,W),yi)=1001∗100∗9=9。
这个也可以用来检测编码正不正确,如果代码正确的话,w,b很小的时候,损失L的值应该等于类别-1。
A3:总损失多1
A4:放大N倍,不影响总结果,大家都放大了。
A5:对最后的结果是有影响的,损失大的占的比重就越大了。
2)正则项与超参数

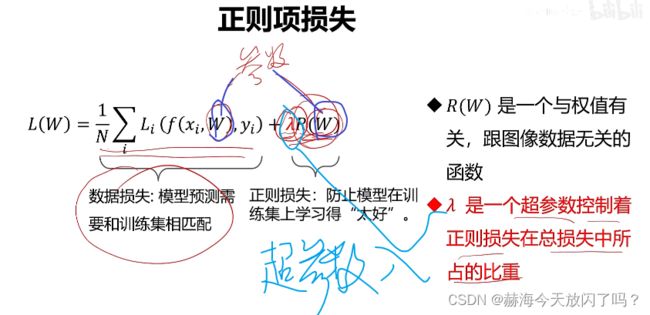
通过引入正则项解决这个问题:

参数是学习得到的,超参数是我们给定的。超参数其实是对模型性能来说很重要的,但是我们又不能真的一个个去调,所以怎么选好参数就很重要了,让我们成了炼丹侠。
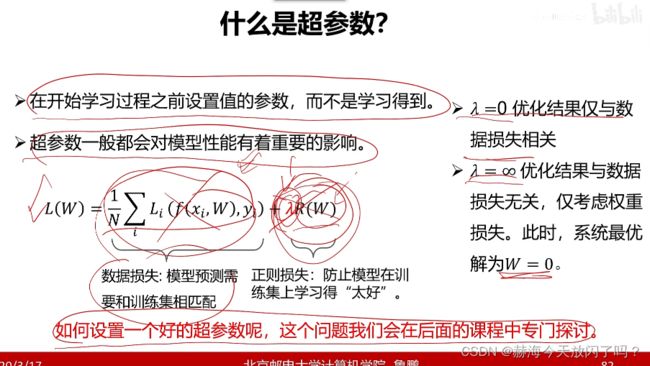

![]()
4. 优化
1)什么是参数优化?
2)梯度下降算法
目标就是导数=0,千万不能忘记这一点!
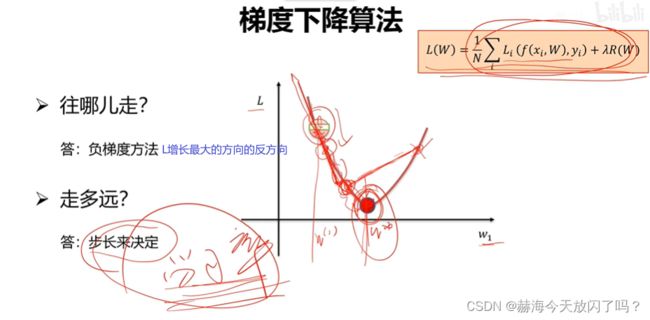




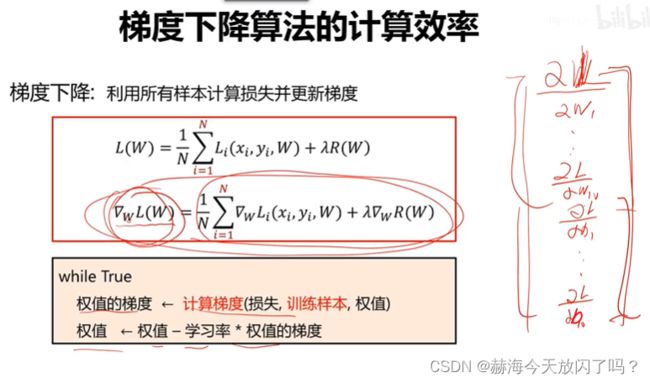
缺点,样本N很大的时候,权值的梯度计算量很大!因此有了随机梯度算法:

单个样本又可能使得结果不是每次都向着整体最优化方向走,因此有了batch



优化算法就是通过不断的迭代来调整权重参数,使损失降到最低。
5. 训练过程
1)数据集划分
![]()
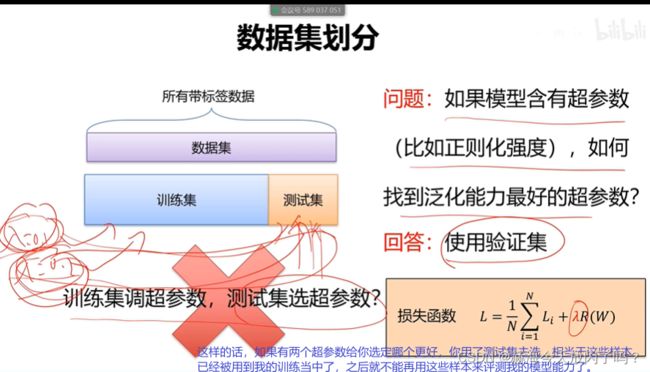
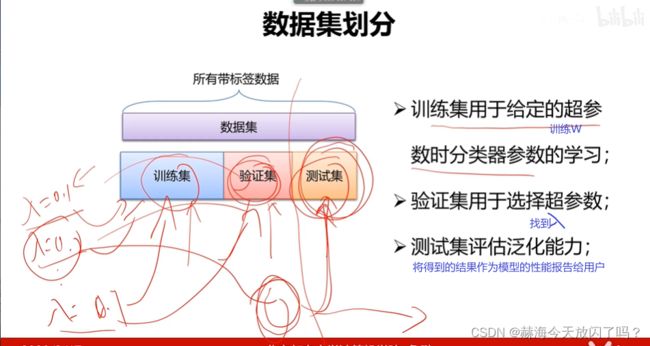
训练集上的参数选择是优化算法处理的,验证集上的超参数是人来选择的。
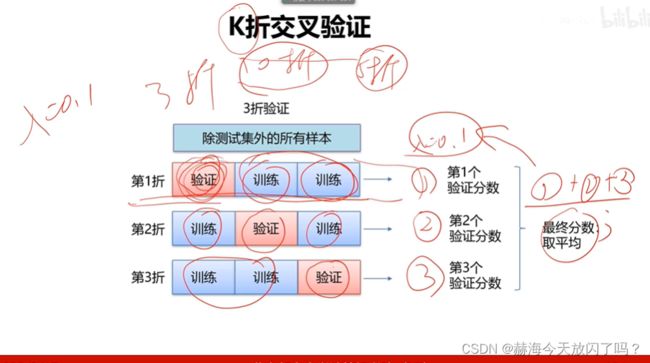
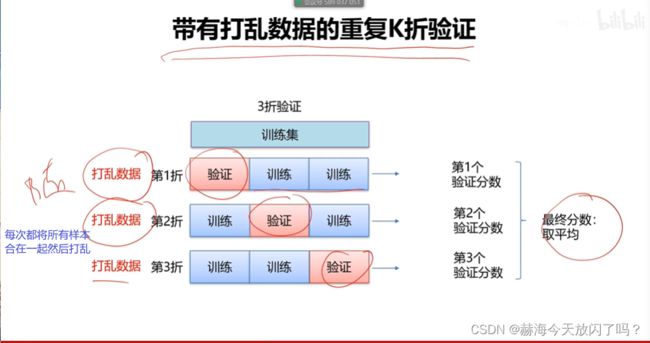
2)交叉验证
第4章 全连接神经网络
1. 多层感知器


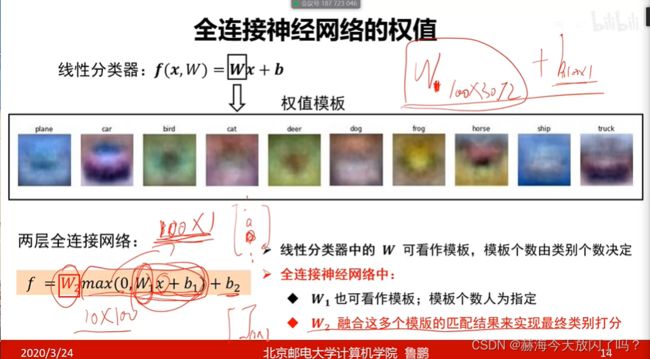
来继续分析一下这个,很关键!以我们一直以来常用的cifar10举例。

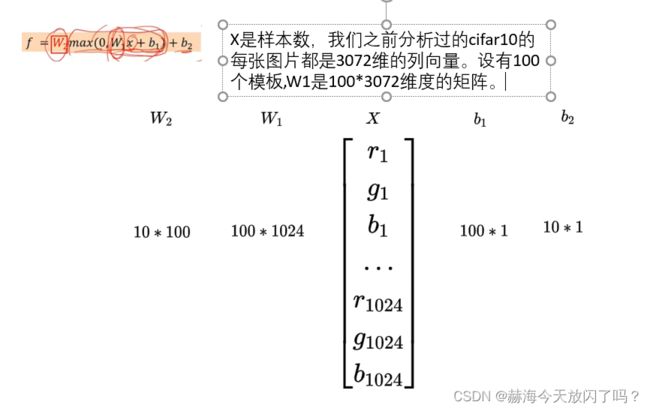

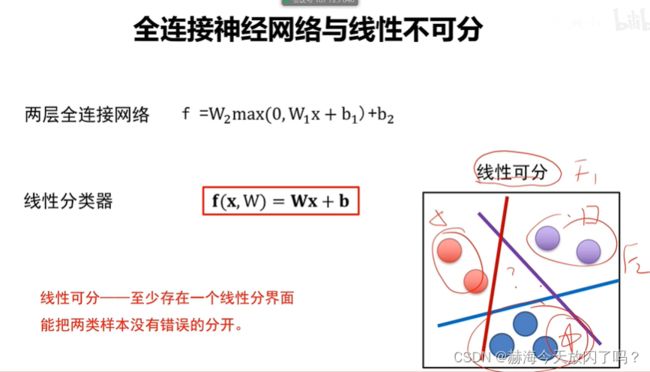
非线性可分要用全连接网络了

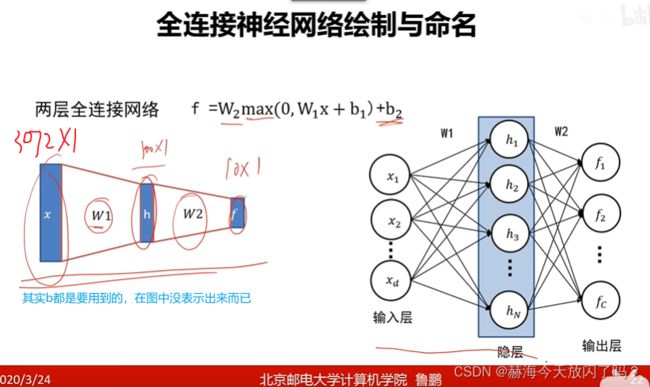
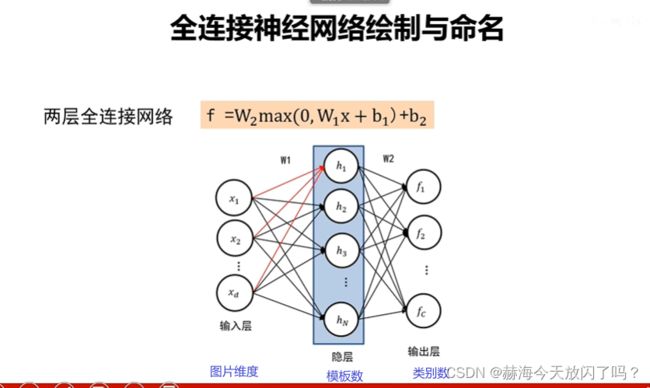
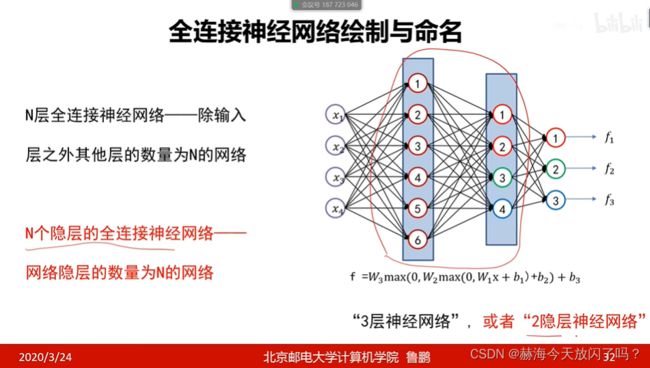
2. 激活函数

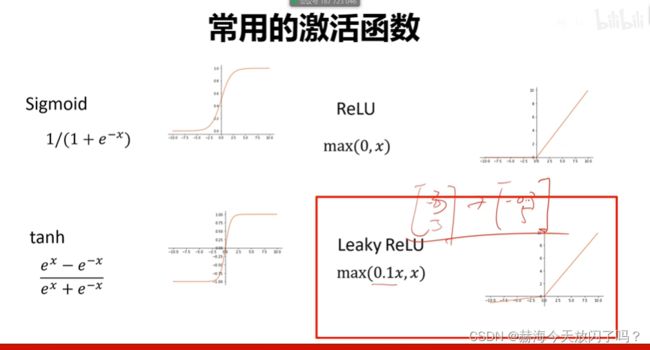

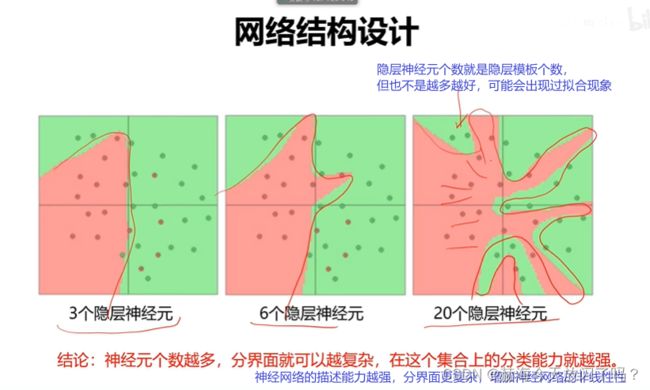
神经元越多,非线性越强,能描述更复杂的边界。让系统变得非线性更强的方法有两种:1.增加神经网络的深度,即神经网络的层数。2. 增加神经网络的宽度,即增加神经元的个数。主要还是增加深度,增加深度比增加宽度有效性更强,所以更加强调的是深度神经网络。


3. 损失函数
1)softmax
sofxmax的作用是让输出值范围在[0,1]之间,并且都为e的幂次方可以保证输出值恒大于0。e的次方可以将无论任何数字都转换成非负数(参考 e x e_{x} ex图像),然后再做归一化就是softmax的执行过程啦。
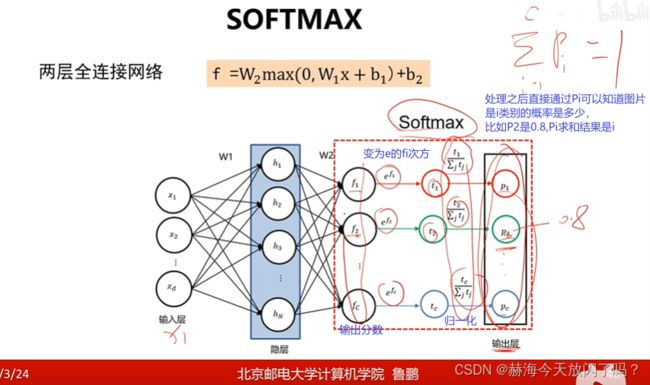

softmax能将神经网络的输出从那些绝对的数值变成概率。原来的系统只能告诉你,比如,“你答对了,分数是10000分”,经过softmax之后系统会告诉你,“你答对了,你的图片属于这个类的概率是0.8”
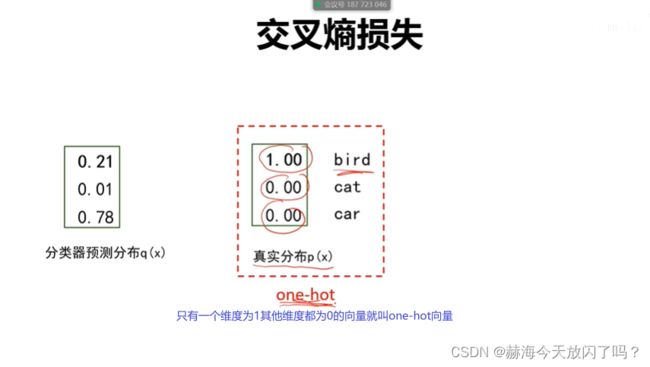
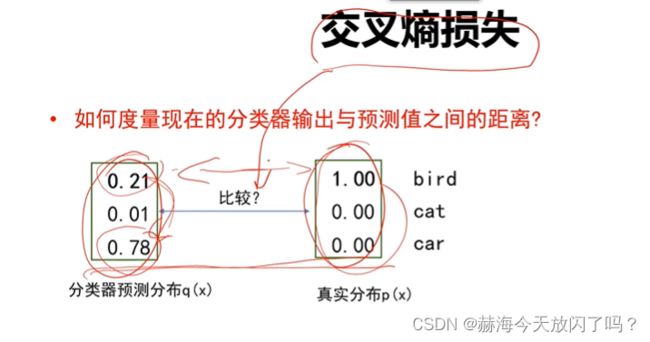
2)交叉熵损失
补充流畅输出那一段!!!!
真正用来度量的是KL散度,只是当标准答案是one-hot形式的时候交叉熵的值等于KL散度,可以用交叉熵替代KL散度去衡量这件事情。
3)对比多类支撑向量机损失
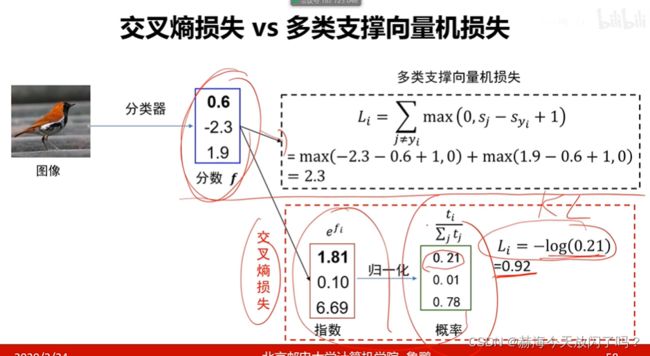
 交叉熵得出的结果还可以指导网络继续优化,我不止要让我自己概率最高,还让别的不正确的类的可能概率越低越好。而多类支撑向量机损失只要我比别人高1分就行了,不需要高很多。交叉熵损失关键就是我的概率不止要比别人大,还要比别人大很多。
交叉熵得出的结果还可以指导网络继续优化,我不止要让我自己概率最高,还让别的不正确的类的可能概率越低越好。而多类支撑向量机损失只要我比别人高1分就行了,不需要高很多。交叉熵损失关键就是我的概率不止要比别人大,还要比别人大很多。
4. 优化算法
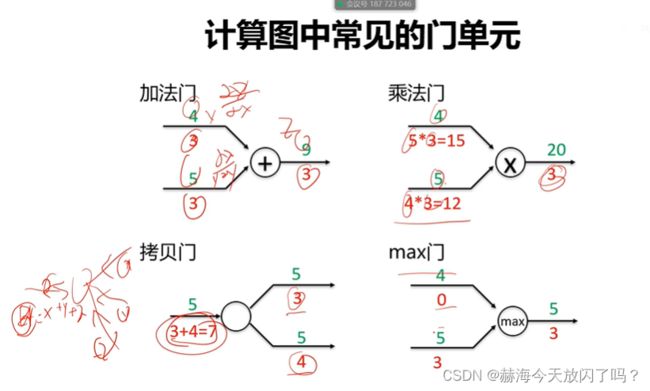
1)计算图和反向传播

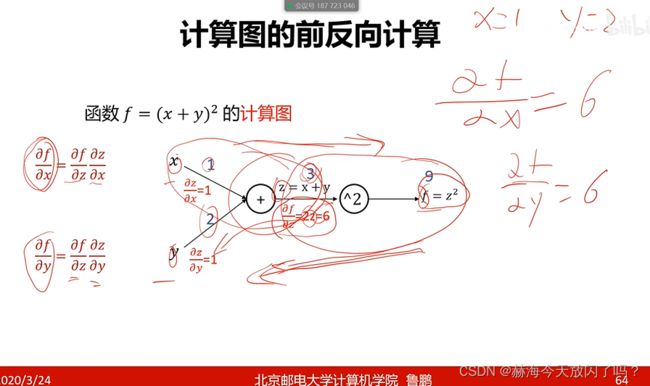

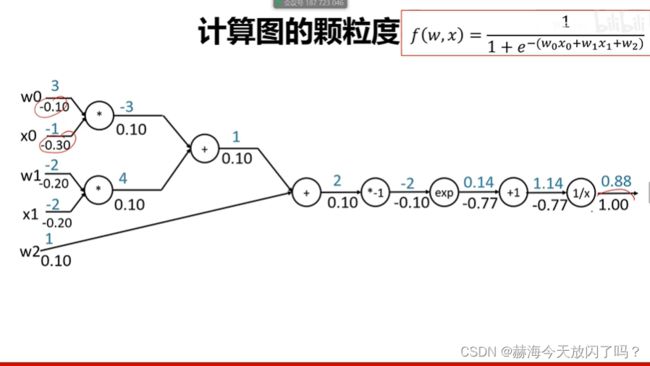

梯度消失:如果梯度小,因为链式法则都是偏导继续相乘的,越乘越小的话就会出现梯度传到中间已经没了的情况。
正向就可以任意一个点找到它的输出,反向就可以任意一个点找到它的梯度。
还可以这样算:
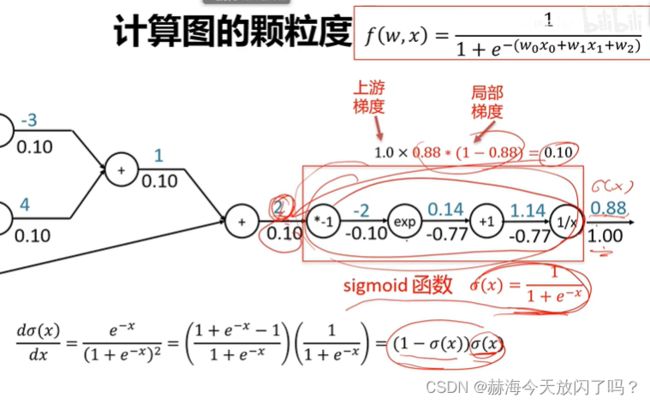
这就引出了一个颗粒度的问题,到底是要分开来一步步算呢还是合成一个比如上面的sigmoid函数然后快速求呢?用sigmoid的话是函数颗粒大但是也计算速度快。但是,如果你要速度快,不希望一步步分开求解,你就需要先把这些函数定义出来,把它们的导数求出来,写入到计算模块中。caffe就是用这样的,可以自己列式,速度快,但是要求你自己去写这个函数;tensorflow就是不用你写这些,全部都是用这种低颗粒度的一步步地去求,但是缺点就是速度慢,计算效率比较低。
2)再谈激活函数
![]()
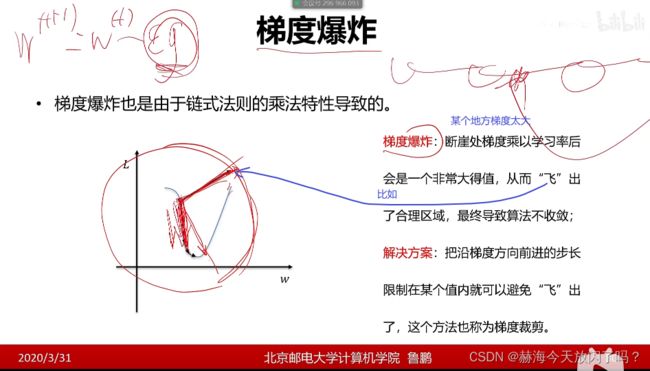
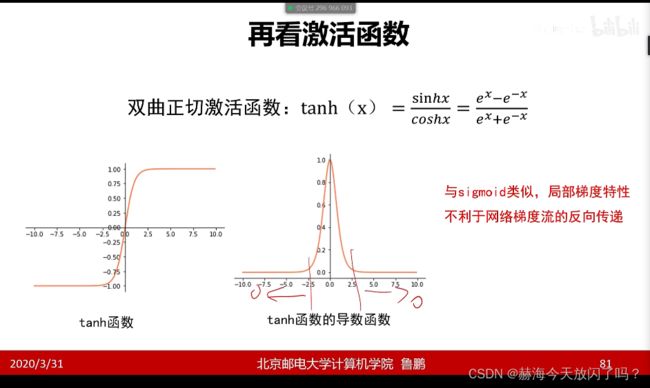
现在隐层已经很少用sigmoid、tanh这些了,用Relu即我们说的max
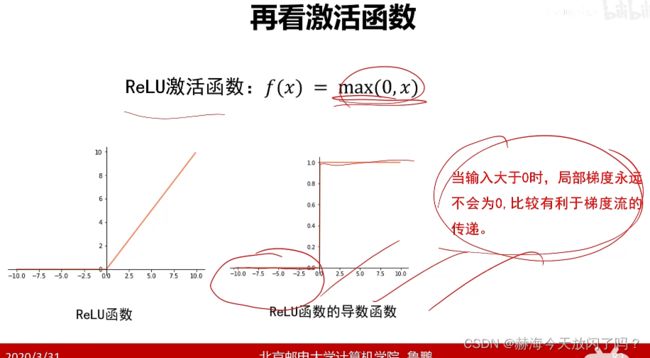
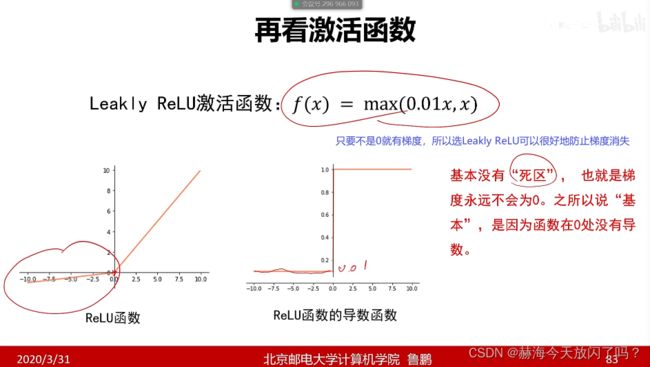
5. 梯度算法改进
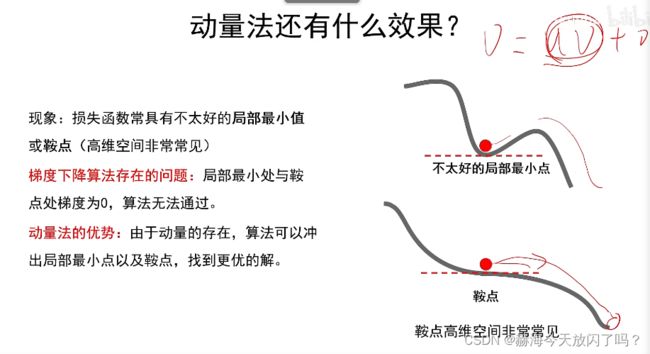
1)动量法
2)自适应梯度与RMSProp


不同地方不同学习率,平坦方向走快点,梯度大的震荡方向走慢点。

r越大越陡

动量法是通过此消彼长的感觉,自适应是在不同方向迈不同步子大小的感觉
推荐使用Adam或者SGD+动量,手动调整(SGD+动量)的学习率得到的效果会比adam好(炼丹),但是adam在很多情况下都可以用,不用怎么调。反正普遍就用这两种。
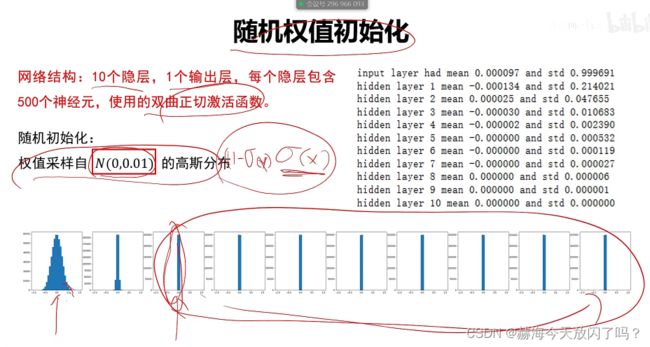
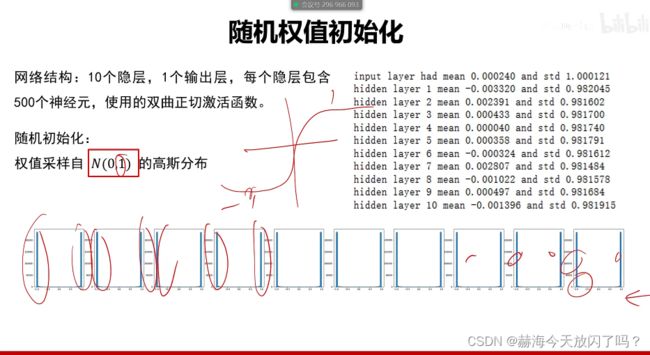
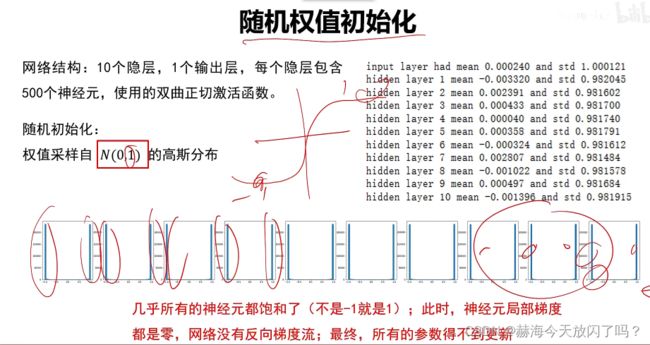
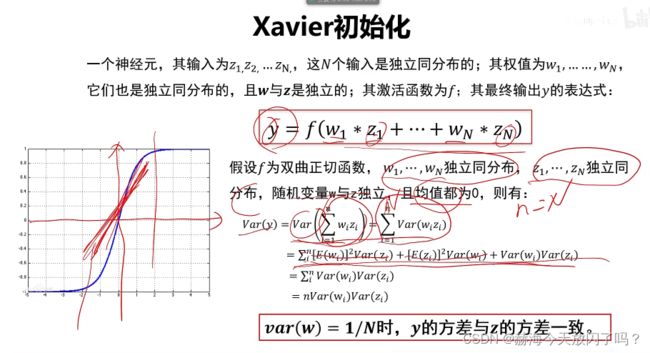
6. 权值初始化
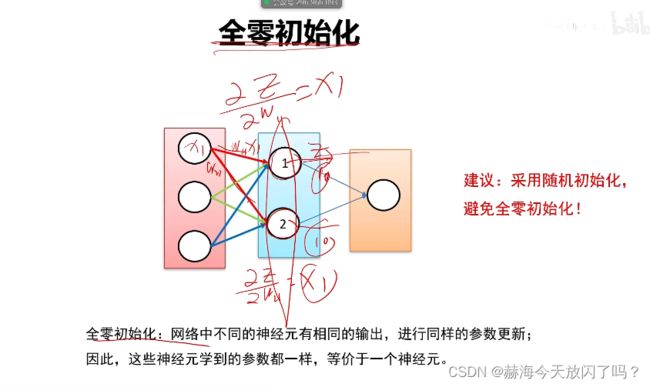
1)全零初始化(×)
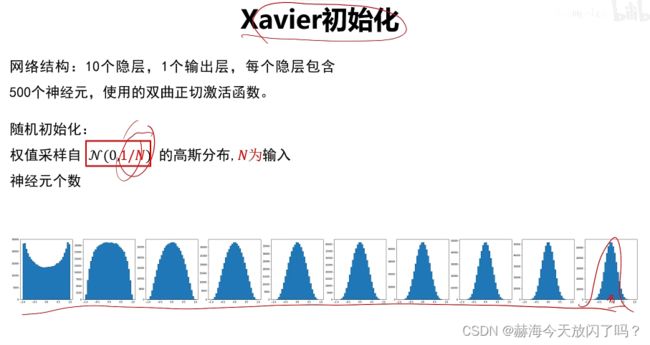
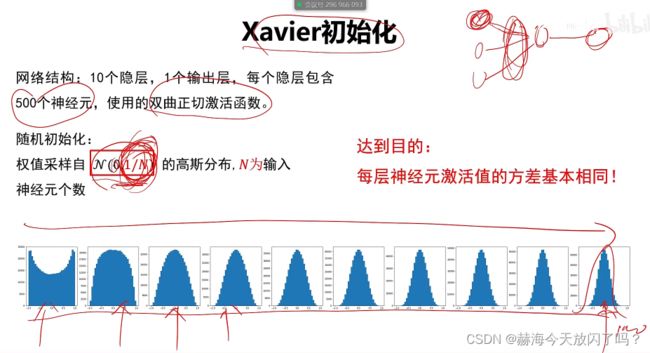
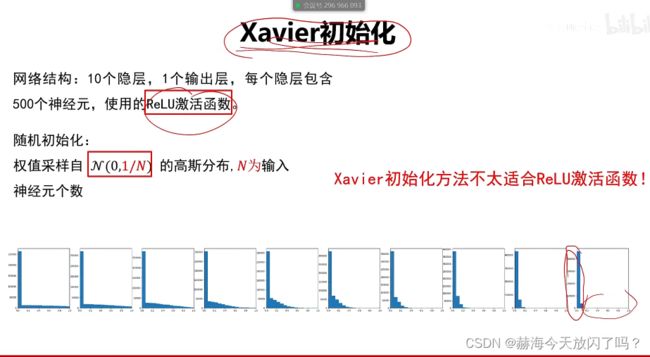
2)随机初始化
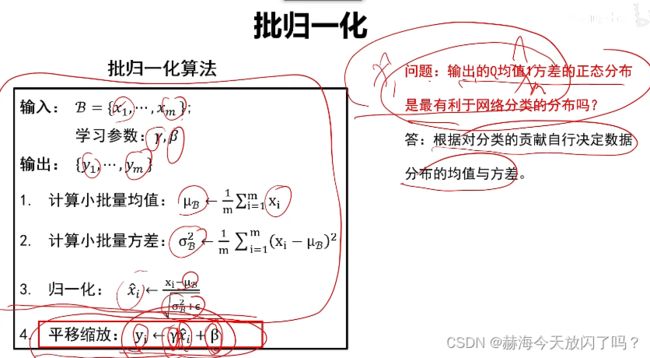
7. 批归一化
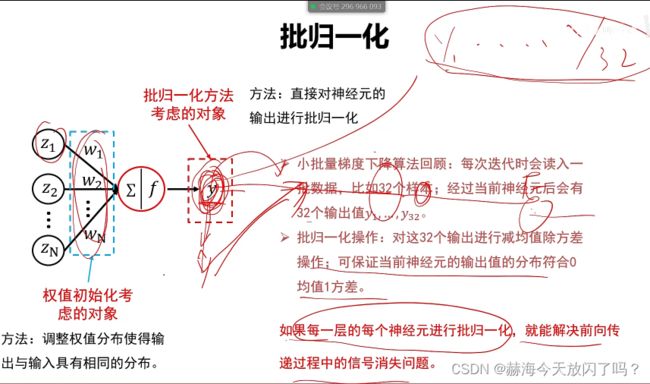
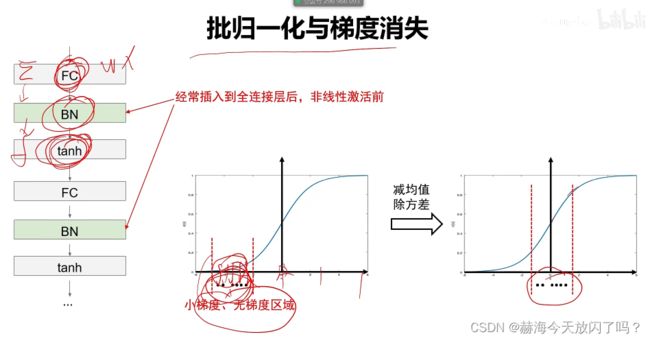
批归一化1保证了前向传递能够往前传2能保证梯度不会消失
FC是全连接层,BN是批归一化,tanh激活函数


8. 过拟合

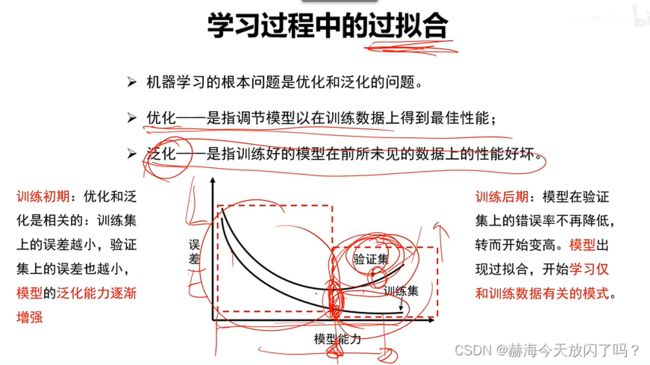

如果能有很多的数据,直接把所有数据记下来就行,这样就是最优的方案了。

L2正则会把方差抹平,所以很极端的曲线不可能出现
极端曲线如下,就是一个一个去圈,不是用平滑的曲线作为分界面。
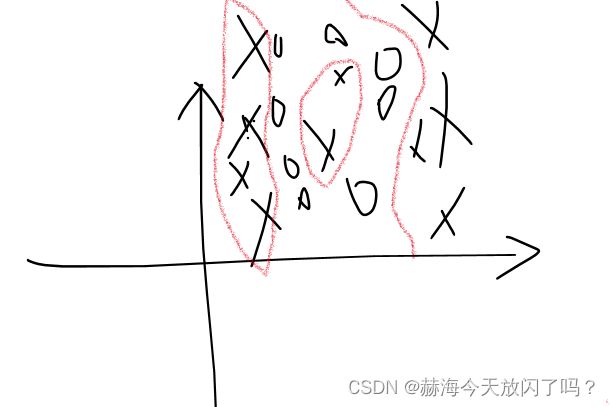


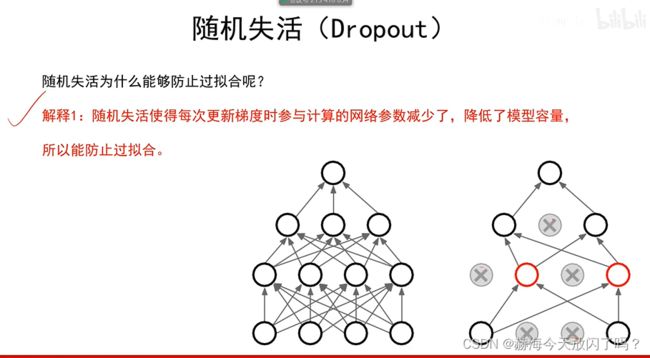
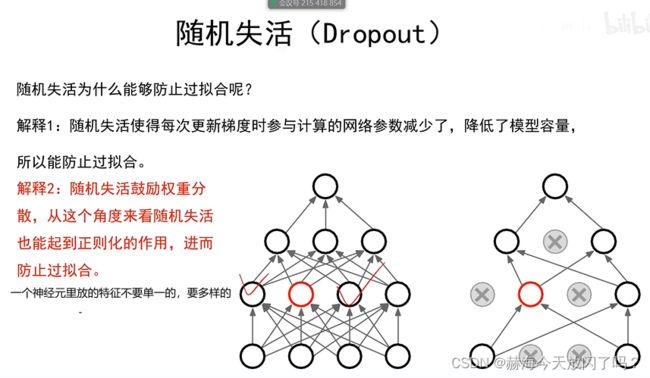
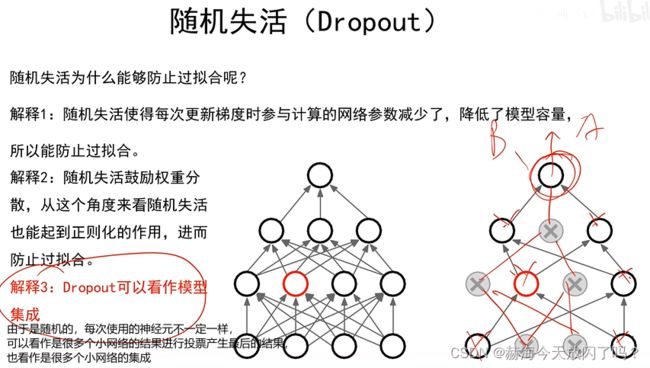
集成模型的鲁棒性很好。
第5章 卷积


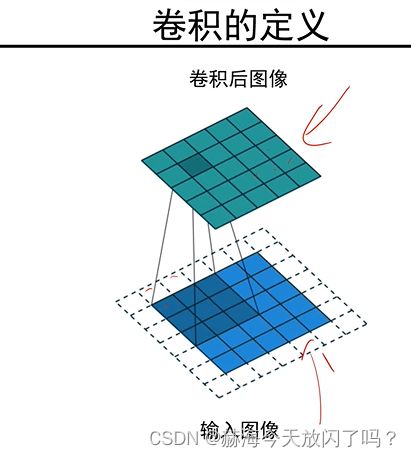
这个过程就叫做对图像中的一个点进行了一次卷积操作


![]()
平移后卷积和卷积后平移是一样的


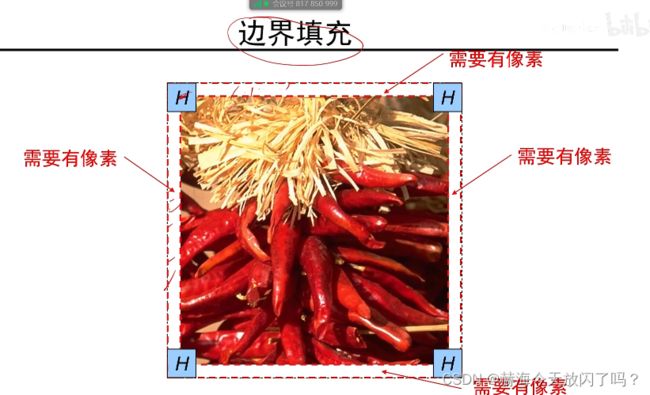
如果不填充,卷积出来的图像会比原来的小
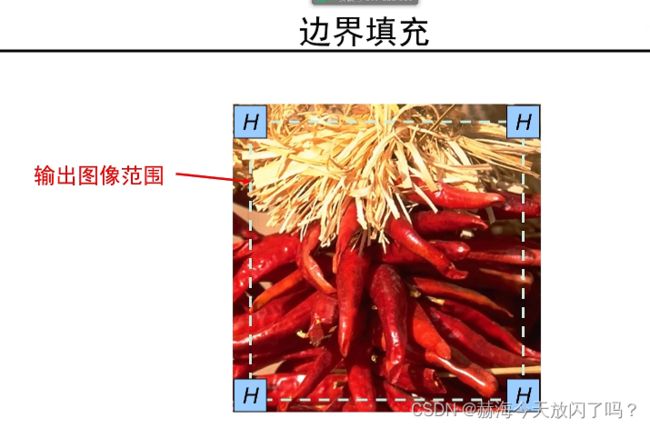
常用零填充

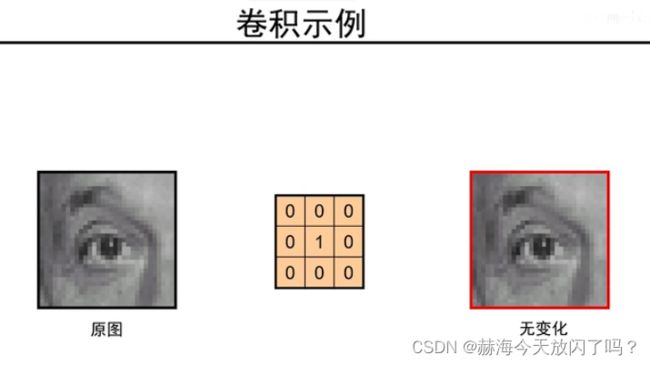
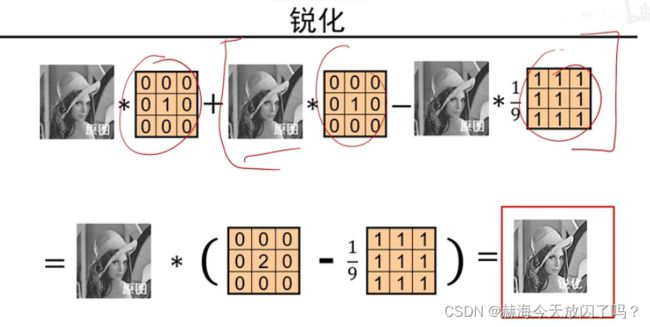
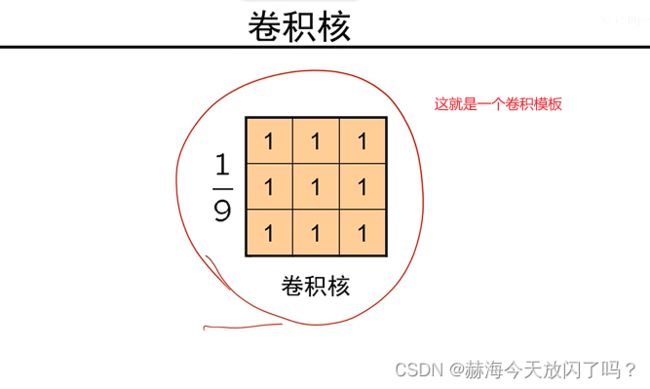
为什么不是都变成原来的1/9?此卷积非彼卷积,一般图像处理中的卷积求和都是要除以尺寸的,而CNN就是直接求和,所以不变没毛病。没有平均操作。
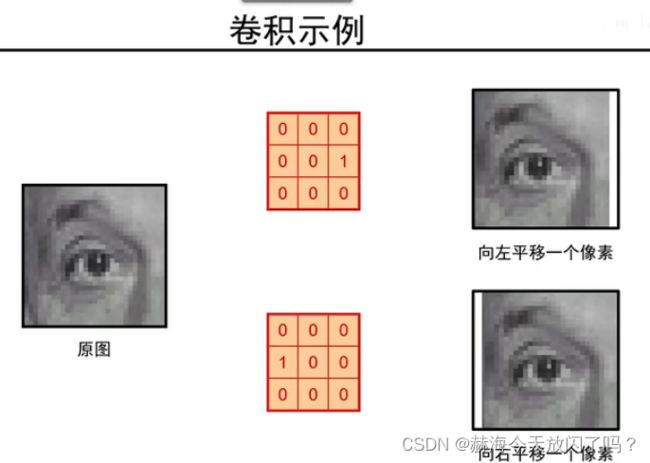
从这也可以看出卷积可以实现平移操作
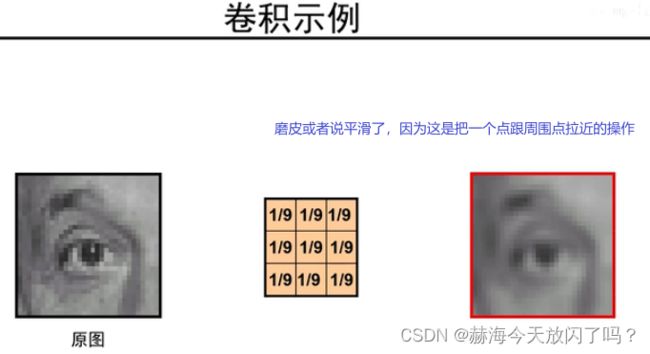
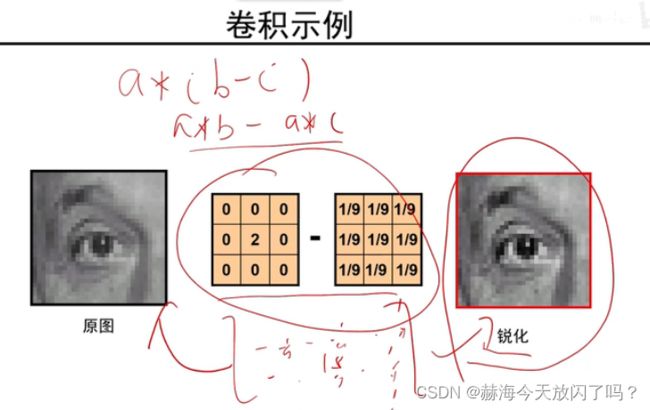
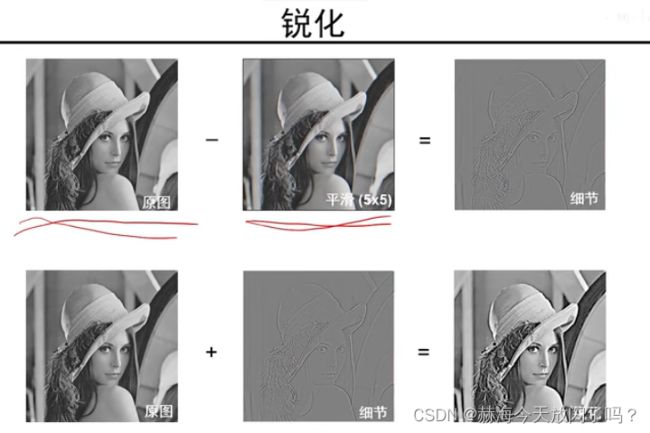
原图减平滑图得到边缘图,比如一个点是250,减去1/9的卷积平滑图之后,剩下的是这个点非常显著的特征了。再用原图加细节特征,我们就可以得到锐化后的图片。