自动驾驶系列(二) - 路径规划五种算法简述及对比

• 个人主页: 同学来啦
• 版权: 本文由【同学来啦】原创、在CSDN首发、需要转载请联系博主
• 如果文章对你有帮助，欢迎关注、点赞、收藏和订阅专栏哦

一、引言

路径规划部分在无人车架构体系当中分属控制或决策部分，是实现无人化驾驶的关键技术之一。路径规划模块性能的高低直接关系车辆行驶路径选择的优劣和行驶的流畅度，而路径规划算法的性能优劣很大程度上取决于规划算法的优劣。如何在各种场景下迅速、准确地规划出一条高效路径且使其具备应对场景动态变化的能力是路径规划算法应当解决的问题。

根据对环境信息的把握程度可把路径规划划分为基于环境先验完全信息的全局路径规划和基于传感器信息的局部路径规划。其中，从获取障碍物信息是静态或是动态的角度看，全局路径规划属于静态规划，局部路径规划属于动态规划。全局路径规划需要掌握所有的环境信息，根据环境地图的所有信息进行路径规划；局部路径规划只需要由传感器实时采集环境信息，了解环境地图信息，然后确定出所在地图的位置及其局部的障碍物分布情况，从而可以选出从当前结点到某一子目标结点的最优路径。

在全局路径规划算法中，大致可分为三类：传统算法（Dijkstra算法、A*算法等）、智能算法（PSO算法、遗传算法、强化学习等）、传统与智能相结合的算法。智能算法种类繁多，但传统算法更为基础，故本着由浅入深的原则，首先对传统算法展开介绍。

二、算法综述

在传统路径规划算法中，各种算法的实现原理和应用范围差异很大，但可以将以下五种算法看作一类（Dijkstra、A*、D*、 LPA*、D* Lite），以下对各算法的基本原理进行阐述，并在搜索原理和应用场景等方面进行了对比区分。

1、算法介绍

1.1 Dijkstra 算法

Dijkstra算法是由E.W.Dijkstra于1959年提出，又叫迪杰斯特拉算法。该算法采用了一种贪心模式，其解决的是有向图中单个节点到另一节点的最短路径问题，其主要特点是每次迭代时选择的下一个节点是当前节点最近的子节点，也就是说每一次迭代行进的路程是最短的。为了保证最终搜寻到的路径最短，在每一次迭代过程中，都要对起始节点到所有遍历到的点之间的最短路径进行更新，实现流程如下：

• ①初始化：
  建立distance[ ]（起点到其他所有点的距离信息）、Top_node[ ]（最短路径信息）两个列表存放信息。其中，distance[ ]的维度为节点的个数，每一个数值为到达对应索节点的最短路径距离，比如distance[2]的值代表当前迭代时刻到达3号节点的最短距离。初始状态[distance 0 inf 10 inf 30 100]，其中0代表自身，inf代表无法到达；Top_node[num1]，其中num1代表1号节点并以此类推。
• ②搜索最小点：
  找到当前节点到下一点的最小值，即从num1开始搜索到1->3/1->5/1->6三条路径，并找出距离最短的路径，可以发现此时到达num3点的最短路径长度为10，则将num3存入Top_node[ ]。
• ③松弛：
  确定num3找到最短路径，然后num3开始搜寻其弧尾，找到3->4路径，此时1->3->4路径距离为10+50=60，小于inf，故将列表更新为distance[0 inf 10 60 30 100]。注意这里通过3->4路径来缩短1->4路径的过程叫做“松弛”，该算法证实通过这样的方法能够进行路径寻优。
• ④重复迭代:
  除去num1和num3，从剩余点搜寻距离最短的节点，进一步可以确定为num5节点，故将num5加入Top_node[ ]。找到弧尾路径5->4/5->6,进行松弛，其中 1->5->4距离为30+20=50<60，1~>5->6距离为30+60=90<100，所以列表更新为distance[0 inf 10 50 30 90]。
• ⑤重复迭代:
  除去numl、num3和num5，其余点搜寻距离最短的路径，确定为num4节点，将其加入Top_node[ ]。然后找到弧尾4->6，进行松弛，1->5->4->6距离为30+20+10=60<90，1->3->4->6距离为10+50+10=70>60，进行列表更新distance[0 inf 10 50 30 60]。

以上就是Dijkstra算法的简单实例，可见其主要是通过贪心原则逐个遍历最小子节点，然后利用松弛方法去优化路径选择，最终将最优路径存放到可读列表当中，以此来解决最优路径规划问题。

1.2 A*算法

A*算法是启发式搜索算法，启发式搜索即在搜索过程中建立启发式搜索规则，以此来衡量实时搜索位置和目标位置的距离关系，使搜索方向优先朝向目标点所处位置的方向，最终达到提高搜索效率的效果。
A*的算法的基本思想如下：引入当前节点x的估计函数$f(x)$，当前节点x的估计函数定义为：
$f(x)=g(x)+h(x)$
其中g(x)是从起点到当前节点x的实际距离量度（代码中可以用两点之间距离代替）；$h(x)$是从节点x到终点的最小距离估计，$h(x)$的形式可以从欧几里得距离$(\sqrt{(x-x_i{)}^2+(y-y_i{)}^2})$或者曼哈顿距离$(|x-x_i|+|y-y_i|)$
算法基本实现过程为．从起始点开始计算其每一个子节点的f值，从中选择f值最小的子节点作为搜索的下一点，往复迭代，直到下一子节点为目标点。

1.3 D*算法

基于算法，Anthony Stentz在1994年提出了Dynamic A算法，也就是D算法。D*算法是一种反向增量式搜索算法，反向即算法从目标点开始向起点逐步搜索；增量式搜索，即算法在搜索过程中会计算每一个节点的距离度量信息$H(x)$，在动态环境中若出现障碍物无法继续沿预先路径搜索，算法会根据原先已经得到的每个点的距离度量信息在当前状态点进行路径再规划，无需从目标点进行重新规划。
其中，距离度量信息$H(x)=H(y)+C(y,x)$，$H(y)$代表点到目标点的距离度量，$C(y,x)$代表y点到x点的距离度量，在算法中均可用两点间实际距离代替。

1.4 LPA*算法

2001年，由斯文·柯尼格（Sven Koenig)和马克西姆·利卡切夫（Maxim Likhachev)共同提出的Life Planning A*算法是一种基于A*算法的增量启发式搜索算法。
LPA*算法实现原理：
搜索起始点为所设起点（正向搜索），按照Key值的大小作为搜索前进的原则，迭代到目标点为下一搜索点时完成规划；Key值中包含启发式函数h项作为启发原则来影响搜索方向；处于动态环境时，LPA*可以适应环境中障碍物的变化而无需重新计算整个环境，方法是在当前搜索期间二次利用先前搜索得到的$g$值，以便重新规划路径。

其中，Key[]为一个二维数组：
$k(n)$=$\left[\begin{array}{c}{k}_1(n)\\ k_2(n)\end{array}\right]$=$\left[\begin{array}{c}min(g(n),rhs(n))+h(n,goal)\\ min(g(n),rhs(n))\end{array}\right]$

$g(n)$代表起点到当前点的距离度量。$rhs(n)$为$min(g(n^{\prime })+c(n^{\prime },n))$, n’为n的父节点，$h(n,goal)$为启发项；搜索原则为：优先判断$k_1$大小，若$k_1$小则优先遍历，若$k_1=k_2$，则选择$k_2$较小的点。

1.5 D* Lite算法

D* Lite算法是Koenig S和Likhachev M基于LPA*算法基础上提出的路径规划算法。D* Lite与LPA*的主要区别在于搜索方向的不同，这就将Key[]定义中涉及到的目标点goal替换为起始点start的相应信息。
D* Lite算法是先在给定的地图集中逆向搜索并找到一条最优路径。在其接近目标点的过程中，通过在局部范围的搜索去应对动态障碍点的出现。增量式算法的优势在于：各个点的路径搜索己经完成，在遇到障碍点无法继续按照原路径进行逼近时，通过增量搜索的数据再利用直接在受阻碍的当前位置重新规划岀一条最优路径，然后继续前进。

2、算法比较

2.1 算法性能

算法	搜索方向	启发式	增量式	适用范围	现实应用
Dijkstra	正向搜索	否	否	全局信息已知，静态规划	网络通信中的最短路由选择
A*	正向搜索	是	否	全局信息已知，静态规划	Apollo、游戏、无人机路径规划
D*	反向搜索	否	是	部分信息已知，静态规划	机器人探路、火星探测车路径规划
LPA*	正向搜索	否	是	部分信息已知，假设其余为自由通路，动态规划	机器人路径规划
D* Lite	反向搜索	是	是	部分信息已知，假设其余为自由通路，动态规划	机器人路径规划

上表中给出了五种算法分别在搜索方向、启发式、增量式、适用范围和现实应用五个方面的对比。以上五种算法的效能和适用范围各不相同，效能高且解决问题范围广并不一定代表应用广泛，目前实际应用的算法应偏向竭力发挥某一算法的专长，在基础功能之上不断优化算法性能。

2.2 要点理解

• 搜索方向的正反：
  在静态环境中全局地图信息己知，则无论正向搜索还是反向搜索都可以发挥效能。但是在动态环境中，面对未知地图，要想获得最短路径则需要不断的尝试，正向搜索很容易产生与最优路径背道而驰的现象，而此时反向搜索算法能够很好地处理这种情况。反向搜索配合增量式搜索使得D*Lite算法在动态障碍图中，可以利用先前迭代中产生的节点距离信息，不断更新当前点到目标点的最优路径。而在正向搜索中，增量式算法只能提供当前点到起始点的距离信息和到目标点的启发估计信息，并不能保证未搜索区域的可通行性。

• 启发式与非启发式：
  启发式算法能够在每次搜索时将搜索方向导向目标点，替代了非启发式算法向四周无规则遍历的局限，正常、青况下能够大大提高搜索效率。但是在启发式路径受阻的情况下，搜索效果将适得其反。
  

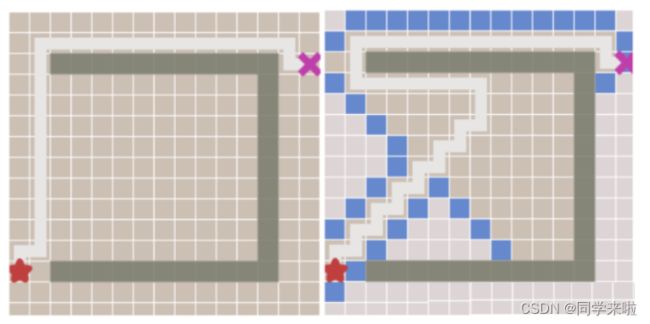
• 启发式与增量式：
  1）启发式搜索是利用启发函数来对搜索进行指导，从而实现高效的搜索，启发式搜索是一种智能搜索，典型的算法例如A*算法、遗传算法等。
  2）增量式搜索是对以前的搜索结果信息进行再利用来实现高效搜索，大大减少搜索范围和时间，典型的例如LPA*、D*Lite算法等。
  搜索方向的正反多与是否能处理动态规划有关；启发式搜索能带来效能的提高，有利于避免全局盲目搜寻，增量式搜索则代表着迭代信息的二次利用，多用于提高算法效率。