二元逻辑回归 · 数学推导过程及代码实现完全解析

---

最近修改：2021/6/17

原文《从二元逻辑回归到多元逻辑回归 · 推导过程完全解析》经过多次修改后变得越来越长，因此笔者将其分为两部分：

第一部分：二元逻辑回归 · 数学推导过程及代码实现完全解析
第二部分：多元逻辑回归 · 数学推导过程及代码实现完全解析

概述

以下是此篇文章要用的包

# 加载包
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('darkgrid')

两个重要函数

二元逻辑回归的出发点是sigmoid函数
$$S(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{1+e^x}$$

Sigmoid函数能将实数域的连续数映射到0,1区间，概率的取值范围就在0,1之间，因此可以用来做概率的预测。

以下是Sigmoid函数的代码和图像

x=np.arange(-10,10)
y=1/(1+np.exp(-x))
plt.plot(x,y)

Output:

多元逻辑回归的出发点是softmax函数
$$S(x)=\frac{e^{x_i}}{{\sum }_{j=1}^k{e}^{x_j}}$$
Softmax函数也是将实数域的连续数映射到0,1区间，进而可以理解为是概率。

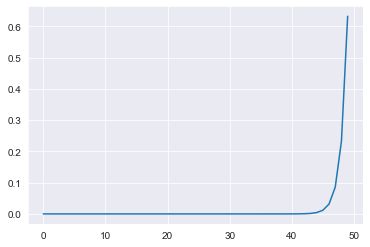
以下是softmax函数的代码和图像

图像的特点：

• 设向量x=[0,1,2,3,…,49]，其输出也是一个向量y
• 这里Softmax函数会将x里的每个数映射到0,1区间
• 并且y里元素加和为一
• 数越大，其输出也越大，即概率越大。

x=np.arange(0,50)
y=np.exp(x)/np.sum(np.exp(x))
plt.plot(x,y)
print('the sum of y={}'.format(y.sum()))

Output:
the sum of y=1.0

预测的基本思想

我们想处理分类问题，最基本的统计模型便是逻辑回归，之所以使用它，最主要的原因是其输出是在0,1之间。

注意，我们并不是直接输出类别编号，而是一个概率值

然后我们会根据情况的不同来确定一个阈值,通常这个阈值定在0.5。比如，二元模型中(类别0和1)，我的输出是P(Y=1)=0.75(0.75>0.5)，则认为此时Y是属于类别1的。

---

二元逻辑回归

线性模型的简单回顾

要解释二元逻辑回归，我们得先来了解下什么是线性模型

首先这个模型建立在两个个假设上

• 假设$y$和$X$之间是一个线性关系
• $y_i(i=1,2,3,...,n)$是独立同分布

$y$和$X$之间的线性关系

$$y=X\beta$$

因变量$y$是一个nx1向量

$$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right]$$

带截距项的自变量$X$是一个nx(m+1)的矩阵
$$X=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& ...& x_{1m}\\ 1& x_{21}& x_{21}& ...& x_{2m}\\ ⋮& ⋮& & ⋮& \\ 1& x_{n1}& x_{n2}& ...& x_{nm}\end{array}\right]$$

带截距项的参数$\beta$是一个mx1向量
$$\beta =\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_m\end{array}\right]$$

从线性回归到二元逻辑回归

对于二值因变量$y_i$($y_i=0$或$y_i=1$)，我们的假设是$y_i(i=1,2,...,n)$ 独立同分布Bernouli分布，即

$$y_i\sim Bernouli(P(y_i=1))$$
首先我们想到用最基本的线性回归来估计$y_i$，在Bernouli分布中，$y_i$的均值是$P(y_i=1)$，因此我们的预测模型为

$$E(y_i)=P(y_i=1)=x_i\beta$$

但这样做的缺点就是$x_i\beta$的取值可能会落在[0,1]之外，受Sigmoid函数的启发，我们将预测模型改成
$$E(y_i)=P(y_i=1)=\frac{1}{1+e^{-x_i\beta }}$$
$\beta =({\beta }_0,{\beta }_1,\dots {\beta }_m{)}^{\prime }，且x_i=(1,x_{i1},x_{i2},\dots ,x_{im})，即x_i\beta ={\beta }_0+x_{i1}{\beta }_1+...+x_{im}{\beta }_m$

参数怎么估计

前面知道$Y_i$ 服从Bernouli分布，既然分布已知了，我们自然会想到用极大似然估计的方法去估计参数，此时的似然函数是
$$L(\beta )=f(y_1,y_2,..,y_n)=\prod _{j=1}^n{p}_i^{y_j}(1-p_i{)}^{1-y_i}=\prod _{j=1}^n(\frac{p_i}{1-p_i}{)}^{y_i}(1-p_i)$$
其中$p_i=P(Y_i=1)=\frac{1}{1+e^{-x_i\beta }}$，又发现这样的关系$Log\frac{p_i}{1-p_i}=x_i\beta$，为了之后计算方便，先对上式两边取对数得到

$$LogL(\beta )=Logf(y_1,y_2,..,y_n)=\sum _{j=1}^n{y}_j(Log{p}_i)+(1-y_j)(Log(1-p_i))\text{\hspace{1em}(1)}$$$$=\sum _{j=1}^n{y}_{j}Log\frac{p_i}{1-p_i}+Log(1-p_i)=\sum _{j=1}^n{y}_j{x}_i\beta -Log(1+e^{x_i\beta })\text{\hspace{1em}(2)}$$
最大化这个似然函数，并取此时满足情况的$\beta$作为参数的估计值$\beta$，就能得到预测模型$E(Y_i)=P(Y_i=1)=\frac{1}{1+e^{-x_i\beta }}$了，而为什么要最大化这个似然函数呢，也就是极大似然估计的意义在哪？

• 因为我们的假设是$Y_i$独立同分布，这里的似然函数实质就是$Y_i(i=1,2,...,n)$的联合密度函数，当联合密度函数最大的时候，也就是概率最大的时候，事件最可能发生的时候，所以我们会想去最大化似然函数。

我想大部分读者都是对机器学习感兴趣来的，那这我们用一个机器学习里的名词，代价函数(Cost function)，来进行接下来的步骤，把(1)式做个小小修改就变成了，大家熟悉的代价函数

$$Cost(\beta )=-\frac{1}{n}\sum _{j=1}^n{y}_j(Log{p}_i)+(1-y_j)(Log(1-p_i))\text{\hspace{1em}(3)}$$

其实质就是将似然函数的对数函数做了一个平均，最大化似然函数的对数函数，也就是最小化这个代价函数

如果想要更严格地估计，我们还可以在这个基础上，再添加惩罚项(Penalty)，这个步骤也叫正则化(Regularization)，常见的惩罚项是一范数和二范数，也分别叫做Lasso和Ridge，叫啥都无所谓，实质都是数学。

$$\begin{gathered} Cos{t}_{L_1}(\beta )=Cost(\beta )+\frac{\lambda }{n}\sum _{j=1}^m|{\beta }_j| \\ Cos{t}_{L_2}(\beta )=Cost(\beta )+\frac{\lambda }{2n}\sum _{j=1}^m{\beta }_j^2 \end{gathered}$$

明白了这层关系后，进一步的问题就在于如何最小化代价函数，并且得到其对应的参数$\beta$

求参数$\beta$的方法常用的有两个，一个是梯度下降(Gradient descent)，另一个是牛顿迭代(Newton’s Iteration)。

梯度下降

对(3)式里的代价函数求导，而(3)式就是把(2)式做了一个变换$-\frac{(2)}{n}$，因此

$$\frac{\partial Cost(\beta )}{\partial \beta }=-\frac{1}{n}\frac{\partial (2)}{\partial \beta }=-\frac{1}{n}\sum _{j=1}^n{x}_i(y_j-p_i)$$

和之前一样，这里$p_i=P(Y_i=1)=\frac{1}{1+e^{-x_i\beta }}$

$x_i$和$y_j$都是已知，给定初值${\beta }^{(0)}=[{\beta }_0^{(0)},{\beta }_1^{(0)},{\beta }_2^{(0)},...,{\beta }_m^{(0)}{]}^{\prime }$后，得到$p_i^{(0)}$，因此参数${\beta }_m^{(0)}$的更新可以写成
$$\begin{gathered} {\beta }_m^{(t)}={\beta }_m^{(t-1)}-l\cdot \frac{\partial Cost({\beta }^{(t-1)})}{\partial {\beta }^{(t-1)}} \\ ={\beta }_m^{(t-1)}-l\cdot \frac{1}{n}\sum _{j=1}^n{x}_i(y_j-p_i^{(t-1)})\text{\hspace{1em}(4)} \end{gathered}$$
写成矩阵的形式
$${\beta }^{(t)}={\beta }^{(t-1)}-l\cdot \frac{1}{n}\cdot X^T\cdot (y-p)$$
其中$l$是学习速度(learning rate)，$X$是nx(m+1)的矩阵，$y$是nx1的向量，$p$是nx1的向量($p=[p_1,p_2,...,p_n{]}^{\prime }$)，在实际的操作中，我们会多次取不同的初值，由此希望达到全局最小值。

以下是梯度下降的简单实现，其中省略了计算$p$的函数

def update_bata(X, y, beta, l):
	'''
	X: 自变量是一个(n,m+1)的矩阵
	y: 因变量是一个(n,1)的向量
	beta: 参数β是一个(m+1,1)的向量
	l: 学习速率
	'''
    n = len(y)

    #1 由(4)的算式得到p，设函数名为cal_p
    p= cal_p(X, beta)

    #2 (4)的一部分
    gradient = np.dot(X.T,  y-p)

    #3 Take the average cost derivative for each feature
    gradient /= N

    #4 - Multiply the gradient by our learning rate
    gradient *= l

    #5 - Subtract from our weights to minimize cost
    beta -= gradient

    return beta

牛顿迭代

可以说这个方法是从泰勒展开得到的灵感，$f(x)$在$x_k$处的展开式$f(x)=f(x_k)+f^{\prime }(x_k)(x-x_k)+\frac{1}{2!}{f}^{\prime \prime }(x_k)(x-x_k{)}^2+...$，我们想寻找满足$f(x)=0$的$x$，即牛顿迭代的终点是$f(x)$收敛到0

在这我们只取前两项，$h(x)=f(x_k)+f^{\prime }(x_k)(x-x_k)$，我们认为$h(x)$是$f(x)$的一个近似，那么有$f(x)=h(x)=0$，得到
$$x=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$$
进而有迭代
$$x_{k+1}=x_k-\frac{f(x_k)}{f^{\prime }(x_k)}$$
在我们的二元逻辑回归中，代价函数就是这里的$f(x)$，参数$\beta$更新方法是
$${\beta }^{(k)}={\beta }^{(k-1)}-\frac{cost({\beta }^{(k-1)})}{cos{t}^{\prime }({\beta }^{(k-1)})}$$
直至代价函数趋近于0。这里做一个区分，梯度下降方法中的代价函数不一定趋近于0。

---

---

以上就是全部内容了，笔者从统计的角度大致解释了下机器学习中逻辑回归损失函数的来源，希望能帮助到各位读者