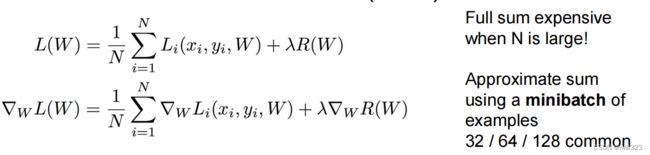2022CS231n笔记-正则化和优化算法

代码部分：全连接层网络_iwill323的博客-CSDN博客

目录

正则化

问题引出

 正则化作用

 L1和L2正则化

优化算法

随机梯度下降Stochastic Gradient Descent (SGD)

存在的问题

 SGD + Momentum

 原理

参数处理

pytorch中的SGD + Momentum

 Nesterov Momentum

原理

 评价

Adagrad 

原理

优缺点

RMSprop

pytorch中的RMSprop

Adam  

公式

偏移矫正版本

学习率调优

不同学习率的影响

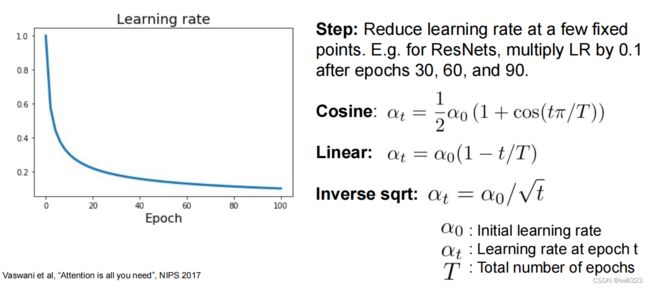
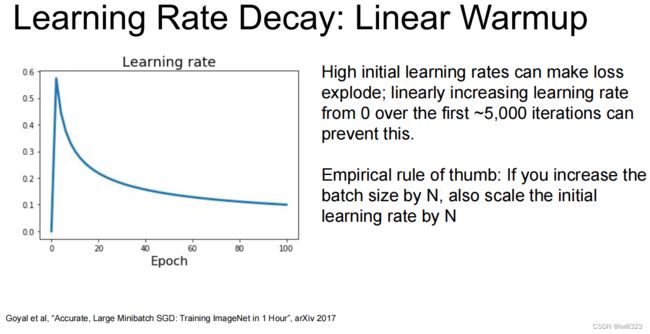
 学习率衰减方法

 使用建议

---

正则化

问题引出

How do we choose between W and 2W? 

 正则化作用

在损失函数中额外引入了正则项，用于对权重的调整，在最小化loss的同时，权重值的选择被限定了。比如，在W和2W之间，显然是选择了W

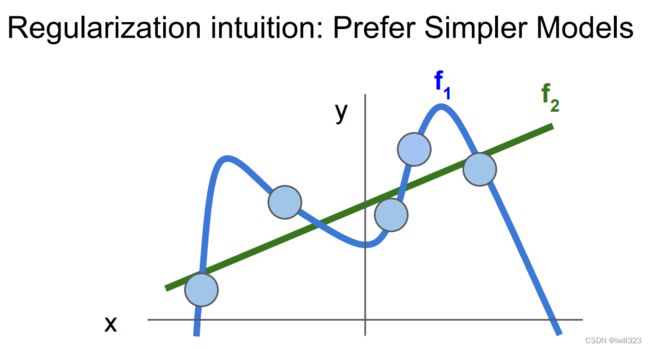
 加入了正则化项后，要想最小化loss，那么权重W也要尽可能的小，于是一些冗余的权重被抑制（比如高此项，参照下图），模型变得简单，防止过拟合

正则化的作用：

- Express preferences over weights

- Push against fitting the data too well so we don’t fit noise in the data

- Improve optimization by adding curvature

 L1和L2正则化

L2正则化倾向得到小而分散的权重，最终结果能考虑到各种输入的影响（如w2），而不是少数输入的影响（如w1），提高了模型的泛化能力，减弱过拟合

L1正则化倾向得到稀疏的权重（类似于w1）

优化

http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/演示网站

随机梯度下降Stochastic Gradient Descent (SGD)

现在一般使用minibatch

# Vanilla update
x+=-learning_rate*dx

存在的问题

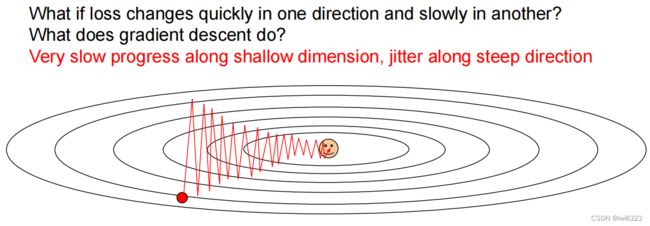
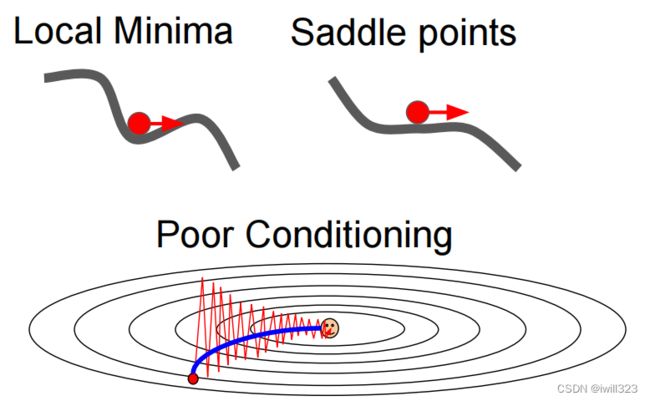
1.不同维度变化率差别大的时候，下降慢

在下图中，变量梯度并不指向最小值，输出对x方向输入变化不敏感，对y方向敏感，于是SGD算法在y方向会强烈振动，而在x方向进展缓慢

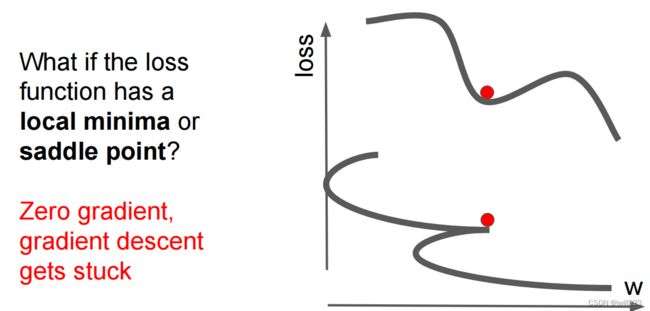
 2.可能会陷于局部最优点（低维）或在鞍点计算进展缓慢（高维）

3.由于使用了minibatch，在计算过程加入了噪声，走了弯路，慢

 SGD + Momentum

计算过程大大加快： With Momentum update, the parameter vector will build up velocity in any direction that has consistent gradient.

 原理

参考吴恩达的深度学习课程，我是这么理解：vt的初始值是0，所以vt其实就是计算过程中得到的历史梯度的叠加。并且考虑到，不同维度（方向）上梯度的计算是互不干涉的。参考上图，y方向的梯度振动很大，叠加的过程中相当一部分被抵消掉了，于是y方向的增量不大，起码不会像以前那样振动；x方向上的梯度一直是往右的，新算出来的x方向的梯度要加上原来计算出来的梯度，于是叠加起到了x方向上加速变化的作用，就像加速度之于速度（这也是将算法命名为Momentum动量的原因）。最终得到了蓝色线那样的优化过程。

对于上面说的的鞍点和局部最小值问题，由于动量（过往dx）的影响，x能冲过这两个陷阱

参数处理

Here we see an introduction of a v variable that is initialized at zero, and an additional hyperparameter (mu) (its typical value is about 0.9). When cross-validated, this parameter is usually set to values such as [0.5, 0.9, 0.95, 0.99]. Optimization can sometimes benefit a little from momentum schedules, where the momentum is increased in later stages of learning. A typical setting is to start with momentum of about 0.5 and anneal it to 0.99 or so over multiple epochs.

出自官网CS231n Convolutional Neural Networks for Visual Recognition

pytorch中的SGD + Momentum

看上去和课件中写的计算方式一模一样

 Nesterov Momentum

原理

先介绍Momentum的另一种写法：

# Momentum update
v = mu * v - learning_rate * dx 
# integrate velocity
x += v # integrate position

 和正常的SGD相比，Momentum算法给x增加了一项mu*v，可以视作动量矫正。在使用SGD算法时，我们是利用x点的梯度对x点进行调整，那么Nesterov Momentum的思想是将从矫正后的点（x+mu*v）开始做梯度下降，这样与SGD算法达到了形式上的一致：

x_ahead = x + mu * v
# evaluate dx_ahead (the gradient at x_ahead instead of at x)
v = mu * v - learning_rate * dx_ahead
x += v

使用x_ahead = x + mu * v做变量替换

 评价

根据官网CS231n Convolutional Neural Networks for Visual Recognition：Nesterov Momentum enjoys stronger theoretical converge guarantees for convex functions and in practice it also consistenly works slightly better than standard momentum.也就是说Nesterov Momentum比标准的Momentum要更好用

Adagrad 

原理

# Assume the gradient dx and parameter vector x
cache += dx**2
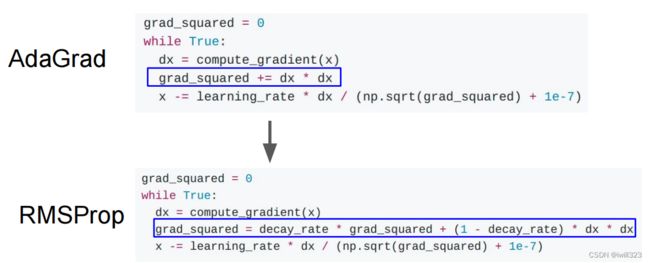
x += - learning_rate * dx / (np.sqrt(cache) + eps)

特点是，计算dx的时候，考虑过往计算梯度的历史。注意这里对dx采用的是取平方，这样过往振动大的方向上，新算出来的梯度要被大的数相除，学习率被自动调小了，更新更为谨慎；过往振动小或者几乎不怎么更新的方向上，学习率被自动调大了，学习加速。

优缺点

优点：可以消除梯度下降中的摆动，不会在振动大的方向上偏离。于是可以用一个更大学习率，加快算法学习速度。

缺点：A downside of Adagrad is that in case of Deep Learning, the monotonic learning rate usually proves too aggressive and stops learning too early. 学习率单调下降，算着算着变成了0，过早停止学习

RMSprop

Here, decay_rate is a hyperparameter and typical values are [0.9, 0.99, 0.999].  RMSProp still modulates the learning rate of each weight based on the magnitudes of its gradients, which has a beneficial equalizing effect, but unlike Adagrad the updates do not get monotonically smaller. 

pytorch中的RMSprop

Adam  

公式

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

和 RMSprop相比，就是把x更新式子中的dx变成了m而已。RMSProp和momentum的结合

推荐值：eps = 1e-8, beta1 = 0.9, beta2 = 0.999，learning_rate = 1e-3 or 5e-4

偏移矫正版本

之所以要矫正，是因为first moment和 second moment一开始的值接近0 。虽然在x的计算中，是小数m除以小数np.sqrt(v) ，但是搞不好这个结果非常大，就会影响到一开始的计算，所以采用偏移矫正，让m变大

# t is your iteration counter going from 1 to infinity
m = beta1*m + (1-beta1)*dx
mt = m / (1-beta1**t)
v = beta2*v + (1-beta2)*(dx**2)
vt = v / (1-beta2**t)
x += - learning_rate * mt / (np.sqrt(vt) + eps)

学习率调优

不同学习率的影响

学习率小了容易发散，大了得不到好的优化结果甚至发散，可以理解为最优值的调整只在毫厘之间，如果学习率大了，那么每次权重变化太大，每每“跨过”最优值

根据课程PPT，all of these are good learning rates. 我的理解是，选择高学习率和低学习率都是对的，也都是错的。什么阶段就做什么样的事情，学习率用在合适的阶段就是对的，用在不合适阶段就是错的。重在计算过程中对学习率的调整

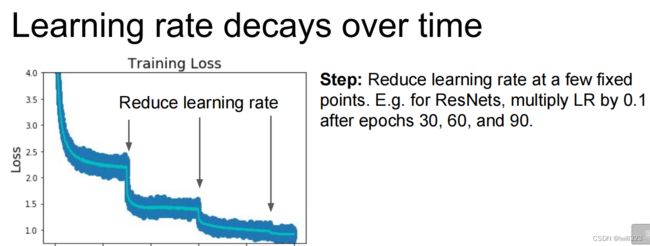
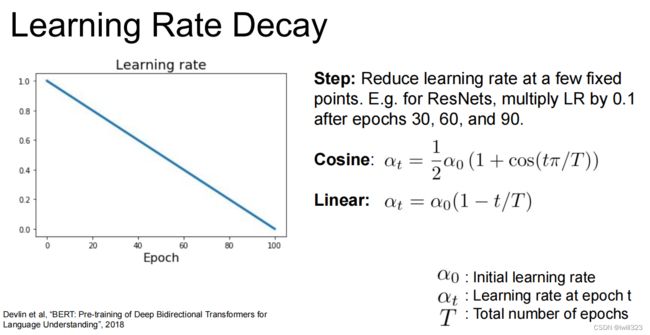
 学习率衰减方法

 

 

 

 使用建议

• Adam is a good default choice in many cases; it often works ok even with constant learning rate
• SGD+Momentum can outperform Adam but may require more tuning of LR and schedule
• If you can afford to do full batch updates then try out L-BFGS (and don’t forget to disable all sources of noise)

官方PPT网站Index of /slides/2022 希望引用图片没有侵权