python深度学习进阶（自然语言处理）—word2vec
python深度学习进阶（自然语言处理）—word2vec
摘要
- 基于推理的方法以预测为目标，同时获得了作为副产物的单词的分布式表示。
- word2vec 是基于推理的方法，由简单的 2 层神经网络构成。
- word2vec 有 skip-gram 和 CBOW 模型。
- CBOW 模型从多个单词（上下文）预测 1 个单词（目标词）。
- skip-gram 模型反过来从 1 个单词（目标词）预测多个单词（上下文）。
- 由于 word2vec 可以进行权重的增量学习，所以能够高效地更新或添加单词的分布式表示。
1. 基于推理的方法和神经网络
1.1 基于计数的方法的问题
基于计数的方法获得单词的分布式表示：使用整个语料库的统计数据（共现矩阵和 PPMI 等），通过一次处理（SVD 等）获得单词的分布式表示。
基于推理的方法获得单词的分布式表示：使用神经网络，通常在 mini-batch 数据上进行学习。
对于一个
的矩阵，SVD 的复杂度是
，这表示计算量与
的立方成比例增长。如此大的计算成本，即便是超级计算机也无法胜任。实际上，利用近似方法和稀疏矩阵的性质，可以在一定程度上提高处理速度，但还是需要大量的计算资源和时间。
在现实世界中，语料库处理的单词数量非常大。比如，英文的词汇量多达 100w+。如此之大的词汇量，如果使用基于计数的方法就需要生成一个 100w * 100w 的庞大矩阵，对如此庞大的矩阵执行 SVD 显然是不现实的。
基于计数的方法和基于推理的方法的比较：
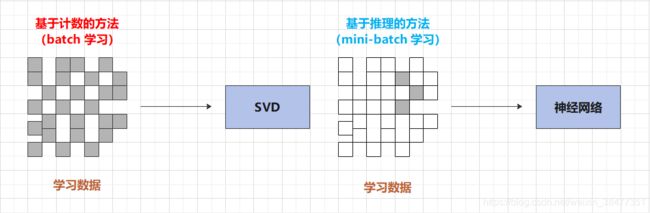图 3-1 基于计数的方法和基于推理的方法的比较
（1）基于计数的方法一次性处理全部学习数据；基于推理的方法使用部分学习数据逐步学习。
（2）神经网络的学习可以使用多台机器、多个 GPU 并行执行，从而加速整个学习过程。
1.2 基于推理的方法的概要
基于推理的方法的主要操作是 “推理”。如图 3-2 所示，当给出周围的单词（上下文）时，预测 “?” 处会出现什么单词，这就是推理。
图 3-2 基于两边的单词（上下文），预测 “?” 处出现什么单词
解开图 3-2 中的推理问题并学习规律，就是基于推理的方法的主要任务。通过反复求解这些推理问题，可以学习到单词的出现模式。从 “模式视角” 出发，这个推理问题如图 3-3 所示。
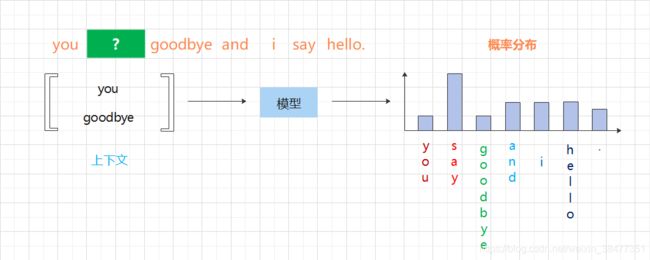图 3-3 基于推理的方法：输入上下文，模型输出各个单词的出现概率
基于推理的方法的全貌：使用语料库来学习模型，使之能做出正确的预测。另外，作为模型学习的产物，我们得到了单词的分布式表示。
（1）引入某种模型，将神经网络用于此模型；
（2）模型接收上下文信息作为输入，并输出（可能出现的）各个单词的出现概率。
1.3 神经网络中单词的处理方法
将单词表示为文本、单词ID和 one-hot 表示：
图 3-4 单词、单词 ID 以及它们的 one-hot 表示
要将单词转化为 one-hot 表示，就需要准备元素个数与词汇个数相等的向量，并将单词 ID 对应的元素设为 1，其他元素设为 0。像这样，只要将单词转化为固定长度的向量，神经网络的输入层的神经元个数就可以固定下来（图 3-5）。
图 3-5 输入层的神经元：各个神经元对应于各个单词。图中神经元为 1 的地方用蓝色绘制，为 0 的地方用白色绘制
如图 3-5 所示，输入层由 7 个神经元表示，分别对应于 7 个单词（第 1 个神经元对应于 you，第 2 个神经元对应于 say）。
基于神经网络的全连接层的变换：
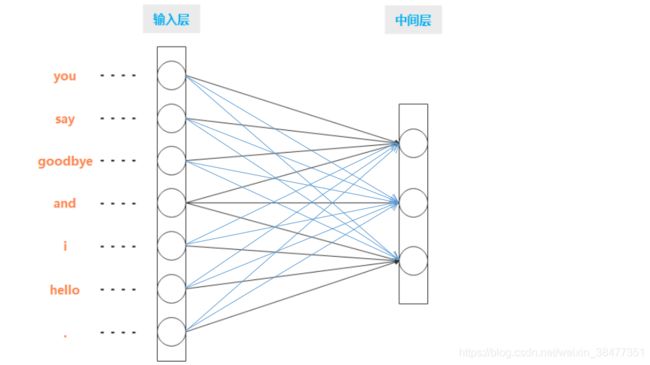图 3-6 基于神经网络的全连接层的变换：输入层的各个神经元分别对应于 7 个单词（中间层的神经元暂为3个）
如图 3-6 所示，全连接层通过箭头连接所有节点。这些箭头拥有权重（参数），它们和输入层神经元的加权和成为中间层的神经元。
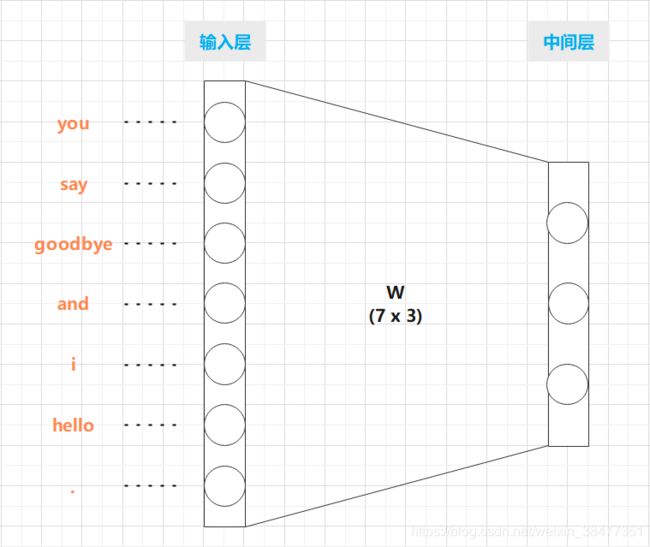图 3-7 基于全连接层的变换的简化图示：将全连接层的权重表示为一个 7 x 3 形状的 W 矩阵
Python 代码实现基于神经网络的全连接层的变换：
import numpy as np
class MatMul:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x):
W, = self.params
out = np.dot(x, W)
self.x = x
return out
def backward(self, dout):
W, = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
self.grads[0][...] = dW
return dx"""基于神经网络全连接层的变换"""
import sys
sys.path.append("..")
import numpy as np
from common.layers import MatMul
C = np.array([[1, 0, 0, 0, 0, 0, 0]]) # 输入
W = np.random.randn(7, 3) # 权重
# 方案一
h = np.dot(C, W) # 中间节点
print(h)
# 方案二
layer = MatMul(W)
h = layer.forward(C) # 中间节点
print(h)
[[-0.00183343 -0.41558399 0.13295223]]
[[-0.00183343 -0.41558399 0.13295223]]矩阵 C：one-hot 表示，单词 ID 对应的元素是 1，其他地方都是 0。
上述代码的 C 和 W 的矩阵乘积相当于 “提取” 权重的对应行向量。
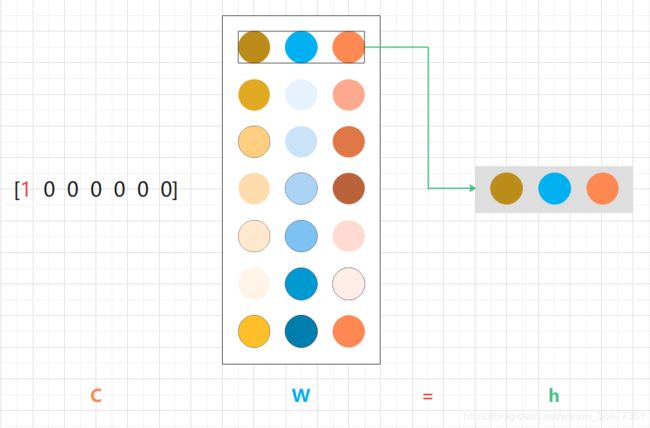图 3-8 在上下文 C 和权重 W 的矩阵乘积中，对应位置的行向量被提取
2. 简单的 word2vec
2.1 CBOW 模型的推理
continuous bag-of-words（CBOW）模型：根据上下文预测目标词的神经网络（“目标词” 是指中间的单词，它周围的单词是 “上下文”）。通过训练这个 CBOW 模型，使其尽可能地进行正确的预测，我们可以获得单词的分布式表示。
CBOW 模型的输入是上下文。这个上下文用 ["you", "goodbye"] 这样的单词列表表示。我们将其转换为 one-hot 表示，以便 CBOW 模型可以进行处理。在此基础上，CBOW 模型的神经网络可以画成图 3-9 这样。
从输入层到中间层神经元的变换由相同的全连接层（权重为 
）完成；从中间层到输出层神经元的变换由另一个全连接层（权重为 
）完成。
图 3-9 CBOW 模型的网络结构
输入层：2 个输入层。这里，因为我们对上下文仅考虑两个单词，所以输入层有 2 个。如果对上下文考虑 N 个单词，则输入层会有 N 个。
中间层：中间层的神经元是各个输入层经全连接层变换后得到的值的 “平均”。就上面的例子而言，经全连接层变换后，第 1 个输入层转化为 h1，第 2 个输入层转化为 h2，那么中间层的神经元是
。
输出层：输出层有 7 个神经元。这些神经元对应于各个单词。输出层的神经元是各个单词的得分（被解释为概率之前的值），它的值越大，说明对应单词出现的概率（对得分应用 Softmax 函数，得到概率）就越高。
权重的各行对应各个单词的分布式表示：
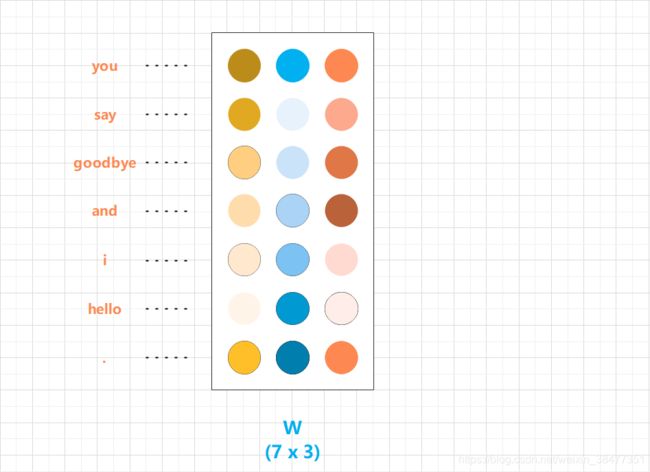图 3-10 权重的各行对应各个单词的分布式表示
如图 3-10 所示，权重
中间层的神经元数量比输入层少。
中间层需要将预测单词所需的信息压缩保存，从而产生密集的向量表示。这时，中间层被写入了我们人类无法解读的代码，这相当于 “编码” 工作。而从中间层的信息获得期望结果的过程则称为 “解码”。这一过程将被编码的信息复原为我们可以理解的形式。
层视角下的 CBOW 模型的网络结构：
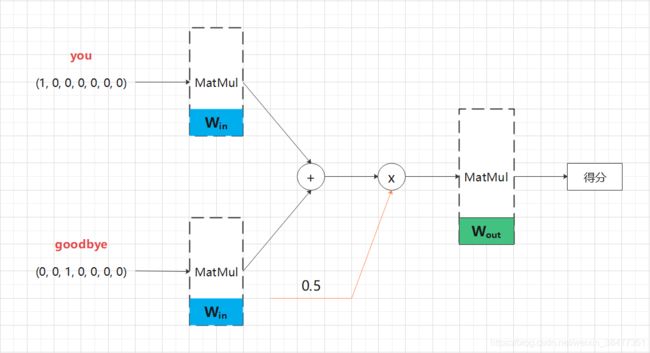图 3-11 层视角下的 CBOW 模型的网络结构
（1）CBOW 模型一开始有两个 MatMul 层，这两个层的输出被加在一起；
（2）对这个相加后得到的值乘以 0.5 求平均，可以得到中间层的神经元；
（3）将另一个 MatMul 层应用于中间层的神经元，输出得分。
Python 实现 CBOW 模型的推理：
"""CBOW 模型的推理"""
import sys
import numpy as np
sys.path.append("..")
from common.layers import MatMul
# 样本的上下文数据
c0 = np.array([[1, 0, 0, 0, 0, 0, 0]])
c1 = np.array([[0, 0, 1, 0, 0, 0, 0]])
# 权重的初始值
W_in = np.random.randn(7, 3)
W_out = np.random.randn(3, 7)
# 生成层
in_layer0 = MatMul(W_in)
in_layer1 = MatMul(W_in)
out_layer = MatMul(W_out)
# 正向传播
h0 = in_layer0.forward(c0)
h1 = in_layer1.forward(c1)
h = 0.5 * (h0 + h1)
s = out_layer.forward(h)
print(s)
[[ 0.20642852 -0.04648919 0.1134865 -0.34961565 -0.46868242 0.68511301 -0.04560098]]2.2 CBOW 模型的学习
CBOW 模型只是学习语料库中单词的出现模式。如果语料库不一样，学习到的单词的分布式表示也不一样。比如，只使用 “体育” 相关的文章得到的单词的分布式表示，和只使用 “音乐” 相关的文章得到的单词的分布式表示将有很大不同。
学习过程：
(1) 使用 Softmax 函数将得分转化为概率；
(2) 求这些概率和监督标签之间的交叉熵误差，并将其作为损失进行学习。
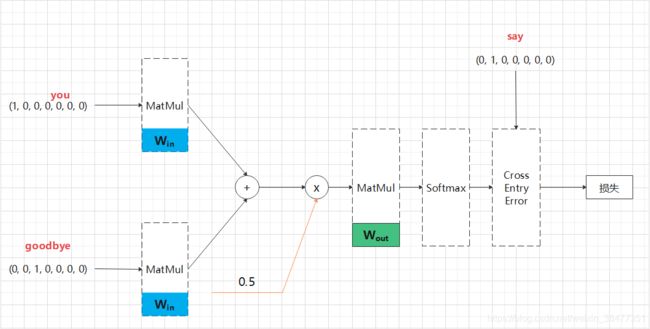图 3-12 学习时的 CBOW 模型的神经网络
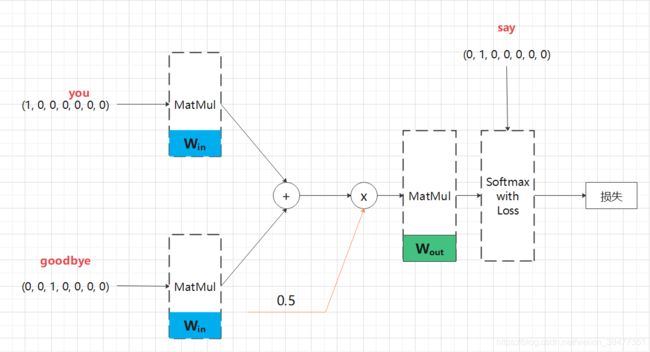图 3-13 将 Softmax 层和 Cross Entropy Error 层统一为 Softmax with Loss 层的学习时的 CBOW 模型的神经网络
2.3 word2vec 的权重和分布式表示
输入侧和输出侧的权重都可以被视为单词的分布式表示：
(1) 输入侧的全连接层的权重
(2) 输出侧的全连接层的权重
最终应该使用哪个权重作为单词的分布式表示呢？
A. 只使用输入侧的权重（word2vec 中，最受欢迎）
B. 只使用输出侧的权重
C. 同时使用两个权重值
在采用方案 C 的情况下，根据如何组合这两个权重，存在多种方式，其中一个方式就是简单地将这两个权重相加。
3. 学习数据的准备
3.1 上下文的目标词
word2vec 中使用的神经网络的输入是上下文，它的正确解标签是被这些上下文包围在中间的单词，即目标词。也就是说，我们要做的事情是，当向神经网络输入上下文时，使目标词出现的概率高（为了达成这一目标而进行学习）。