查找——二叉排序树Binary Sorting Tree的详解与实现
查找
- 8.4 二叉排序树
-
- 8.4.1 二叉排序树的定义
- 8.4.2 二叉排序树的实现
-
- 二叉排序树类模板
- 二叉排序树具体函数
-
- 查找
- 插入
- 删除
- 判定树是否是二叉排序树
- 8.4.3 效率分析
8.4 二叉排序树
为了适应动态查找,宜将数据组织表组织成树表。二叉排序树是一种基于二叉树的动态查找结构。
8.4.1 二叉排序树的定义
- 二叉排序树或是一棵空树,或者是具有下列性质的二叉树:
1)左子树(如果存在)上所有结点的关键字都小于根结点的关键字。
2)右子树(如果存在)上所有结点的关键字都大于根结点的关键字。
3)左子树和右子树也是二义排序树。 - 任意结点的关键字大于它的左子树上所有结点的关键字,同时小于它的右子树上所有结点的关键字。
- 如果对一棵二叉排序树进行中序遍历,得到的结点序列是按关键字从小到大的顺序序列。

8.4.2 二叉排序树的实现
二叉排序树类模板
- 树的结点结构
template<class ElemType> class BSTNode
{
public:
ElemType key;
BSTNode *left,*right;
BSTNode(ElemType value,BSTNode *l=NULL,BSTNode *r=NULL)
{
key=value;
left=l;
right=r;
}
};
- 树的类模板定义
#include "BinTreeNode.h"
#include 二叉排序树具体函数
查找
在二叉排序树上进行查找的过程,是从根结点开始,沿某一个分支逐层向下进行比较判等的过程。设要在二叉排序树中查找关键字为key的结点,查找过程从根结点开始,如果根指针为NULL,则查找不成功;否则用给定值kcy与根结点的关键字进比较。如果给定值等于根结点的关键字,则查找成功,返回查找成功信息,并报告战到的结点地址;如果给定值key小于根结点的关键字,则在根结点的左子树上递流找;否则,在根结点的右子树上递归查找。为了便于在二义排序树上插入结点。算法在实现时还返回了相应的双亲结点的指针,下面给出二叉排序树查找的迭代算法的C+实现。
template<class ElemType> BinTreeNode<ElemType>*
BinSortTree<ElemType>::Find(const ElemType &key,BinTreeNode<ElemType> *&f)const
{
BinTreeNode<ElemType> *p=root;
f=NULL;
while(p!=NULL && p->data!=key)
{
if(key<p->data)
{
f=p;
p=p->left;
}
else
{
f=p;
f=f->right;
}
}
return p;
}
插入
- 为了向二叉排序树插入一个新元素,必须先检查这个元素在二又排序树中是否已经存在。因此,在插入之前,首先在二叉排序树中检查待插入的数据元素,如果查找成功,说明树中已经存在这个数据元素,则不再插入;如果查找不成功,说明树中不存在关键字等于给定值的数据元素,则把新元素插到查找操作失败的地方。
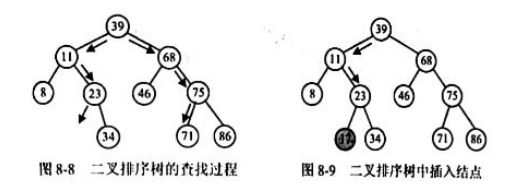
- 例如,图8-8所示的二叉排序树中插入关键字为17的新元素。首先在二叉排序树中查找关键字等于给定值17的数据元素是否存在,查找操作返回值为NULL,查找失败,可以插入。由于是从关键字为23的结点中又向左子树方向查找时查找指针变空的,因此把新元素作为关键字为23的结点的左孩子插入二叉排序树中,插入结果如图8-9所示。
template<class ElemType> bool BinSortTree<ElemType>::Insert(const ElemType e)
{
cout<<"insert "<<e;
BinTreeNode<ElemType> *f;//指向被查找结点的双亲
if(Find(e,f)==NULL)//查找失败,插入成功
{
BinTreeNode<ElemType> *p;//插入的新结点
p=new BinTreeNode<ElemType>(e);
if(IsEmpty())//空二叉树,新结点为根节点
root=p;
else if(e<f->data)//e小于其双亲,插入节点为f的左孩子
f->left=p;
else
f->right=p;
return true;
}
else//查找成功,插入失败
return false;
}
- 利用二叉排序树的插入算法,可以很方便地建立二叉排序树。
例如,有一个关键字的输入序列为{39,11,68,46,75,23,7,8,86,34}的数据元素序列。从空的二叉子树开始,逐一插入这些结点,从而建立起最终的二叉排序树。
插入过程如图8-10所示显然,每次插入一个数据元素,都要从根结点出发查找到插入位置,然后把新元素为叶子插入二叉排序树中,因此,不需移动数据元素,只需修改相应结点中的一个空着计即可。
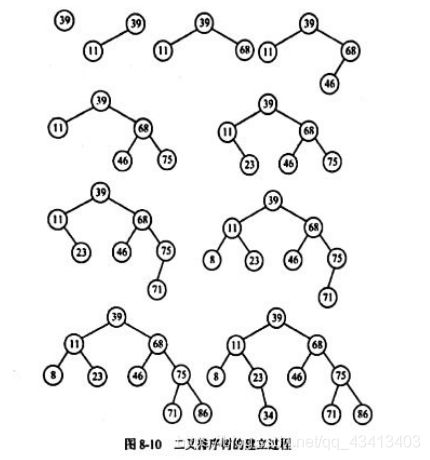
- 对于同样一组数据元素,由于输入顺序不同,建立起来的二叉排序树的形态也不同。例如,有三个数据元素{39,11,68},图8-11中的二叉排序树(a)、(b)、(c)、(d),(e)分别是由输入序列:{68,11,39},{68,39,11},{39,11,68},{11,68,39},{11,39,68}得到的。显然,这些二叉排序树的查找性能是不一样的。由此可见,如果输入序列选得不好,会建立起一棵单支树,使得二叉排序树查找性能和顺序查找一样。

删除
- 在二叉排序树中删除一个数据元素时,必须将因删除元素而断开的二叉链表重新链接起来,同时确保不会失去二叉排序树的性质。此外,为了保证在执行删除后二又排序树的查找性能不降低,还需要做到重新链接后二又排序树的高度不增加。所有这些因素都应当在删除算法中得到体现。
- 在二叉排序树中删除一个数据元素的算法思想如下:
(1)如果被删除的数据元素是叶子,则只需将其双亲指向它的指针置空,再释放该数据元素的存储空间即可;
(2)如果被删除的数据元素只有左子树而没有右子树,则可以拿它的左孩子顶替它的位置,再释放该数据元素的存储空间即可;如果被删除的数据元素只有右子树而没有左子树,可以拿它的右核子顶替它的位置,再释放该数据元素的存储空间即可;
(3)如果被删除的数据元素左、右子树都存在,则有四种处理方法:
其一,可以在它的左子树中寻找关键字值最大的数据元素(其左子树中序遍历中最后一个被访问的数据元素)x,用x的值代替被删除数据元素的、再来删除数据元素x(x一定没有右子树)。例如,在图8-12中想要删除关键字为y的数据元素,它有左、右子树,在它的左子树中找中序遍历时第一个被访问的数据元素为关键字等于34,用它的值代替被删除数据元素的值,接下来再删除关键字为34的据元素,该数据元素没有左、右子树,可直接删除。
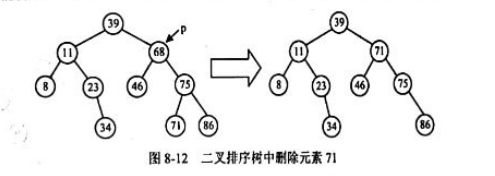
其二,可以在它的右子树中寻找慧字值最小的数据元素(其右子树中序遍历中第一个被访问的数据元素)x用x的值代酱被删除数据元素的值,再来删除数据元素x(x没有左子树)。例如,在图8-12中想别除关键字为68的数据元素,它有左、右子树,在它的右子树中找中序遍历时第一个访问的数据元素为关键字等于71,用它的值代替被删除数据元素的值,接下来再删除关键字为71的数据元素,元素71没有左、右子树,可直接删除。
其三,可以先把它的右子树作为左子树中关键字值最大的数据元素x的右子树,然后再删除结点。其四,可以先把它的左子树作为右子树中关键字值最小的数据元素x的左子树,然后再删除结点。
后两种法可能会增加二叉排序树的高度,(数的查找与高度相关,高度大,搜索的效率低)。第二种方法和第一种方法类似。
template<class ElemType> void
BinSortTree<ElemType>::Delete(BinTreeNode<ElemType> *&p)
{
BinTreeNode<ElemType> *tmpPtr,*tmpF;
if(p->left==NULL && p->right==NULL)//p为叶结点
{
delete p;
p=NULL;
}
else if(p->left==NULL)//p的左子树为空
{
tmpPtr=p;
p=p->right;
delete tmpPtr;
}
else if(p->right==NULL)//p的右子树为空
{
tmpPtr=p;
p=p->left;
delete tmpPtr;
}
else//p的左右子树都存在
{
tmpF=p;
tmpPtr=p->left;
while(tmpPtr->right!=NULL)
{
//查找p在中序序列中直接前驱tmpPtr及其双亲tmpF
tmpF=tmpPtr;
tmpPtr=tmpPtr->right;
}
p->data=tmpPtr->data;//将tmpPtr指向结点的数据元素值赋值给被删除结点
if(tmpF->right==tmpPtr)//删除tmpPtr的结点
Delete(tmpF->right);
else
Delete(tmpF->left);
}
}
判定树是否是二叉排序树
template<class ElemType> bool BinaryTree<ElemType>::IsBinSortTree(BinTreeNode<ElemType> *p)
{
if(p==NULL)
return true;
else if(p->left==NULL && p->right==NULL)
return true;
else if(p->left==NULL && p->right!=NULL && p->right->data > p->data)
return IsBinSortTree(p->right);
else if(p->left!=NULL && p->left->data < p->data &&p->right==NULL)
return IsBinSortTree(p->left);
else if(p->left->data < p->data && p->right->data > p->data)
return IsBinSortTree(p->left)&&IsBinSortTree(p->right);
else
return false;
}
8.4.3 效率分析
- 在二叉排序树上的查找过程实际上走了一条从根到所查结点的路径,所需比较次数为该结点所在的层次数。因此,查找成功时,关键字的比较次数不超过树的高度。但是含有n个结点的二叉排序树不是唯一的,所以树的高度也不一定相同。例如,图8-13(a)和图8-13(b)是由一组相同的数据元素组成的二叉排序树,但一棵树的高度为3,而另一棵树的高度为5。
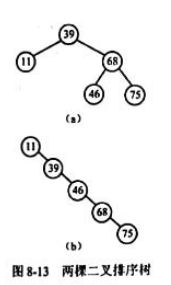
在图8-13(a)中查找75需要比较三次,而在图8-13(b)中查找75时,则需比较五次。
在等概率情况下,图8-13(a)所示二叉排序树的平均查找长度为(1+2+2+3+3)/5;而图8-13(b)所示二叉排序树的平均查找长度为(1+2+3+4+5)/5。 - 显然,当二叉排序树是完全二叉树时,其平均查找性能最佳为log2 n。与有序表的折半查找相同。当二叉排序树退化为一棵单支树时,二叉排序树的平均查找性能最差为(n+1)/2,与顺序表的平均查找长度相同。
最后, 代码工程压缩包