数学期望 极小值的几种求法
前言：
其中一维搜索方法这种思想，在图像二值化里面有应用。像二维码算法里面的条形码二值化，就是这种算法的进阶版。
缺点是只能按照一个方向进行搜索，且步伐需要调整。
目录：
- 数学期望例子
- 一维搜索方法求极值
- 黄金分隔法求极值
一 数学期望例子
普查某种疾病，为此要抽验N个人血，有两种方法：
方案1： 每个人分别去检验，这需要检验N次
方案2: k个人混合在一起检验，如果检验出来呈阳性，就全部检测一次，需要K+1一次，否则只检验一次。
假设每个人呈阳性概率为p,阴性概率为q(q=1-p).
求： 如果按照第二种方案，可以减少检验次数，且k取什么值最合适
解：
| X |  |
 |
 |
 |
- |
X的数学期望为
N个人平均化验次数为
则，只要选择合适的k,使得
， 二阶导数小于0，有极小值
"""
Created on Fri Oct 16 14:41:02 2020
@author: chengxf2
"""
import numpy as np
import matplotlib.pyplot as plt
def Draw():
q = 0.9
k = np.arange(2,20,1)
L =1-np.power(q,k)+1/k
plt.plot(k,L)
plt.show()
Draw()
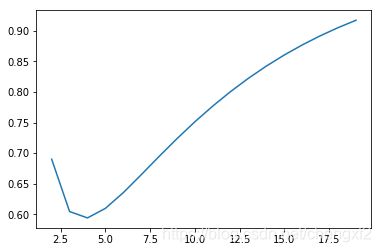
要取合适的k,使得L最小. ![k \in [2,N]](http://img.e-com-net.com/image/info8/ceb999582450413cb82118d5d2dc5178.gif){kind=small}
除了牛顿迭代法， 这里介绍两种方法，一维搜索区间法，黄金分割法，求解极小值
二 一维搜索的搜索区间
迭代公式：
其中：
: 当前点
: 下一个点
: 步长因子
: 当前搜索的步伐大小，以及方向
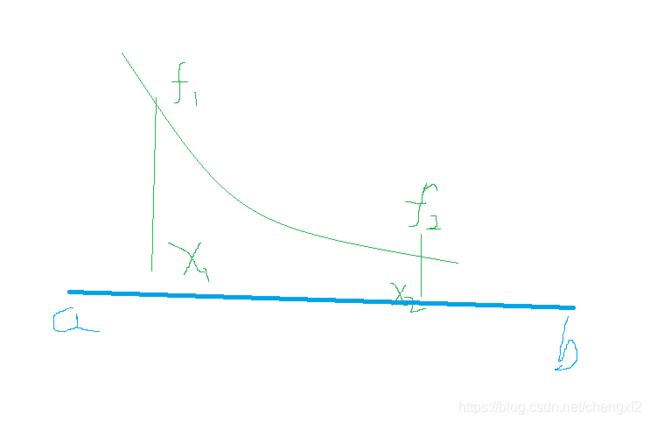
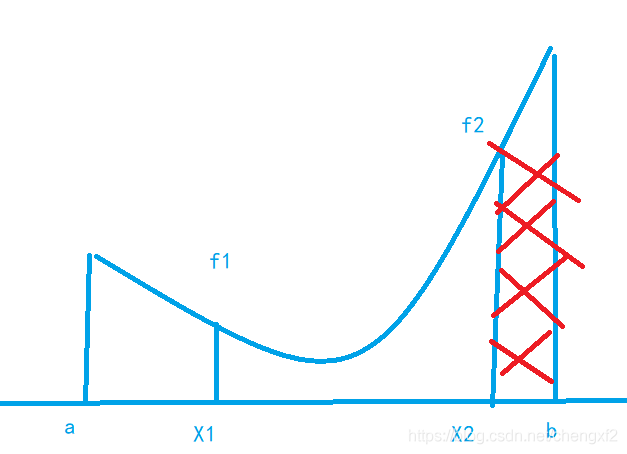
如上图，极小值点具有如下特征：
思想：
从一点出发，找到大，小 ，大特征的三个点，如果一个方向不成功，就反过来寻找
算法流程：
初始化：
,其中h 为步伐
if 
前进计算Forward
else(两点换位)
后退计算Backward
Forward( 前进计算）
if 
:
return [a, b] =[
]
else
h = 2h
return Forward
Backward( 反向计算）
;
if 
return ![[a,b]=[x_3,x_1]](http://img.e-com-net.com/image/info8/63b864e144214d9dbc4f1e930787a595.gif){kind=small}
else
return Backward
# -*- coding: utf-8 -*-
"""
Created on Wed Oct 21 15:32:43 2020
@author: chengxf2
"""
import numpy as np
class Find():
"""
计算f值
args
k
return
f
"""
def Calc(self,k):
#f= np.power(a,2)-7*a+10
q = 0.9
#k = np.arange(2,20,1)
f =1-np.power(q,k)+1/k
return f
def __init__(self):
self.h = 1.0 #搜索步伐
self.alpha = 1.0 #alpha
self.iterNum = 0
self.x0 = 2.0
"""
前进运算
args
x1: 左边点
x2: 中间点
a3: 右边点
"""
def Forward(self,x1,x2,f1,f2,h):
#print("\n Forward :",a1,a2,a3,f1,f2,f3,h)
self.iterNum = self.iterNum+1
x3 = x2+h*self.alpha
f3 = self.Calc(x3) #调到step1
if f2<=f3: #大 小 大 找到了
a = x1 #左边点
b = x2 #中间点
c = x3 #右边点
return a,b,c
else: #f2>f3 大 小 小
h = 2*h
x1 = x2 #这个点是大的
f1 = f2
x2 = x3
f2 =f3
return self.Forward(x1,x2,f1,f2,h) #再做前进运算
"""
反向运算
args
a1: 左边点
a2: 中间点
a3: 右边点
"""
def Backward(self,x1,x2,f1,f2,h):
#移动x1,x2 指针，保持x2为最小点位置
x3 = x2+h*self.alpha
f3 = self.Calc(x3)
if f3>=f2: #大 小 大 找到了
a = x1 #左边点
b = x2 #右边点
c = x3 #极小点
return a,b,c
else: #f3运算结果
=======一维搜索===
左区间 : 3.0 极小点 : 4.0 右区间 6.0 迭代次数 2
三 黄金分隔法
缺点： 当区间有全局极小值，但是多个极小值的时候，无法找到全局极小值
算法流程
始终落在极小值区间[a,b]的黄金分割点上
算法流程：
迭代 (step1)
终止
if 
跳转到step1
else
跳转到step1
# -*- coding: utf-8 -*-
"""
Created on Mon Oct 26 10:51:21 2020
@author: chengxf2
"""
import numpy as np
class Golden():
"""
一维函数
Args
f: 概率值
"""
def Calc(self,x):
q = 0.9
f =1-np.power(q,x)+1/x
return f
def __init__(self):
self.tol = 0.5 #精度要去
self.T = 0.618 #黄金分割系数
self.k = 1 #迭代次数
self.N = 100 #总人数
self.a = 0
self.b = 10
"""
迭代
args
a: 区间左
b: 区间右
"""
def Loop(self):
a = 2
b = self.N
for k in range(self.N):
x1 = a +(1.0-self.T)*(b-a) #x1
x2 = a +self.T*(b-a) #x2点
if (b-a)f2: #截取左边的 # 重新切换黄金分割点
a = x1
x1 = x2
x2 = x1+ self.T*(b-a)
else:
# print("\n 右边 截取 ")
b = x2 #截取右边的
x2 = x1
x1 = a + (1-self.T)*(b-a)
gd = Golden()
gd.Loop()