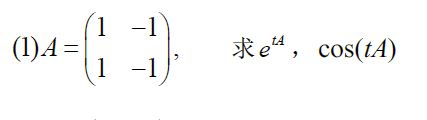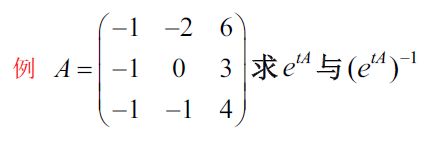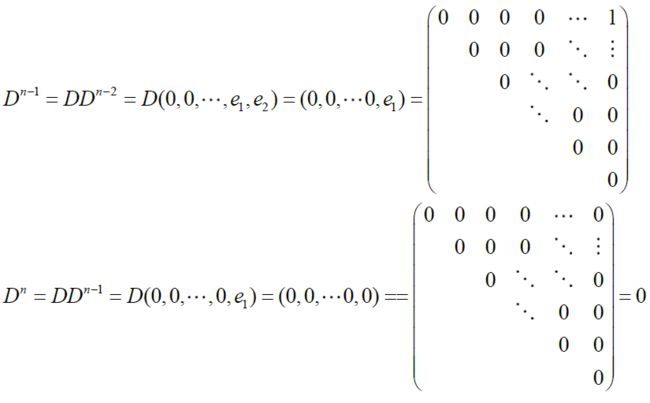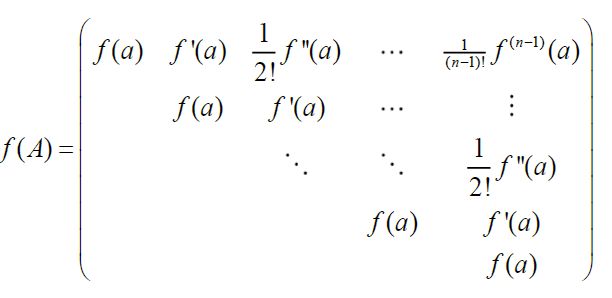【矩阵论】3. 矩阵运算与函数——矩阵函数的计算
10.4 谱公式计算矩阵函数
10.4.1 前置知识
a. 根遗传公式
设 n 阶 方 阵 A 特 根 λ ( A ) = { λ 1 , ⋯ , λ n } , 则 f ( A ) 的 特 根 为 λ ( f ( A ) ) = { f ( λ 1 ) , ⋯ , f ( λ n ) } 其 中 f ( x ) 为 任 意 多 项 式 函 数 , 满 足 f ( A ) = c 0 I + c 1 A + c 2 A 2 + ⋯ + c k A k \begin{aligned} &设n阶方阵A特根\lambda(A)=\{\lambda_1,\cdots,\lambda_n\} ,则f(A)的特根为\lambda(f(A))=\{f(\lambda_1),\cdots,f(\lambda_n)\}\\ &其中f(x)为任意多项式函数,满足f(A)=c_0I+c_1A+c_2A^2+\cdots+c_kA^k \end{aligned} 设n阶方阵A特根λ(A)={λ1,⋯,λn},则f(A)的特根为λ(f(A))={f(λ1),⋯,f(λn)}其中f(x)为任意多项式函数,满足f(A)=c0I+c1A+c2A2+⋯+ckAk
b. 0化式、特根与幂0阵
0化式:若多项式 f ( x ) f(x) f(x) 使 f ( A ) = 0 f(A)=0 f(A)=0 ,称 f ( x ) f(x) f(x) 为A的0化式
- A的全体特根是任意0化式 f ( x ) f(x) f(x) 的根 或 A的0化式 f ( x ) f(x) f(x) 含有A的全体不同根
- sp :若A为单阵,则0化式 f ( x ) f(x) f(x) 不含重复根,即不含大于2的幂次项
令 f ( x ) = ( x − 1 ) ( x − 2 ) 为 A 的 0 化 式 , 可 知 A 的 全 体 根 { 1 , 1 , 2 } 都 是 f ( x ) = ( x − 1 ) ( x − 2 ) 的 根 令f(x)=(x-1)(x-2)为A的0化式,可知A的全体根\{1,1,2\} 都是f(x)=(x-1)(x-2)的根 令f(x)=(x−1)(x−2)为A的0化式,可知A的全体根{1,1,2}都是f(x)=(x−1)(x−2)的根
若 A k = 0 ( k ≥ 2 ) A^k=0(k\ge 2) Ak=0(k≥2) 为幂0阵,则A的全体特根为 λ ( A ) = { 0 , ⋯ , 0 } \lambda(A)=\{0,\cdots,0\} λ(A)={0,⋯,0}
若 ( A − a I ) k = 0 ( k ≥ 2 ) (A-aI)^k=0(k\ge 2) (A−aI)k=0(k≥2) 为平移幂0阵,则A的全体根为 λ ( A ) = { a , ⋯ , a } \lambda(A)=\{a,\cdots,a\} λ(A)={a,⋯,a}
10.4.2 单阵谱公式
单 阵 A 有 谱 分 解 A = λ 1 G 1 + λ 2 G 2 + ⋯ + λ k G k , 且 f ( A ) = f ( λ 1 ) G 1 + ⋯ + f ( λ k ) G k 单阵A有谱分解A=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k,且f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k 单阵A有谱分解A=λ1G1+λ2G2+⋯+λkGk,且f(A)=f(λ1)G1+⋯+f(λk)Gk
10.4.3 广谱公式(非单阵2根2重)
若 A 满 足 ( A − a I ) 2 ( A − b I ) = 0 , 且 a ≠ b , 即 A 有 0 化 式 ( x − a ) 2 ( x − b ) , 则 有 广 谱 公 式 : f ( A ) = f ( a ) G 1 + f ( b ) G 2 + f ′ ( a ) D 1 , 其 中 G 1 + G 2 = I . D 1 为 固 定 矩 阵 \begin{aligned} &若A满足(A-aI)^2(A-bI)=0,且a\neq b,即A有0化式(x-a)^2(x-b),则有广谱公式:\\ &f(A)=f(a)G_1+f(b)G_2+f'(a)D_1,其中G_1+G_2=I.D_1为固定矩阵 \end{aligned} 若A满足(A−aI)2(A−bI)=0,且a=b,即A有0化式(x−a)2(x−b),则有广谱公式:f(A)=f(a)G1+f(b)G2+f′(a)D1,其中G1+G2=I.D1为固定矩阵
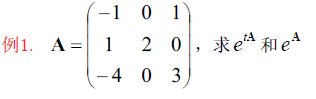
解 : ∣ A − λ A ∣ = ∣ − 1 − λ 0 1 1 2 − λ 0 − 4 0 3 − λ ∣ = ( λ − 1 ) 2 ( λ − 2 ) = 0 ⇒ λ ( A ) = { 1 , 1 , 2 } 由 于 ( A − I ) ( A − 2 I ) ≠ 0 , 0 化 式 有 重 根 , 所 以 A 不 是 单 阵 或 r ( A − I ) = r ( − 2 0 1 1 1 0 − 4 0 2 ) = 2 ≠ 3 − 2 = 1 , ∴ A 不 是 单 阵 ∵ ( A − I ) 2 ( A − I ) = 0 , ∴ 对 任 一 解 析 函 数 f ( x ) 有 广 谱 公 式 : f ( A ) = f ( 1 ) G 1 + f ( 2 ) G 2 + f ′ ( 1 ) D 1 取 不 同 的 多 项 式 求 G 1 , G 2 , D 1 ( 1 ) 令 f ( x ) = ( x − 1 ) ( x − 2 ) , f ′ ( x ) = ( x − 1 ) + ( x − 2 ) = 2 x − 3 , 有 f ( 1 ) = f ( 2 ) = 0 , f ′ ( 1 ) = − 1 代 入 公 式 后 得 , ( A − I ) ( A − 2 I ) = − D 1 ⇒ D 1 = − ( − 2 0 1 1 1 0 − 4 0 2 ) ( − 3 0 1 1 0 0 − 4 0 1 ) = ( − 2 0 1 2 0 − 1 − 4 0 2 ) ( 2 ) 令 f ( x ) = ( x − 1 ) 2 , f ( 1 ) = 0 , f ( 2 ) = 1 , f ′ ( x ) = 2 ( x − 1 ) , f ′ ( 1 ) = 0 ( A − I ) 2 = G 2 = ( 0 0 0 − 1 1 1 0 0 0 ) G 1 = I − G 2 = ( 1 0 0 1 0 − 1 0 0 1 ) ( 2 ) ′ 若 令 f ( x ) = ( x − 2 ) 2 , f ( 2 ) = f ′ ( 2 ) = 0 , f ( 1 ) = − 1 , 可 求 G 1 令 f ( x ) = e t x , f ′ ( x ) = t e t x , f ( A ) = e t A = f ( 1 ) G 1 + f ( 2 ) G 2 + f ′ ( 1 ) D 1 = e t G 1 + e 2 t G 2 + t e t D 1 即 e t A = e t ( 1 0 0 1 0 − 1 0 0 1 ) + e 2 t ( 0 0 0 − 1 1 1 0 0 0 ) + t e t ( − 2 0 1 2 0 − 1 − 4 0 2 ) = ( e t − 2 t e t 0 t e t e t − e 2 t + 2 t e t e 2 t e 2 t − e t − t e t − 4 t e t 0 e t + 2 t e t ) \begin{aligned} &解:\vert A-\lambda A\vert=\left | \begin{matrix} -1-\lambda & 0 &1\\1 & 2-\lambda &0\\-4&0&3-\lambda \end{matrix} \right |= (\lambda-1)^2(\lambda-2)=0\Rightarrow \lambda(A)=\{1,1,2\}\\ &由于(A-I)(A-2I)\neq 0,0化式有重根,所以A不是单阵\\ &或r(A-I)=r\left( \begin{matrix} -2&0&1\\1&1&0\\-4&0&2 \end{matrix} \right)=2\neq 3-2=1,\therefore A不是单阵\\ &\because (A-I)^2(A-I)=0,\therefore 对任一解析函数f(x)有广谱公式:\\ &f(A)=f(1)G_1+f(2)G_2+f'(1)D_1\\ &取不同的多项式求G_1,G_2,D_1\\ &\quad(1)令f(x)=(x-1)(x-2),f'(x)=(x-1)+(x-2)=2x-3,有f(1)=f(2)=0,f'(1)=-1\\ &\quad \quad代入公式后得,(A-I)(A-2I)=-D_1\Rightarrow D_1=-\left( \begin{matrix} -2&0&1\\1&1&0\\-4&0&2 \end{matrix} \right)\left( \begin{matrix} -3&0&1\\1&0&0\\-4&0&1 \end{matrix} \right)=\left( \begin{matrix} -2&0&1\\2&0&-1\\-4&0&2 \end{matrix} \right)\\ &\quad (2)令f(x)=(x-1)^2,f(1)=0,f(2)=1,f'(x)=2(x-1),f'(1)=0\\ &\quad \quad(A-I)^2=G_2=\left( \begin{matrix} 0&0&0\\-1&1&1\\0&0&0 \end{matrix} \right)\\ &\quad \quad G_1=I-G_2=\left( \begin{matrix} 1&0&0\\1&0&-1\\0&0&1 \end{matrix} \right)\\ &\quad (2)'若令f(x)=(x-2)^2,f(2)=f'(2)=0,f(1)=-1,可求G_1\\ &令f(x)=e^{tx},f'(x)=te^{tx},f(A)=e^{tA}=f(1)G_1+f(2)G_2+f'(1)D_1=e^tG_1+e^{2t}G_2+te^{t}D_1\\ &即e^{tA}=e^t\left( \begin{matrix} 1&0&0\\1&0&-1\\0&0&1 \end{matrix} \right)+e^{2t}\left( \begin{matrix} 0&0&0\\-1&1&1\\0&0&0 \end{matrix} \right)+te^t\left( \begin{matrix} -2&0&1\\2&0&-1\\-4&0&2 \end{matrix} \right)=\left( \begin{matrix} e^t-2te^t&0&te^t\\e^t-e^{2t}+2te^t&e^{2t}&e^{2t}-e^t-te^t\\-4te^t&0&e^t+2te^t \end{matrix} \right) \end{aligned} 解:∣A−λA∣=∣∣∣∣∣∣−1−λ1−402−λ0103−λ∣∣∣∣∣∣=(λ−1)2(λ−2)=0⇒λ(A)={1,1,2}由于(A−I)(A−2I)=0,0化式有重根,所以A不是单阵或r(A−I)=r⎝⎛−21−4010102⎠⎞=2=3−2=1,∴A不是单阵∵(A−I)2(A−I)=0,∴对任一解析函数f(x)有广谱公式:f(A)=f(1)G1+f(2)G2+f′(1)D1取不同的多项式求G1,G2,D1(1)令f(x)=(x−1)(x−2),f′(x)=(x−1)+(x−2)=2x−3,有f(1)=f(2)=0,f′(1)=−1代入公式后得,(A−I)(A−2I)=−D1⇒D1=−⎝⎛−21−4010102⎠⎞⎝⎛−31−4000101⎠⎞=⎝⎛−22−40001−12⎠⎞(2)令f(x)=(x−1)2,f(1)=0,f(2)=1,f′(x)=2(x−1),f′(1)=0(A−I)2=G2=⎝⎛0−10010010⎠⎞G1=I−G2=⎝⎛1100000−11⎠⎞(2)′若令f(x)=(x−2)2,f(2)=f′(2)=0,f(1)=−1,可求G1令f(x)=etx,f′(x)=tetx,f(A)=etA=f(1)G1+f(2)G2+f′(1)D1=etG1+e2tG2+tetD1即etA=et⎝⎛1100000−11⎠⎞+e2t⎝⎛0−10010010⎠⎞+tet⎝⎛−22−40001−12⎠⎞=⎝⎛et−2tetet−e2t+2tet−4tet0e2t0tete2t−et−tetet+2tet⎠⎞
λ ( A ) = { 1 , 1 , 2 } , 由 于 ( A − I ) ( A − 2 I ) ≠ 0 , ∴ A 不 是 单 阵 , ( A − I ) 2 ( A − 2 I ) = 0 有 广 谱 公 式 f ( A ) = f ( 1 ) G 1 + f ( 2 ) G 2 + f ′ ( 1 ) D 1 取 不 同 多 项 式 求 G 1 , G 2 , D 1 ( 1 ) 令 f ( x ) = ( x − 1 ) ( x − 2 ) , f ′ ( x ) = ( x − 1 ) + ( x − 2 ) , f ( 1 ) = f ( 2 ) = 0 , f ′ ( 1 ) = − 1 ( A − I ) ( A − 2 I ) = − D 1 ⇒ D 1 = − ( A − I ) ( A − 2 I ) = ( 0 1 0 0 0 0 0 0 0 ) ( 2 ) 令 f ( x ) = ( x − 1 ) 2 , f ( 1 ) = f ′ ( 1 ) = 0 , f ( 2 ) = 1 , 代 入 解 析 式 得 : ( A − I ) 2 = G 2 = ( 0 0 0 0 0 0 0 0 1 ) , G 1 = I − G 2 = ( 1 0 0 0 1 0 0 0 0 ) ∴ f ( A ) = f ( 1 ) G 1 + f ( 2 ) G 2 + f ′ ( 1 ) D 1 = f ( 1 ) ( 1 0 0 0 1 0 0 0 0 ) + f ( 2 ) ( 0 0 0 0 0 0 0 0 1 ) + f ′ ( 1 ) ( 0 1 0 0 0 0 0 0 0 ) f ( x ) = e t x , f ( 1 ) = e t , f ( 2 ) = e 2 t , f ′ ( 1 ) = t e t 可 得 e t A = ( e t t e t e t e 2 t ) \begin{aligned} &\lambda(A)=\{1,1,2\},由于(A-I)(A-2I)\neq 0,\therefore A不是单阵,(A-I)^2(A-2I)=0\\ &有广谱公式 f(A)=f(1)G_1+f(2)G_2+f'(1)D_1\\ &取不同多项式求G_1,G_2,D_1\\ & \quad (1)令f(x)=(x-1)(x-2),f'(x)=(x-1)+(x-2),f(1)=f(2)=0,f'(1)=-1\\ &\quad \quad (A-I)(A-2I)=-D_1\Rightarrow D_1=-(A-I)(A-2I)=\left( \begin{matrix} 0&1&0\\0&0&0\\0&0&0 \end{matrix} \right)\\ &\quad (2)令f(x)=(x-1)^2,f(1)=f'(1)=0,f(2)=1,代入解析式得:\\ &\quad \quad (A-I)^2=G_2=\left( \begin{matrix} 0&0&0\\0&0&0\\0&0&1 \end{matrix} \right),G_1=I-G_2=\left( \begin{matrix} 1&0&0\\0&1&0\\0&0&0 \end{matrix} \right)\\ &\therefore f(A)=f(1)G_1+f(2)G_2+f'(1)D_1=f(1)\left( \begin{matrix} 1&0&0\\0&1&0\\0&0&0 \end{matrix} \right)+f(2)\left( \begin{matrix} 0&0&0\\0&0&0\\0&0&1 \end{matrix} \right)+f'(1)\left( \begin{matrix} 0&1&0\\0&0&0\\0&0&0 \end{matrix} \right)\\ &f(x)=e^{tx},f(1)=e^t,f(2)=e^{2t},f'(1)=te^{t}\\ &可得e^{tA}=\left( \begin{matrix} e^t&te^t&\\&e^t&\\&&e^{2t} \end{matrix} \right) \end{aligned} λ(A)={1,1,2},由于(A−I)(A−2I)=0,∴A不是单阵,(A−I)2(A−2I)=0有广谱公式f(A)=f(1)G1+f(2)G2+f′(1)D1取不同多项式求G1,G2,D1(1)令f(x)=(x−1)(x−2),f′(x)=(x−1)+(x−2),f(1)=f(2)=0,f′(1)=−1(A−I)(A−2I)=−D1⇒D1=−(A−I)(A−2I)=⎝⎛000100000⎠⎞(2)令f(x)=(x−1)2,f(1)=f′(1)=0,f(2)=1,代入解析式得:(A−I)2=G2=⎝⎛000000001⎠⎞,G1=I−G2=⎝⎛100010000⎠⎞∴f(A)=f(1)G1+f(2)G2+f′(1)D1=f(1)⎝⎛100010000⎠⎞+f(2)⎝⎛000000001⎠⎞+f′(1)⎝⎛000100000⎠⎞f(x)=etx,f(1)=et,f(2)=e2t,f′(1)=tet可得etA=⎝⎛ettetete2t⎠⎞
10.5 幂0与Taylor求解f(A)(最一般化求解)
若有 A k = 0 ( k ≥ 2 ) A^k=0(k\ge 2) Ak=0(k≥2) ,则 f ( x ) f(x) f(x) 为任一解析式,则有
f ( A ) = f ( 0 ) + f ′ ( 0 ) A + f ′ ′ ( 0 ) 2 ! A 2 + ⋯ + f k − 1 ( 0 ) ( k − 1 ) ! A k − 1 \begin{aligned} f(A)=f(0)+f'(0)A+\frac{f''(0)}{2!}A^2+\cdots+\frac{f^{k-1}(0)}{(k-1)!}A^{k-1} \end{aligned} f(A)=f(0)+f′(0)A+2!f′′(0)A2+⋯+(k−1)!fk−1(0)Ak−1
- 对于平移幂0阵 ( A − a I ) k = 0 ( k ≥ 2 ) (A-aI)^k=0(k\ge 2) (A−aI)k=0(k≥2) , f ( x ) f(x) f(x) 为任一解析函数,则有公式 f ( A ) = f ( a ) I + f ′ ( a ) ( A − a I ) + f ′ ′ ( a ) 2 ! ( A − a I ) 2 + ⋯ + f ( a ) k − 1 ( k − 1 ) ! ( A − a I ) k − 1 f(A)=f(a)I+f'(a)(A-aI)+\frac{f''(a)}{2!}(A-aI)^2+\cdots+\frac{f(a)^{k-1}}{(k-1)!}(A-aI)^{k-1} f(A)=f(a)I+f′(a)(A−aI)+2!f′′(a)(A−aI)2+⋯+(k−1)!f(a)k−1(A−aI)k−1
eg
A 为 行 和 矩 阵 , λ ( A ) = { 0 , t r ( A ) − 0 } = { 0 , 0 } , 则 ( A − λ 1 I ) ( A − λ 2 I ) = A 2 = 0 f ( A ) = f ( 0 ) I + f ′ ( 0 ) A 令 f ( x ) = e t x , 则 f ( 0 ) = 1 , f ′ ( 0 ) = t , ⇒ f ( A ) = I + t A = ( 1 + t − t t 1 − t ) 令 f ( x ) = c o s ( t x ) , 则 f ( 0 ) = 1 , f ( 0 ) = − t s i n ( t x ) = 0 , ⇒ f ( A ) = I = ( 1 0 0 1 ) \begin{aligned} &A为行和矩阵,\lambda(A)=\{0,tr(A)-0\}=\{0,0\},则(A-\lambda_1I)(A-\lambda_2I)=A^2=0\\ &f(A)=f(0)I+f'(0)A\\ &令f(x)=e^{tx},则f(0)=1,f'(0)=t,\Rightarrow f(A)=I+tA=\left( \begin{matrix} 1+t&-t\\t&1-t \end{matrix} \right)\\ &令f(x)=cos(tx),则f(0)=1,f(0)=-tsin(tx)=0,\Rightarrow f(A)=I=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right) \end{aligned} A为行和矩阵,λ(A)={0,tr(A)−0}={0,0},则(A−λ1I)(A−λ2I)=A2=0f(A)=f(0)I+f′(0)A令f(x)=etx,则f(0)=1,f′(0)=t,⇒f(A)=I+tA=(1+tt−t1−t)令f(x)=cos(tx),则f(0)=1,f(0)=−tsin(tx)=0,⇒f(A)=I=(1001)
λ ( A ) = { 2 , 2 , 2 } , r ( A − 2 I ) = 2 ≠ 3 − 3 = 0 , A 不 是 单 阵 , 由 C a y l e y 公 式 , ( x − 2 ) 3 = 0 ⇒ ( A − 2 I ) 3 = 0 由 幂 0 公 式 与 泰 勒 公 式 , f ( A ) = f ( 2 ) I + f ′ ( 2 ) ( A − 2 I ) + f ′ ′ ( 2 ) 2 ! ( A − 2 I ) 2 令 f ( x ) = e t x , f ( 2 ) = e 2 t , f ′ ( 2 ) = t e 2 t , f ′ ′ ( 2 ) = t 2 e 2 t ∴ e t A = e 2 t I + t e 2 t ( A − 2 I ) + t 2 e 2 t 2 ( A − 2 I ) 2 = e 2 t [ I + t ( 0 1 0 0 0 1 0 0 0 ) + t 2 2 ( 0 0 1 0 0 0 0 0 0 ) ] = e 2 t ( 1 t t 2 2 0 1 t 0 0 1 ) 令 f ( x ) = s i n ( t x ) , f ( 2 ) = s i n 2 t , f ′ ( 2 ) = t c o s ( 2 t ) , f ′ ′ ( 2 ) = − t 2 s i n ( 2 t ) ∴ s i n ( t A ) = s i n ( 2 t ) I + t c o s ( 2 t ) ( A − 2 I ) − t 2 s i n ( 2 t ) ( A − 2 I ) 2 = = s i n ( 2 t ) ( 1 0 0 0 1 1 0 0 1 ) + t c o s ( 2 t ) ( 0 1 0 0 0 1 0 0 0 ) − t 2 ( 0 0 1 0 0 0 0 0 0 ) = ( s i n ( 2 t ) t c o s ( 2 t ) − t 2 2 s i n ( 2 t ) 0 s i n ( 2 t ) t c o s ( 2 t ) 0 0 s i n ( 2 t ) ) \begin{aligned} &\lambda(A)=\{2,2,2\},r(A-2I)=2\neq 3-3=0,A不是单阵,由Cayley公式,(x-2)^3=0\Rightarrow (A-2I)^3=0\\ &由幂0公式与泰勒公式,f(A)=f(2)I+f'(2)(A-2I)+\frac{f''(2)}{2!}(A-2I)^2\\ &令f(x)=e^{tx},f(2)=e^{2t},f'(2)=te^{2t},f''(2)=t^{2}e^{2t}\\ &\quad \therefore e^{tA}=e^{2t}I+te^{2t}(A-2I)+\frac{t^2e^{2t}}{2}(A-2I)^2=e^{2t}\left[I+t\left( \begin{matrix} 0&1&0\\0&0&1\\0&0&0 \end{matrix} \right)+\frac{t^2}{2}\left( \begin{matrix} 0&0&1\\0&0&0\\0&0&0 \end{matrix} \right)\right]\\ &\quad \quad \quad =e^{2t}\left( \begin{matrix} 1&t&\frac{t^2}{2}\\0&1&t\\0&0&1 \end{matrix} \right)\\ &令f(x)=sin(tx),f(2)=sin2t,f'(2)=tcos(2t),f''(2)=-t^2sin(2t)\\ &\quad \therefore sin(tA)=sin(2t)I+tcos(2t)(A-2I)-t^2sin(2t)(A-2I)^2=\\ &\quad \quad \quad =sin(2t)\left( \begin{matrix} 1&0&0\\0&1&1\\0&0&1 \end{matrix} \right)+tcos(2t)\left( \begin{matrix} 0&1&0\\0&0&1\\0&0&0 \end{matrix} \right)-t^2\left( \begin{matrix} 0&0&1\\0&0&0\\0&0&0 \end{matrix} \right)=\left( \begin{matrix} sin(2t)&tcos(2t)&-\frac{t^2}{2}sin(2t)\\ 0&sin(2t)&tcos(2t)\\ 0&0&sin(2t) \end{matrix} \right) \end{aligned} λ(A)={2,2,2},r(A−2I)=2=3−3=0,A不是单阵,由Cayley公式,(x−2)3=0⇒(A−2I)3=0由幂0公式与泰勒公式,f(A)=f(2)I+f′(2)(A−2I)+2!f′′(2)(A−2I)2令f(x)=etx,f(2)=e2t,f′(2)=te2t,f′′(2)=t2e2t∴etA=e2tI+te2t(A−2I)+2t2e2t(A−2I)2=e2t⎣⎡I+t⎝⎛000100010⎠⎞+2t2⎝⎛000000100⎠⎞⎦⎤=e2t⎝⎛100t102t2t1⎠⎞令f(x)=sin(tx),f(2)=sin2t,f′(2)=tcos(2t),f′′(2)=−t2sin(2t)∴sin(tA)=sin(2t)I+tcos(2t)(A−2I)−t2sin(2t)(A−2I)2==sin(2t)⎝⎛100010011⎠⎞+tcos(2t)⎝⎛000100010⎠⎞−t2⎝⎛000000100⎠⎞=⎝⎛sin(2t)00tcos(2t)sin(2t)0−2t2sin(2t)tcos(2t)sin(2t)⎠⎞
由 特 征 方 程 计 算 得 : λ ( A ) = { 2 , 2 , 2 } , ( A − 2 I ) ≠ 0 , 故 A 不 是 单 阵 , ( A − 2 I ) 2 = 0 故 可 用 泰 勒 求 解 矩 阵 函 数 , 解 析 式 为 f ( x ) = f ( 2 ) + f ′ ( 2 ) ( x − 2 ) , 矩 阵 函 数 为 f ( A ) = f ( 2 ) I + f ′ ( 2 ) ( A − 2 I ) 令 f ( x ) = e t x , f ( 2 ) = e 2 t , f ′ ( 2 ) = t e 2 t , f ′ ( 2 ) = t 2 e 2 t ⇒ e t A = e 2 t I + t e 2 t ( A − 2 I ) = e 2 t [ I + t ( 0 0 0 1 − 1 1 1 − 1 1 ) ] = e 2 t [ 1 0 0 t 1 − t t t − t 1 + t ] 令 f ( x ) = s i n ( t x ) , f ( 2 ) = s i n ( 2 t ) , f ′ ( 2 ) = t c o s ( 2 t ) ⇒ s i n ( t A ) = s i n ( 2 t ) I + t c o s ( 2 t ) ( A − 2 I ) = ( s i n ( 2 t ) 0 0 s i n ( 2 t ) 0 0 0 s i n ( 2 t ) ) + ( 0 0 0 t c o s ( 2 t ) − t c o s ( 2 t ) t c o s ( 2 t ) t c o s ( 2 t ) − t c o s ( 2 t ) t c o s ( 2 t ) ) = ( s i n ( 2 t ) 0 t c o s ( 2 t ) s i n ( 2 t ) − t c o s ( 2 t ) t c o s ( 2 t ) t c o s ( 2 t ) t c o s ( 2 t ) s i n ( 2 t ) + t c o s ( 2 t ) ) \begin{aligned} &由特征方程计算得:\lambda(A)=\{2,2,2\},(A-2I)\neq 0,故A不是单阵,(A-2I)^2=0\\ &故可用泰勒求解矩阵函数,解析式为f(x)=f(2)+f'(2)(x-2),矩阵函数为f(A)=f(2)I+f'(2)(A-2I)\\ &令f(x)=e^{tx},f(2)=e^{2t},f'(2)=te^{2t},f'(2)=t^2e^{2t}\\ &\quad \Rightarrow e^{tA}=e^{2t}I+te^{2t}(A-2I)=e^{2t}\left[I+t\left( \begin{matrix} 0&0&0\\1&-1&1\\1&-1&1 \end{matrix} \right)\right]=e^{2t}\left[ \begin{matrix} 1&0&0\\t&1-t&t\\t&-t&1+t \end{matrix} \right]\\ &令f(x)=sin(tx),f(2)=sin(2t),f'(2)=tcos(2t)\\ &\quad \Rightarrow sin(tA)=sin(2t)I+tcos(2t)(A-2I)=\left( \begin{matrix} sin(2t)&0&\\0&sin(2t)&0\\0&0&sin(2t) \end{matrix} \right)+\left( \begin{matrix} 0&0&0\\tcos(2t)&-tcos(2t)&tcos(2t)\\tcos(2t)&-tcos(2t)&tcos(2t) \end{matrix} \right)\\ &\quad \quad \quad \quad \quad \quad =\left( \begin{matrix} sin(2t)&0&\\tcos(2t)&sin(2t)-tcos(2t)&tcos(2t)\\tcos(2t)&tcos(2t)&sin(2t)+tcos(2t) \end{matrix} \right) \end{aligned} 由特征方程计算得:λ(A)={2,2,2},(A−2I)=0,故A不是单阵,(A−2I)2=0故可用泰勒求解矩阵函数,解析式为f(x)=f(2)+f′(2)(x−2),矩阵函数为f(A)=f(2)I+f′(2)(A−2I)令f(x)=etx,f(2)=e2t,f′(2)=te2t,f′(2)=t2e2t⇒etA=e2tI+te2t(A−2I)=e2t⎣⎡I+t⎝⎛0110−1−1011⎠⎞⎦⎤=e2t⎣⎡1tt01−t−t0t1+t⎦⎤令f(x)=sin(tx),f(2)=sin(2t),f′(2)=tcos(2t)⇒sin(tA)=sin(2t)I+tcos(2t)(A−2I)=⎝⎛sin(2t)000sin(2t)00sin(2t)⎠⎞+⎝⎛0tcos(2t)tcos(2t)0−tcos(2t)−tcos(2t)0tcos(2t)tcos(2t)⎠⎞=⎝⎛sin(2t)tcos(2t)tcos(2t)0sin(2t)−tcos(2t)tcos(2t)tcos(2t)sin(2t)+tcos(2t)⎠⎞
A − I = ( − 2 − 2 6 − 1 − 1 3 − 1 − 1 3 ) 为 秩 1 阵 , 可 知 λ ( A − I ) = { 0 , 0 , 0 } , 故 λ ( A ) = { 1 , 1 , 1 } , A − I ≠ 0 , 故 A 不 是 单 阵 ( A − I ) 2 = 0 , 故 可 写 解 析 函 数 f ( x ) = f ( 1 ) + f ′ ( 1 ) ( x − 1 ) , 矩 阵 函 数 为 f ( A ) = f ( 1 ) I + f ′ ( 1 ) ( A − I ) 令 f ( x ) = e t x , f ( 1 ) = e t , f ′ ( t ) = t e t ⇒ f ( A ) = f ( 1 ) I + f ′ ( 1 ) ( A − I ) = e t [ I + t ( − 2 − 2 6 − 1 − 1 3 − 1 − 1 3 ) ] = e t ( 1 − 2 t − 2 t 6 t − t 1 − t 3 t − t − t 1 + 3 t ) \begin{aligned} &A-I=\left( \begin{matrix} -2&-2&6\\-1&-1&3\\-1&-1&3 \end{matrix} \right)为秩1阵,可知\lambda(A-I)=\{0,0,0\},故\lambda(A)=\{1,1,1\},A-I\neq 0,故A不是单阵\\ &(A-I)^2=0,故可写解析函数f(x)=f(1)+f'(1)(x-1),矩阵函数为f(A)=f(1)I+f'(1)(A-I)\\ &令f(x)=e^{tx},f(1)=e^t,f'(t)=te^t\\ &\Rightarrow f(A)=f(1)I+f'(1)(A-I)=e^t\left[ I+t\left(\begin{matrix} -2&-2&6\\-1&-1&3\\-1&-1&3 \end{matrix} \right) \right]=e^t\left( \begin{matrix} 1-2t&-2t&6t\\-t&1-t&3t\\-t&-t&1+3t \end{matrix} \right) \end{aligned} A−I=⎝⎛−2−1−1−2−1−1633⎠⎞为秩1阵,可知λ(A−I)={0,0,0},故λ(A)={1,1,1},A−I=0,故A不是单阵(A−I)2=0,故可写解析函数f(x)=f(1)+f′(1)(x−1),矩阵函数为f(A)=f(1)I+f′(1)(A−I)令f(x)=etx,f(1)=et,f′(t)=tet⇒f(A)=f(1)I+f′(1)(A−I)=et⎣⎡I+t⎝⎛−2−1−1−2−1−1633⎠⎞⎦⎤=et⎝⎛1−2t−t−t−2t1−t−t6t3t1+3t⎠⎞
10.5.1 若当阵的矩阵函数
a. 若当阵
n 阶 上 三 角 A = ( a 1 0 a 1 ⋱ ⋱ ⋱ 1 a ) n × n , 为 n 阶 若 当 阵 , λ = a 为 n 重 根 , 若 a = 0 , 可 得 n 阶 0 根 若 当 阵 D = ( 0 1 0 0 1 ⋱ ⋱ ⋱ 1 0 ) n × n , 可 知 A − a I = D = ( 0 1 0 0 1 ⋱ ⋱ ⋱ 1 0 ) n × n \begin{aligned} &n阶上三角A=\left( \begin{matrix} a&1&&&0\\&a&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&a \end{matrix} \right)_{n\times n},为n阶若当阵,\lambda=a为n重根,\\ &若a=0,可得n阶0根若当阵D=\left( \begin{matrix} 0&1&&&0\\&0&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&0 \end{matrix} \right)_{n\times n},\\ &可知A-aI=D=\left( \begin{matrix} 0&1&&&0\\&0&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&0 \end{matrix} \right)_{n\times n} \end{aligned} n阶上三角A=⎝⎜⎜⎜⎜⎛a1a1⋱⋱⋱01a⎠⎟⎟⎟⎟⎞n×n,为n阶若当阵,λ=a为n重根,若a=0,可得n阶0根若当阵D=⎝⎜⎜⎜⎜⎛0101⋱⋱⋱010⎠⎟⎟⎟⎟⎞n×n,可知A−aI=D=⎝⎜⎜⎜⎜⎛0101⋱⋱⋱010⎠⎟⎟⎟⎟⎞n×n
对于n阶0根若当阵,有
b. n阶若当阵的矩阵函数
对于n阶若当阵 ( a 1 0 a 1 ⋱ ⋱ ⋱ 1 a ) \left( \begin{matrix} a&1&&&0\\&a&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&a \end{matrix} \right) ⎝⎜⎜⎜⎜⎛a1a1⋱⋱⋱01a⎠⎟⎟⎟⎟⎞ ,对任一解析函数 f ( x ) f(x) f(x) 有
eg
由 于 A 3 = 0 , 故 f ( A ) = ( f ( 2 ) f ′ ( 2 ) f ′ ′ ( 2 ) 2 ! f ( 2 ) f ′ ( 2 ) f ( 2 ) ) 令 f ( x ) = s i n ( t x ) , f ( 2 ) = s i n ( 2 t ) , f ′ ( 2 ) = t c o s ( 2 t ) , f ′ ′ ( 2 ) = − t 2 s i n ( 2 t ) ⇒ s i n ( t A ) = ( f ( 2 ) f ′ ( 2 ) f ′ ′ ( 2 ) 2 ! f ( 2 ) f ′ ( 2 ) f ( 2 ) ) = ( s i n ( 2 t ) t c o s ( 2 t ) − t 2 2 s i n ( 2 t ) s i n ( 2 t ) t c o s ( 2 t ) s i n ( 2 t ) ) \begin{aligned} &由于A^3=0,故f(A)=\left( \begin{matrix} f(2)&f'(2)&\frac{f''(2)}{2!}\\ &f(2)&f'(2)\\ &&f(2) \end{matrix} \right)\\ &令f(x)=sin(tx),f(2)=sin(2t),f'(2)=tcos(2t),f''(2)=-t^2sin(2t)\\ &\Rightarrow sin(tA)=\left( \begin{matrix} f(2)&f'(2)&\frac{f''(2)}{2!}\\ &f(2)&f'(2)\\ &&f(2) \end{matrix} \right)=\left( \begin{matrix} sin(2t)&tcos(2t)&-\frac{t^2}{2}sin(2t)\\ &sin(2t)&tcos(2t)\\ &&sin(2t) \end{matrix} \right) \end{aligned} 由于A3=0,故f(A)=⎝⎛f(2)f′(2)f(2)2!f′′(2)f′(2)f(2)⎠⎞令f(x)=sin(tx),f(2)=sin(2t),f′(2)=tcos(2t),f′′(2)=−t2sin(2t)⇒sin(tA)=⎝⎛f(2)f′(2)f(2)2!f′′(2)f′(2)f(2)⎠⎞=⎝⎛sin(2t)tcos(2t)sin(2t)−2t2sin(2t)tcos(2t)sin(2t)⎠⎞
令 f ( x ) = e t x , f ( A ) = ( e t a t e t a t 2 2 ! e t a ⋯ t k − 1 ( k − 1 ) ! e t a e t a t e t a ⋯ t k − 2 ( k − 2 ) ! e t a ⋱ ⋱ ⋮ e t a t e t a e t a ) \begin{aligned} 令f(x)=e^{tx},f(A)=\left( \begin{matrix} e^{ta}&te^{ta}&\frac{t^2}{2!}e^{ta}&\cdots &\frac{t^{k-1}}{(k-1)!}e^{ta}\\ &e^{ta}&te^{ta}&\cdots&\frac{t^{k-2}}{(k-2)!}e^{ta}\\ &&\ddots&\ddots&\vdots\\ &&&e^{ta}&te^{ta}\\ &&&&e^{ta} \end{matrix} \right) \end{aligned} 令f(x)=etx,f(A)=⎝⎜⎜⎜⎜⎜⎜⎛etatetaeta2!t2etateta⋱⋯⋯⋱eta(k−1)!tk−1eta(k−2)!tk−2eta⋮tetaeta⎠⎟⎟⎟⎟⎟⎟⎞
10.5.2 分块阵
eg
( 1 ) A = ( A 1 A 2 ) , A 1 = ( 1 1 0 1 ) , A 2 = ( 2 ) , A 1 为 若 当 阵 , 故 f ( A 1 ) = ( f ( 1 ) f ′ ( 1 ) 0 f ( 1 ) ) , f ( A 2 ) = ( f ( 2 ) ) , 故 f ( A ) = ( f ( 1 ) f ′ ( 1 ) 0 0 f ( 1 ) 0 0 0 f ( 2 ) ) 令 f ( x ) = e t x , ⇒ f ′ ( x ) = t e t x , f ( 1 ) = e t , f ′ ( 1 ) = t e t , f ( 2 ) = e 2 t ⇒ f ( A ) = ( e t t e t 0 0 e t 0 0 0 e 2 t ) , A 100 = ( 1 100 0 0 1 0 0 0 2 100 ) \begin{aligned} &(1)A=\left( \begin{matrix} A_1&\\&A_2 \end{matrix} \right),A_1=\left( \begin{matrix} 1&1\\0&1 \end{matrix} \right),A_2=\left( \begin{matrix} 2 \end{matrix} \right),\\ &A_1为若当阵,故f(A_1)=\left( \begin{matrix} f(1)&f'(1)\\0&f(1) \end{matrix} \right),f(A_2)=(f(2)),故f(A)=\left( \begin{matrix} f(1)&f'(1)&0\\0&f(1)&0\\0&0&f(2) \end{matrix} \right)\\ &令f(x)=e^{tx},\Rightarrow f'(x)=te^{tx},f(1)=e^t,f'(1)=te^{t},f(2)=e^{2t}\\ &\Rightarrow f(A)=\left( \begin{matrix} e^t&te^t&0\\0&e^t&0\\0&0&e^{2t} \end{matrix} \right),A^{100}=\left( \begin{matrix} 1&100&0\\0&1&0\\0&0&2^{100} \end{matrix} \right) \end{aligned} (1)A=(A1A2),A1=(1011),A2=(2),A1为若当阵,故f(A1)=(f(1)0f′(1)f(1)),f(A2)=(f(2)),故f(A)=⎝⎛f(1)00f′(1)f(1)000f(2)⎠⎞令f(x)=etx,⇒f′(x)=tetx,f(1)=et,f′(1)=tet,f(2)=e2t⇒f(A)=⎝⎛et00tetet000e2t⎠⎞,A100=⎝⎛10010010002100⎠⎞