第1周学习笔记:深度学习和pytorch基础
目录
一 视频学习
1.绪论
2.深度学习概述
二 代码学习
1.Pytorch基础练习
2.螺旋数据分类
一 视频学习
1.绪论
人工智能(Artificial Intelligence):使一部机器像人一样进行感知、认知、决策、执行的人工程序或系统
人工智能三个层面:
- 计算智能
- 感知智能:类似于人的视觉、听觉、触觉等感知能力
- 认知智能:逻辑推理,知识理解,决策思考
应用:金融,内容创作,机器人
知识工程(人工定义)vs机器学习(自动训练):
机器学习的定义:从数据中自动提取知识
模型分类
- 数据标记
- 监督学习:样本有标记。从数据中学习标记类别分界面(输入-输出的映射函数) ,适用于预测数据标记
- 无监督学习:样本没有标记。从数据中学习模式,适用于描述数据
- 半监督学习:部分数据标记已知。监督学习和无监督学习的混合
- 出发点:标记样本难以获取,无标记样本相对廉价
- 思路:假设未标记样本与标记样本独立同分布→包含关于数据分布的重要信息(聚类假设&流形假设)
- 强化学习:数据标记未知,但知道与输出目标相关的反馈——决策类问题
- 使用未标记的数据,但可以知道离目标越来越近还是越来越远(奖励反馈)
- 数据分布
- 参数模型:对数据有一个假设,可以用一个有固定数量参数的模型去解决它
- 非参数模型:不对数据分布进行假设,数据的所有统计特性都来源于数据本身
- 非参≠无参
- 建模对象
- 生成模型:对输入X和输出Y的联合分布P(X, Y)建模
- 先从数据中学习联合概率分布P(X,Y) ;然后利用贝叶斯公式求P(Y|X)
- 判别模型:对已知输入X条件下输出Y的条件分布P(Y|X)建模
- 生成模型:对输入X和输出Y的联合分布P(X, Y)建模
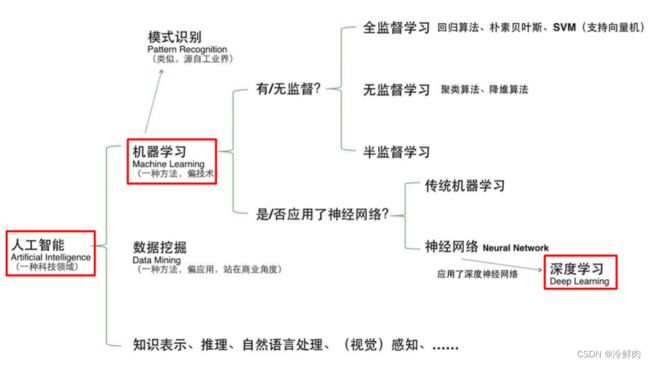
人工智能、机器学习和深度学习的关系:
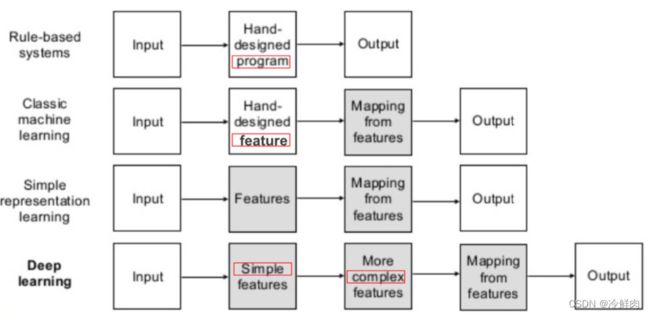
传统机器学习vs深度学习:
神经网络结构的发展:
深度学习的“不能”:
- 算法输出不稳定,容易被“攻击”(容易被人为噪声干扰)
- 模型复杂度高,难以纠错和调试
- 模型层级复合程度高,参数不透明
- 端到端训练方式对数据依赖性强,模型增量性差
- 专注直观感知类问题,对开放性推理问题无能为力(鹦鹉vs乌鸦)
- 人类知识无法有效引入进行监督,机器偏见难以避免(亚洲人黑人偏见)
深度学习——准确性高但解释性差
连接主义&符号主义
- 连接主义:自下而上,模拟人大脑的结构
- 符号主义:自上而下,代表专家系统
- 连接主义+符号主义:知识图谱和深度学习的结合
2.深度学习概述
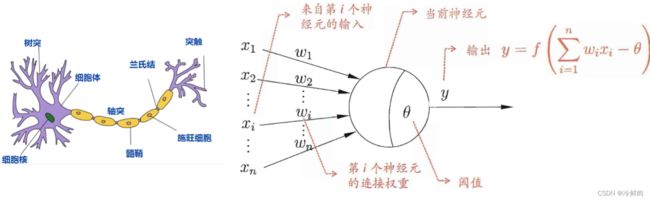
生物神经元的启发:
- 每个神经元都是一个多输入单输出的信息处理单元;
- 神经元具有空间整合和时间整合特性;
- 神经元输入分兴奋性输入和抑制性输入两种类型(权值正负模拟兴奋\抑制,大小模拟强度)
- 神经元具有阈值特性(输入和超过阈值θ,神经元被激活)
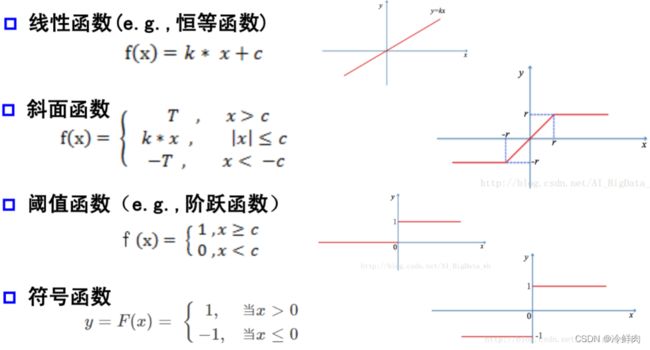
激活函数:
- 神经元继续传递信息、产生新连接的概率(超过阈值被激活,但不一定传递)
- 没有激活函数相当于矩阵相乘,得到的仍然是一个新的矩阵
- 常见激活函数如下:
单层感知器:
首个可以学习的人工神经网络,可以实现一些简单的与非或门
单层→多层感知器:
单层感知器解决不了非线性的分类问题(异或),复杂的逻辑单元可以通过组合简单的与或非单元来实现来实现,由此形成了多层的感知器。
万有逼近定理:
如果一个隐层包含足够多的神经元,三层前馈神经网络(输入-隐层-输出)能以任意精度逼近任意预定的连续函数。
- 为什么线性分类任务组合后可以解决非线性分类任务?
- 对于第二层感知器而言,看到的不是原始图像分布,而是被第一层感知器处理后的图像分布
当隐层足够宽时,双隐层感知器(输入-隐层1-隐层2-输出)可以逼近任意非连续函数,可以解决任何复杂的分类问题
神经网络每一层的作用:
- 神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换,将原始输入空间投影到线性可分的空间去分类/回归。
- 增加节点数:增加维度,即增加线性转换能力。
- 增加层数:增加激活函数的次数,即增加非线性转换次数
实验证明,瘦高的网络比矮胖的网络更有效。在神经元总数相当的情况下,增加网络深度可以比增加宽度带来更强的网络表示能力(产生更多的线性区域)。深度和宽度对函数复杂度的贡献是不同的,深度的贡献是指数增长的,而宽度的贡献是线性的。
梯度和梯度下降:
多元函数在每个点可以有多个方向,每个方向都可以计算导数,称为方向导数。梯度是一个向量,它的方向是最大方向导数的方向,它的模是方向导数的最大值。换句话来说,梯度的方向是函数值往极值点变化最快的方向。
梯度下降法是求解无约束最优化问题最常用的方法之一。梯度下降法用一阶泰勒展开式代替原函数,迭代计算原函数在当前取值邻域内的极值。具体的,函数迭代的每一步都朝着梯度的负方向,直到误差小于阈值。
神经网络的参数学习:误差反向传播(BP算法)
多层神经网络可看成是一个复合的非线性多元函数
深层神经网络的问题:梯度消失
误差经过每一项的sigmoid激活函数,可能会变得非常非常小
- 为什么有的时候单隐层可以解决的问题,加了多隐层之后反而解决不了了?
- 经过前向传播算出的损失,在反向传播的过程中可能会逐层越来越小,甚至可以忽略,由此造成靠前的参数不会发生变化,只有最后一层会发生更新
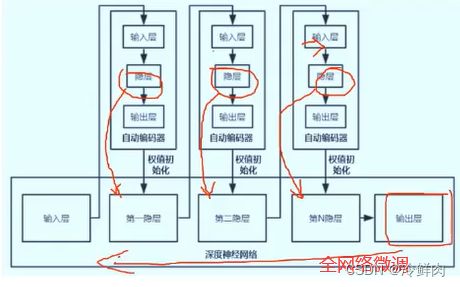
逐层预训练(layer-wise pre-training)
每次训练一层网络,逐层累加,在最后一层加入监督信息,从上到下做一次微调。经过逐层预训练后的解会更收敛,训练会更快
逐层预训练怎么实现——受限玻尔兹曼机和自编码器
自编码器(autoencoder):最小化重构误差
- 把自己的输入当作最后的输出(target=input),没有额外监督信息,无标签数据误差的来源是直接重构后信号与原输入相比得到
- 将input输入一个encoder编码器,就会得到一个code;加一个decoder解码器,输出信息,通过调整encoder 和decoder的参数,使得重构误差最小
- 自编码器一般是一个多层神经网络(最简单:三层) ,训练目标是使输出层与输入层误差最小;中间隐层是对输入比较好的表示,可以最大程度上代表原输入信号
堆叠自编码器(stacked autoencoder, SAE) :将多个自编码器得到的隐层串联,得到完整的神经网络。所有层预训练完成后,进行基于监督学习的全网络微调
受限玻耳兹曼机(RBM):
- 不同于自编码器,只是一个两层的网络(可见层v、隐藏层h),不同层之间全连接,层内无连接(二分图)
- 与感知器不同,RBM没有显式的重构过程:输入v,通过p(h|v)得到隐藏层h;输入h,通过p(v|h)得到v
- 是一种生成模型,需要从联合概率里求出两个方向的条件概率
- 玻尔兹曼这个词来自于能量分布,概率、能量和熵:有序,发生的概率小,熵小,能量高;无序,发生的概率大,熵大,能量低
堆叠RBM(DBM,深度信念网络):
一个DBN模型由若干个RBM堆叠而成,最后加一个监督层(如BP网络)。训练过程由低到高逐层训练:
- 最底部RBM以原始输入数据训练
- 将底部RBM抽取的特征作为顶部RBM的输入继续训练
- 重复这个过程训练尽可能多的RBM层
- 基于监督信息通过全局优化算法对网络进行微调,使模型收敛
DBN(Deep Belief Network) VS DBM (Deep Boltzmann Machine):DBM没有监督层,是若干个RBM的直接堆叠,是纯粹的无向图模型,每两层间互有反馈
一般玻尔兹曼机(BM):
- 是一个全网络,可见层和隐层内部结点之间可连接。具有很强大的无监督学习能力,能够学习数据中复杂的规则。
- 全连接图,复杂度很高,难以准确计算BM所表示的分布,难以抽样得到服从BM所表示分布的随机样本
| 自编码器 |
受限玻耳兹曼机 |
|
| 结构 |
编码和解码函数不同 |
共享权重矩阵,但有两个偏置向量 |
| 原理 |
自编码器通过非线性变换学习特征,是确定的,特征值可以为任何实数; |
RBM基于概率分布定义,高层表示为底层特征的条件概率,输出只有两种状态(未激活激活),用二进制0/1表示; |
| 训练优化 |
自编码器通过最损失函数L最小化重构输入数据,直接用BP优化求解 |
RBM基于最大似然,能量函数偏导无法直接计算,基于采样方法进行估计 |
| 模型类型 |
判别模型 |
生成模型 |
目前逐层预训练已经很少使用,玻尔兹曼机作为一种概率生成式模型应用到了协同滤波推荐、数据降维、时间序列降维问题;自编码器也经历了变种,正则自编码器(Regularized AE)应用于使提取的特征表达符合某种性质,稀疏自编码器(Sparse AE)应用于提取稀疏特征表达
二 代码学习
1.Pytorch基础练习
创建Tensor有多种方法,包括:ones, zeros, eye, arange, linspace, rand, randn, normal, uniform, randperm等等
import torch
x = torch.tensor(666) # 可以是一个数
x = torch.tensor([1,2,3,4,5,6]) # 可以是一维数组(向量)
x = torch.ones(2,3) # 可以是二维数组(矩阵)
x = torch.ones(2,3,4) # 可以是任意维度的数组(张量)
x = torch.empty(5,3) # 创建一个空张量
x = torch.rand(5,3) # 创建一个随机初始化的张量
x = torch.zeros(5,3,dtype=torch.long) # 创建一个全0的张量,里面的数据类型为long
# 基于现有的tensor,创建一个新tensor,
# 从而可以利用原有的tensor的dtype,device,size之类的属性信息
y = x.new_ones(5,3)
# 利用原来的tensor的大小,但是重新定义了dtype
z = torch.randn_like(x, dtype=torch.float) 基本运算包括: abs/sqrt/div/exp/fmod/pow ,及一些三角函数 cos/ sin/ asin/ atan2/ cosh,及 ceil/round/floor/trunc 等
布尔运算包括: gt/lt/ge/le/eq/ne,topk, sort, max/min
线性计算包括: trace, diag, mm/bmm,t,dot/cross,inverse,svd 等
import torch
# 创建一个 2x4 的tensor
m = torch.Tensor([[2, 5, 3, 7],[4, 2, 1, 9]])
print(m.size(0), m.size(1), m.size(), sep=' -- ')
# 返回m中元素的数量
print(m.numel())
# 返回第0行,第2列的数
print(m[0][2])
# 返回第1列的全部元素
print(m[:, 1])
# Create tensor of numbers from 1 to 5
v = torch.arange(1, 5)
v=v.float()
#点乘
m @ v
# Calculated by 1*2 + 2*5 + 3*3 + 4*7
m[[0], :] @ v
#把一个2x4的随机张量加到m上
m + torch.rand(2, 4)
# 转置,由 2x4 变为 4x2
print(m.t())
# 返回一个start=3, end=8, steps=20的一维张量
torch.linspace(3, 8, 20)数据类型的转变:
torch.long() 将tensor转换为long类型
torch.half() 将tensor转换为半精度浮点类型
torch.int() 将该tensor转换为int类型
torch.double() 将该tensor转换为double类型
torch.float() 将该tensor转换为float类型
torch.char() 将该tensor转换为char类型
torch.byte() 将该tensor转换为byte类型
torch.short() 将该tensor转换为short类型
绘制直方图:
from matplotlib import pyplot as plt
# matlabplotlib 只能显示numpy类型的数据,下面展示了转换数据类型,然后显示
# 注意 randn 是生成均值为 0, 方差为 1 的随机数
# 下面是生成 1000 个随机数,并按照 100 个 bin 统计直方图
plt.hist(torch.randn(1000).numpy(), 100);
# 当数据非常非常多的时候,正态分布会体现的非常明显
plt.hist(torch.randn(10**6).numpy(), 100);tensor的拼接:
# 创建两个 1x4 的tensor
a = torch.Tensor([[1, 2, 3, 4]])
b = torch.Tensor([[5, 6, 7, 8]])
# 在 0 方向拼接 (即在 Y 方各上拼接), 会得到 2x4 的矩阵
print( torch.cat((a,b), 0))
# 在 1 方向拼接 (即在 X 方各上拼接), 会得到 1x8 的矩阵
print( torch.cat((a,b), 1))2.螺旋数据分类
- 对样本进行初始化
3个类别,每个类别有1000个样本。使用torch.zeros()对样本矩阵进行初始化,根据公式划分出三类样本
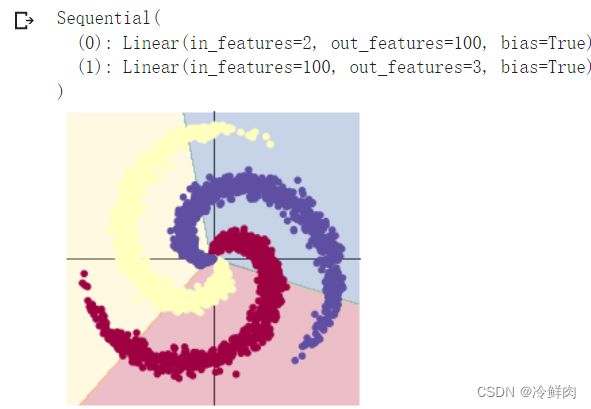
- 构建线性模型分类
关键代码如下:
learning_rate = 1e-3
lambda_l2 = 1e-5
# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
nn.Linear(D, H), #第一层输入为2(因为特征维度为主2),输出为100;
nn.Linear(H, C) #第二层输入为100(上一层的输出),输出为3(类别数)
)
model.to(device) # 把模型放到GPU上
# nn 包含多种不同的损失函数,这里使用的是交叉熵(cross entropy loss)损失函数
criterion = torch.nn.CrossEntropyLoss()
# 这里使用optim包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 开始训练
for t in range(1000):
# 把数据输入模型,得到预测结果
y_pred = model(X) #[3000, 3]
# 计算损失
loss = criterion(y_pred, Y)
#沿着第二个方向(即X方向)提取最大值。最大的那个值存在 score 中,所在的位置(即第几列的最大)保存在 predicted 中
score, predicted = torch.max(y_pred, 1)
#计算准确率
acc = (Y == predicted).sum().float() / len(Y)
print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
#清除单元格输出
display.clear_output(wait=True)
# 反向传播前把梯度置 0
optimizer.zero_grad()
# 反向传播优化
loss.backward()
# 更新全部参数
optimizer.step()为什么每一次反向传播前,都要把梯度清零?
- 因为PyTorch默认会对梯度进行累加。在反向传播时,如果不想先前的梯度对当前的梯度计算产生影响,就需要手动清零。Pytorch设计这种需要手动清零的方式,目的在于反向传播时,可以支持多种传播方式
训练1000个epoch效果如下,可以看出效果并不理想,对于较为复杂的非线性分类,线性模型难以实现准确分类。
- 构建两层神经网络分类
与上述模型的不同之处在于,在两层之间加入了一个 ReLU 激活函数
# 这里可以看到,和上面模型不同的是,在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)实验结果如下,在两层神经网络里加入 ReLU 激活函数以后,分类的准确率得到了显著提高。
- 更换激活函数
尝试将ReLU 激活函数更换为课件中所涉及、目前较为常用的激活函数,实验结果如下表所示
| 损失 | 准确率 | 分类效果 | |
| Sigmoid | 0.757981 | 0.515 | |
| Tanh | 0.301596 | 0.848 | |
| ReLU | 0.170588 | 0.953 | |
| LeakyReLU |
0.167449 | 0.954 |
由实验结果得出,将激活函数更换为LeakyReLU可以得到较好的实验效果。