Swin Transformer源码分析

swin transformer是什么这里就不在说明了，会点进来肯定是知道这个模型是做什么的。

直接看论文有些地方看的一知半解。这里直接从源码分析看下模型的具体实现

论文地址：https://arxiv.org/pdf/2103.14030v1.pdfhttps://arxiv.org/pdf/2103.14030v1.pdf

代码地址：https://github.com/microsoft/Swin-Transformerhttps://github.com/microsoft/Swin-Transformer

首先我们先看下模型结构对下面分析源码很有用处 

 首先图片 H * W * 3 经过一个 patch partition 缩小四倍 同道从 C 变成 48

后续在经过4个 Swin Transformer Block  但是这四个block由

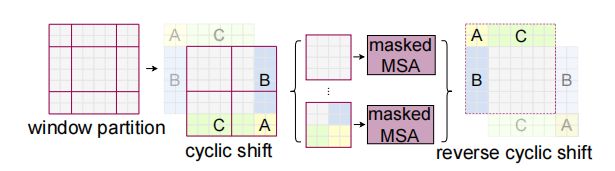
SW-MSA -- W-MSA 循环构成  从b图就可以看出来

W-MSA 全称 window  multi head self attention

SW-MSA 全称 shift  window  multi head self attention

下面进入源码分析

class SwinTransformer(nn.Module):
    
    def __init__(self, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
                 embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24],
                 window_size=7, mlp_ratio=4., qkv_bias=True, qk_scale=None,
                 drop_rate=0., attn_drop_rate=0., drop_path_rate=0.1,
                 norm_layer=nn.LayerNorm, ape=False, patch_norm=True,
                 use_checkpoint=False, **kwargs):
        super().__init__()

        self.num_classes = num_classes
        self.num_layers = len(depths)
        self.embed_dim = embed_dim
        self.ape = ape
        self.patch_norm = patch_norm
        self.num_features = int(embed_dim * 2 ** (self.num_layers - 1))
        self.mlp_ratio = mlp_ratio

        # split image into non-overlapping patches
        # 就是模型结构的 Patch Partition 图片变成 (B, H//4 * W//4, embed_dim)
        self.patch_embed = PatchEmbed(
            img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim,
            norm_layer=norm_layer if self.patch_norm else None)
        # 图像缩小4倍后的 patchers num
        num_patches = self.patch_embed.num_patches
        # 图像缩小4倍后的尺寸
        patches_resolution = self.patch_embed.patches_resolution
        self.patches_resolution = patches_resolution

        # absolute position embedding
        if self.ape:
            # 生成绝对位置编码 num_patches = H//4 * W//4 和经过PatchEmbed后的图片尺寸一致
            # 对应网络结构中的 linear embedding 网络结构
            self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
            # 绝对位置编码参数初始化
            trunc_normal_(self.absolute_pos_embed, std=.02)
        # 添加dropout
        self.pos_drop = nn.Dropout(p=drop_rate)

        # stochastic depth
        # 给网络层数每层设置随机dropout rate
        dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))]  # stochastic depth decay rule

        # build layers
        self.layers = nn.ModuleList()
        # 构建四层 w-msa 网络结构
        # input_resolution 表示每层会缩小 2**i_layer 倍 与给出的模型结构图展示的图像大小缩小倍数对应
        # depth block 深度
        # num_heads 多头数量
        # window_size 窗口大小
        # mlp_ratio Ratio of mlp hidden dim to embedding dim.
        # drop_path  dropout rate
        # downsample 下采样 前三个block 会进行下采样 第四个block 不会在进行下采样
        for i_layer in range(self.num_layers):
            layer = BasicLayer(dim=int(embed_dim * 2 ** i_layer),
                               input_resolution=(patches_resolution[0] // (2 ** i_layer),
                                                 patches_resolution[1] // (2 ** i_layer)),
                               depth=depths[i_layer],
                               num_heads=num_heads[i_layer],
                               window_size=window_size,
                               mlp_ratio=self.mlp_ratio,
                               qkv_bias=qkv_bias, qk_scale=qk_scale,
                               drop=drop_rate, attn_drop=attn_drop_rate,
                               drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
                               norm_layer=norm_layer,
                               downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
                               use_checkpoint=use_checkpoint)
            self.layers.append(layer)
        # 层归一化
        self.norm = norm_layer(self.num_features)
        # 平均池化
        self.avgpool = nn.AdaptiveAvgPool1d(1)
        # 网络输出
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()
        # 模型所以参数进行初始化
        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    @torch.jit.ignore
    def no_weight_decay(self):
        return {'absolute_pos_embed'}

    @torch.jit.ignore
    def no_weight_decay_keywords(self):
        return {'relative_position_bias_table'}

    def forward_features(self, x):
        # path_embed 就是模型结构的 Patch Partition 图片变成 (B, H//4 * W//4, embed_dim)
        x = self.patch_embed(x)
        # 是否使用绝对位置编码
        if self.ape:
            x = x + self.absolute_pos_embed
        x = self.pos_drop(x)
        # 经过4个 swin transformer block
        for layer in self.layers:
            x = layer(x)
        # 进行层归一化
        x = self.norm(x)  # B L C
        # 平局池化
        x = self.avgpool(x.transpose(1, 2))  # B C 1
        # 在第二个维度展平
        x = torch.flatten(x, 1)
        return x

    def forward(self, x):
        # 进行前向计算
        x = self.forward_features(x)
        # 模型最后输出用来进行分类 (b, c)
        x = self.head(x)
        return x

    def flops(self):
        """
        这个方法是用来计算模型性能的
        floating point operations per second
        """
        flops = 0
        flops += self.patch_embed.flops()
        for i, layer in enumerate(self.layers):
            flops += layer.flops()
        flops += self.num_features * self.patches_resolution[0] * self.patches_resolution[1] // (2 ** self.num_layers)
        flops += self.num_features * self.num_classes
        return flops

从上面我们可以看出  网络结构和论文中给出的图基本差不多 但是从代码看图网络结构更像是下面红色划分 

downsample=PatchMerging if (i_layer < self.num_layers - 1) else None

前三个block 会进行下采样 第四个block 不会在进行下采样  看上去更像是

4个 （block + patch merging）

 然后分析下

PatchEmbed 和 PatchMerging

class PatchEmbed(nn.Module):

    def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
        super().__init__()
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)
        patches_resolution = [img_size[0] // patch_size[0], img_size[1] // patch_size[1]]
        self.img_size = img_size
        self.patch_size = patch_size
        self.patches_resolution = patches_resolution
        self.num_patches = patches_resolution[0] * patches_resolution[1]

        self.in_chans = in_chans
        self.embed_dim = embed_dim
        # 用一个卷积操作来实现图像缩小四倍 kernel_size = 4  stride = patch_size
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
        if norm_layer is not None:
            self.norm = norm_layer(embed_dim)
        else:
            self.norm = None

    def forward(self, x):
        B, C, H, W = x.shape
        # FIXME look at relaxing size constraints
        assert H == self.img_size[0] and W == self.img_size[1], \
            f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
        # shape 变化 B, C, H, W --> B, C, h, w --> B, C, h * w --> B, h * w, c
        x = self.proj(x).flatten(2).transpose(1, 2)  # B Ph*Pw C
        # 进行层归一化
        if self.norm is not None:
            x = self.norm(x)
        return x

实现就是用一个  kernel_size = 4  stride = patch_size 的卷积操作来实现

nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

class PatchMerging(nn.Module):

    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        """
        x: B, H*W, C
        """
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x = x.view(B, H, W, C)
        # 这里实现path merging  图片缩小一半
        # 这里解释下 
        # 0::2 从 0 开始 隔一个点取一个值 
        # 1::2 从 1 开始 隔一个点取一个值
        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        # 在通道维度进行拼接
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C
        # 层归一化
        x = self.norm(x)
        # 降维到2 * dim 图片缩小一倍 通道维度增加一倍
        x = self.reduction(x)

        return x

可以从下面的表格看出 x0 x1 x2 x3 分别对应表格中 0 1 2 3 对应位置的点 最后在通道上合并 图片缩小一倍。

0	2	0	2
1	3	1	3
0	2	0	2
1	3	1	3

这里我们可以想一下 实现这种patch merge 方法有很多 比如 用2*2卷积来实现  、2*2平均池化等。 模型性能会提升还是降低？

接下来分析basic layer 层

class BasicLayer(nn.Module):
   
    def __init__(self, dim, input_resolution, depth, num_heads, window_size,
                 mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0.,
                 drop_path=0., norm_layer=nn.LayerNorm, downsample=None, use_checkpoint=False):

        super().__init__()
        self.dim = dim
        # 当前层的输入维度
        self.input_resolution = input_resolution
        # 当前层有多少个SwinTransformerBlock
        self.depth = depth
        self.use_checkpoint = use_checkpoint

        # build blocks
        # 构建深度为depth的block堆叠
        self.blocks = nn.ModuleList([
            # shift_size 需要注意下
            # 偶数个block是进行W-MSA 奇数进行SW-MSA   
            # SW-MSA - W-MSA - SW-MSA - W-MSA 的循环
            # 这样让输出特征包含 local window attention 和 跨窗口的 window attention
            SwinTransformerBlock(dim=dim, input_resolution=input_resolution,
                                 num_heads=num_heads, window_size=window_size,
                                 shift_size=0 if (i % 2 == 0) else window_size // 2,
                                 mlp_ratio=mlp_ratio,
                                 qkv_bias=qkv_bias, qk_scale=qk_scale,
                                 drop=drop, attn_drop=attn_drop,
                                 drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
                                 norm_layer=norm_layer)
            for i in range(depth)])

        # patch merging layer
        # 是否进行 patch merging  前三个block 执行patch merging 
        # 最后一个block 不会执行 patch merging 
        if downsample is not None:
            self.downsample = downsample(input_resolution, dim=dim, norm_layer=norm_layer)
        else:
            self.downsample = None

    def forward(self, x):
        # 进行前向传播
        for blk in self.blocks:
            if self.use_checkpoint:
                x = checkpoint.checkpoint(blk, x)
            else:
                x = blk(x)
        # 是否进行 patch merging 
        if self.downsample is not None:
            x = self.downsample(x)
        return x

进入 SwinTransformerBlock 我们主要分析 SW-MSA 的实现  W-MSA的实现很简单就是简单的局部 window multi head self attention 熟悉 Bert 和 transformer模型的人肯定很清楚 qkv三个矩阵的计算公式。

class SwinTransformerBlock(nn.Module):

    def __init__(self, dim, input_resolution, num_heads, window_size=7, shift_size=0,
                 mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0., drop_path=0.,
                 act_layer=nn.GELU, norm_layer=nn.LayerNorm):
        super().__init__()
        self.dim = dim
        self.input_resolution = input_resolution
        self.num_heads = num_heads
        # 默认大小 7
        self.window_size = window_size
        # 进行 SW-MSA shift-size 7//2=3
        # 进行 W-MSA shift-size 0
        self.shift_size = shift_size
        # multi self attention 最后神经网络的隐藏层的维度
        self.mlp_ratio = mlp_ratio
        if min(self.input_resolution) <= self.window_size:
            # if window size is larger than input resolution, we don't partition windows
            # 简单的判定 如果 最后图像缩小到比window size 还小 调整 window size 大小
            # 将 shift_size 赋值为 0  也就是说直接进行 W-MSA
            self.shift_size = 0
            self.window_size = min(self.input_resolution)
        assert 0 <= self.shift_size < self.window_size, "shift_size must in 0-window_size"
        # 层归一化
        self.norm1 = norm_layer(dim)
        # local window multi head self attention
        self.attn = WindowAttention(
            dim, window_size=to_2tuple(self.window_size), num_heads=num_heads,
            qkv_bias=qkv_bias, qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
        # dropout rate
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
        # 层归一化
        self.norm2 = norm_layer(dim)
        # 隐藏层维度增加的比率
        mlp_hidden_dim = int(dim * mlp_ratio)
        # 最后接一个多层感知机网络
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)

        # 可以看出 上面 结构是  layer normal +  W-MSA/SW-MSA + layer normal + mlp

        if self.shift_size > 0:
            # nW * B, window_size * window_size, C
            # calculate attention mask for SW-MSA
            # attention mask 的构成

            H, W = self.input_resolution
            img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1

            h_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            w_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))

            cnt = 0
            for h in h_slices:
                for w in w_slices:
                    img_mask[:, h, w, :] = cnt
                    cnt += 1

            mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1
            mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
            attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
            attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
        else:
            attn_mask = None

        self.register_buffer("attn_mask", attn_mask)

    def forward(self, x):
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"

        shortcut = x
        # 层归一化 如图所示  layer normal + W-MSA/SW-MSA
        x = self.norm1(x)
        x = x.view(B, H, W, C)

        # cyclic shift
        if self.shift_size > 0:
            # 进行 sw-msa 将数据进行变换
            shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
        else:
            shifted_x = x

        # partition windows
        # 将数据拆分成  n * window_size * window_size * c 的维度 方便进行self attention
        x_windows = window_partition(shifted_x, self.window_size)  # nW*B, window_size, window_size, C
        # 数据reshape成 (n, window_size * window_size, c) 送入 attention 层
        x_windows = x_windows.view(-1, self.window_size * self.window_size, C)  # nW*B, window_size*window_size, C

        # W-MSA/SW-MSA
        # 进行 multi head attention
        attn_windows = self.attn(x_windows, mask=self.attn_mask)  # nW*B, window_size*window_size, C

        # merge windows
        attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
        # 将数据维度退回到window_partition之前的维度
        shifted_x = window_reverse(attn_windows, self.window_size, H, W)  # B H' W' C

        # reverse cyclic shift
        if self.shift_size > 0:
            x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
        else:
            x = shifted_x
        x = x.view(B, H * W, C)

        # FFN
        x = shortcut + self.drop_path(x)
        x = x + self.drop_path(self.mlp(self.norm2(x)))

        return x

在分析代码前，我们先看下作者为什么会设计SW-MSA？

论文所述：

The shifted windows bridge the windows of the preceding layer, providing connections among them that signifificantly enhance modeling power

 简单来说，就是SW-MSA 是为了建立两个widow之间的桥梁设计的。也就是融合两个window之间的特征。极大的加强了模型的能力。

Wait. 这不就是类似滑动卷积核做卷积？真有你的哦！

接下来就是正题，源码中最难理解的地方来了。这里我先提前说下，作者是通过设计一个MASK来实现SW-MSA。

下面我们用一段代码模拟下：

import torch

def window_partition(x, window_size):
    H, W = x.shape
    x = x.view(H // window_size, window_size, W // window_size, window_size)
    windows = x.permute(0, 2, 1, 3).contiguous().view(-1, window_size, window_size)
    return windows

window_size = 3
shift_size = 3 // 2

data = torch.arange(81).view(9, 9)

shift_data = torch.roll(data, shifts=(-shift_size, -shift_size), dims=(0, 1))

mask = torch.zeros(9, 9)

h_slices = (slice(0, -window_size),
            slice(-window_size, -shift_size),
            slice(-shift_size, None))

w_slices = (slice(0, -window_size),
            slice(-window_size, -shift_size),
            slice(-shift_size, None))

cnt = 0
for h in h_slices:
    for w in w_slices:
        mask[h, w] = cnt
        cnt += 1

print('data', data)
print('shift_data', shift_data)
print('mask', mask)

mask_windows = window_partition(mask, window_size)  # nW, window_size, window_size
print('mask_windows', mask_windows)

mask_windows = mask_windows.view(-1, window_size * window_size)

print('reshape_mask_windows', mask_windows)

attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)

print('attn_mask', attn_mask)

attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

print('fill_attn_mask', attn_mask)

 data 输出

tensor([[ 0,  1,  2,  3,  4,  5,  6,  7,  8],
        [ 9, 10, 11, 12, 13, 14, 15, 16, 17],
        [18, 19, 20, 21, 22, 23, 24, 25, 26],
        [27, 28, 29, 30, 31, 32, 33, 34, 35],
        [36, 37, 38, 39, 40, 41, 42, 43, 44],
        [45, 46, 47, 48, 49, 50, 51, 52, 53],
        [54, 55, 56, 57, 58, 59, 60, 61, 62],
        [63, 64, 65, 66, 67, 68, 69, 70, 71],
        [72, 73, 74, 75, 76, 77, 78, 79, 80]])

shift_data 输出

tensor([[10, 11, 12, 13, 14, 15, 16, 17,  9],
        [19, 20, 21, 22, 23, 24, 25, 26, 18],
        [28, 29, 30, 31, 32, 33, 34, 35, 27],
        [37, 38, 39, 40, 41, 42, 43, 44, 36],
        [46, 47, 48, 49, 50, 51, 52, 53, 45],
        [55, 56, 57, 58, 59, 60, 61, 62, 54],
        [64, 65, 66, 67, 68, 69, 70, 71, 63],
        [73, 74, 75, 76, 77, 78, 79, 80, 72],
        [ 1,  2,  3,  4,  5,  6,  7,  8,  0]]) 

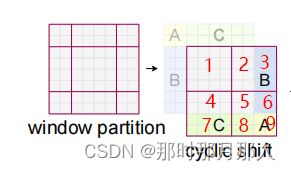
 上面两个输出刚好对应下图的 cyclic shift 

经过cyclic shift 后 的数据被分成了9份 如下图所示：每份之间的数据是互相可见的，其中1单独组成个window [2，3] 组成一个window 且 [2，3] 之间的数据互相不可见，但是 [2，3] 内的数据互相可见。同理 [4，7] 组成一个widnow。 [5, 6, 8, 9] 组成一个window 这是最特殊的一个window 由三部分shift 出去的数据和原先最后一个widnow剩下的数据组成。它们之间数据的可见性同上。

现在再看下面代码是不是瞬间理解了。

将mask分成上面的9份 分别用0~8设置

mask = torch.zeros(9, 9)
h_slices = (slice(0, -window_size),
            slice(-window_size, -shift_size),
            slice(-shift_size, None))
w_slices = (slice(0, -window_size),
            slice(-window_size, -shift_size),
            slice(-shift_size, None))
cnt = 0
for h in h_slices:
    for w in w_slices:
        mask[h, w] = cnt
        cnt += 1

mask 输出 就和上面分析的一摸一样

tensor([[0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 1., 1., 2.],
        [3., 3., 3., 3., 3., 3., 4., 4., 5.],
        [3., 3., 3., 3., 3., 3., 4., 4., 5.],
        [6., 6., 6., 6., 6., 6., 7., 7., 8.]])

window_partition 就是很简单的 reshape 操作 将器拆分成一个个window_size * window_size大小的window。从 (9, 9) - > (9, 3, 3)

def window_partition(x, window_size):
    H, W = x.shape
    x = x.view(H // window_size, window_size, W // window_size, window_size)
    windows = x.permute(0, 2, 1, 3).contiguous().view(-1, window_size, window_size)
    return windows

mask_windows = window_partition(mask, window_size)
mask_windows = mask_windows.view(-1, window_size * window_size)

mask_window 输出 9 * 9  每一行代表一个window共9个window  每一列代表 一个window内mask的值 window 大小 window_size * window_size （window_size  = 3）

tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [1., 1., 2., 1., 1., 2., 1., 1., 2.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [1., 1., 2., 1., 1., 2., 1., 1., 2.],
        [3., 3., 3., 3., 3., 3., 6., 6., 6.],
        [3., 3., 3., 3., 3., 3., 6., 6., 6.],
        [4., 4., 5., 4., 4., 5., 7., 7., 8.]])

 attn_mask 很多人想不明白这里是在干什么？没关系往后看，我们一步一步分析

attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)

mask_windows shape: (nw, 3 * 3)  nw: widown数量 3: 窗口大小

a = mask_windows.unsqueeze(1)  shape: (nw, 1, 3* 3)

b = mask_windows.unsqueeze(2)  shape: (nw,  3* 3 , 1)

由于广播机制  a, b 向对方的维度扩展 变成  (nw, 3* 3,  3* 3)

其中 a  b 在 dim = [1, 2] 维度上互为转置矩阵 a - b 类似于 行 减去 列 的值

此时每行的值是同一个window的的所有mask值，每一列的值代表当前window里第i个mask值

而mask值由上面分析 是由 0~8之间的数字组成，相同的表示互相可见。

如果两者相互可见，表示mask值一样，相减等于0。

此时 c = a - b  shape (nw, 3 * 3,  3 * 3)

c[i, j, k] 表示 第 i 个window  内 第 j 个 值 与 window 内 第 k 个 值是否互相可见  0 < j, k < 3 * 3

是不是感觉到熟悉了，这不就和self attention里面的 q * k.T后表示的意思一样嘛。 

下面就是将非0值用一个极大的负值替换。用来当 SW-MSA 的 mask 值。因为 self attention中是用softmax 来得到加权值 所以用一个大的负数来填充，得到的softmax值越接近0

attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

最后我们来看下 WindowAttention的实现。这里的实现只需要注意两点，就是pos编码设计和transform里面不同。

1. 设计了个相对位置编码bias表格

class WindowAttention(nn.Module):

    def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):

        super().__init__()
        self.dim = dim
        self.window_size = window_size  # Wh, Ww
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5

        # define a parameter table of relative position bias
        # 设计了一个相对位置编码  相对位置编码个数 (2 * window_size - 1) * (2 * window_size - 1)
        # 因为在一个 7 * 7 的 window内  相对位置范围 (-6, 6) 有 2 * 7 - 1 = 13 个
        # 所以对于二维数据 应该有 13 * 13 个 即 (2w - 1) * (2w - 1) 也就是相对坐标范围应该为 0 ~ (2w - 1) * (2w - 1) - 1
        self.relative_position_bias_table = nn.Parameter(
            torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 2*Wh-1 * 2*Ww-1, nH

        # get pair-wise relative position index for each token inside the window
        # 得到 window 内的表格坐标
        coords_h = torch.arange(self.window_size[0])
        coords_w = torch.arange(self.window_size[1])
        coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
        # 下面两行其实和 mask生成的是做的操作类似  也就是将数据展平后 广播后相减 得到相对坐标
        coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
        relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
        relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
        # 但是上面的相对坐标和定义的 relative_position_bias_table还对应不上 relative_coords 取值范围 (-w + 1) ~ (w - 1)
        # 所以在dim=[1, 2] 维度 才加上 self.window_size[0] - 1 取值范围 变成 0 ~ (2w - 2)
        relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
        relative_coords[:, :, 1] += self.window_size[1] - 1
        # 最后在 dim=2 的维度上 乘以 2w - 1 所以在这个维度上取值范围为 0 ~  (2w - 2) * (2w - 1) = (2w - 1)**2 - (2w - 1)
        relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
        # 最后求和后得到的相对坐标范围 0 ~ (2w - 1)**2 - (2w - 1) + (2w - 2) = (2w - 1)**2 - 1
        # OKay 到此为止终于得到范围为 0 ~ (2w - 1)**2 - 1 和 上面的 relative_position_bias_table对应上了
        # 所以每次只需要用相对索引去 relative_position_bias_table 表格中取值就行了
        relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
        self.register_buffer("relative_position_index", relative_position_index)

        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)

        trunc_normal_(self.relative_position_bias_table, std=.02)
        self.softmax = nn.Softmax(dim=-1)

2. 添加位置编码信息的位置不同，这里是在 计算 qk.T后在加上位置编码 bias

attn = (q @ k.transpose(-2, -1))

relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
    self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
attn = attn + relative_position_bias.unsqueeze(0)

其他的就和普通的 self attention 差不多 这里就不进行分析了。

到此为止源码基本分析完！

从代码上我们可以看到，Swin Transformer 基本上是抛弃了卷积操作。但一个SW-MSA确又看到了卷积的影子。 

SwinTransformV2 已经推出，用于大模型。对网络结构也做了一些调整。

后续我也会对SwinTransformV2源码 进行分析。