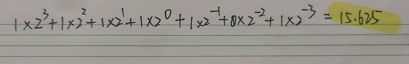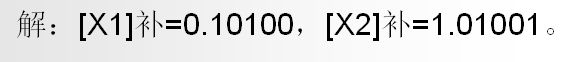计算机组成原理第二章练习(1)
计算机组成原理第二章练习(1)
2.1 进制
二进制数、八进制数、十六进制数转换为十进制数
十进制数转换为二进制
八进制转化为二进制(二转八一样蝶,还有十六转二,二转十六)
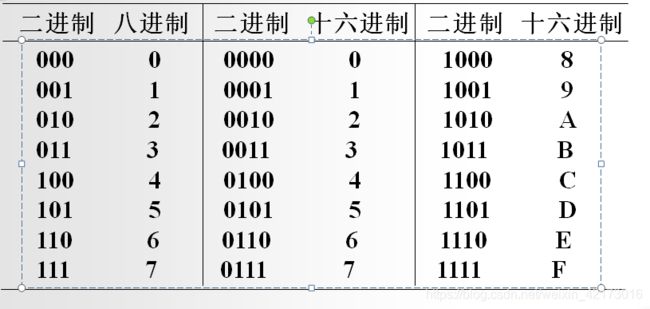
附:(这个进制转换表要会自己推理)
2.2计算机码制
注意:反码未在计算机中实际使用,仅是一种过渡码制
采用补码进行加减法运算,在计算机中只需要一套实现加法运算的线路,从而简化了计算机内部硬件电路的结构
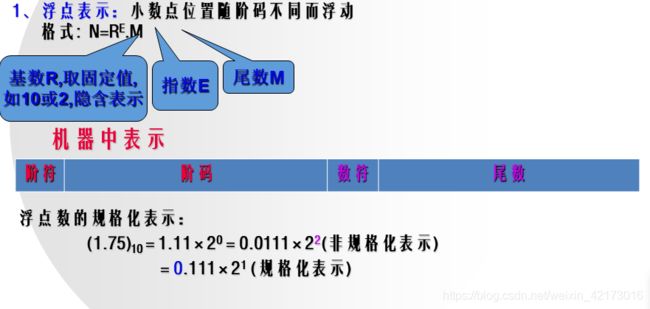
2.3 浮点数的表示方法(有点麻烦,多练习)
练习(1)
[例1]将(100.25)10转换为短浮点数格式.
解: (100.25)10=(1100100.01)2=1.10010001×26
s=0 M=10010001000000000000000
E=127+6=133=10000101
故:短浮点数代码为:
0,10000101,10010001000000000000000
图解:
v一、选择题
v1.运算器的主要功能时进行()
vA、逻辑运算 B、算术运算 C、 逻辑运算和算术运算 D、只作加法
v2.运算器虽有许多部件组成,但核心部件是()
vA、数据总线 B、算术逻辑运算单元 C、 多路开关 D、累加寄存器
v3.ALU属于()部件。
v A、运算器 B、控制器 C、存储器 D、寄存器
【解析:
算术逻辑单元(arithmetic and logic unit) 是能实现多组算术运算和逻辑运算的组合逻辑电路,简称ALU。 算术逻辑运算单元处于 运算器
】
v4.某机字长32位。其中1位符号位,31位表示尾数。若用 定点整数表示,则 最大正整数为______。
v A. +(231-1) B. +(230-1) C. +(231+1) D. +(230+1)
【
解析:
用定点 整数的话,然后又说机字长32位,所以最大的就是0111111111...111(31个1)
所以是2的31次方-1。
】
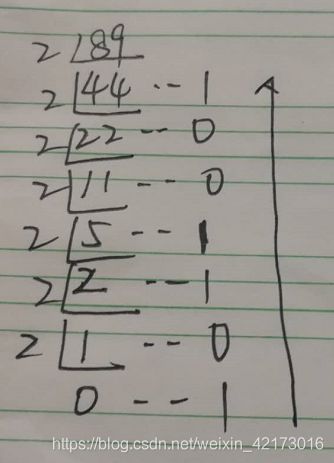
v5.十进制数89对应的二进制数是( )
v A、1011001 B、1011100 C、1001010 D、1001101
【
】
v6.若二进制数为1111.101,则相应的十进制数为( )
v A、15.625 B、15.5 C、14.625 D、14.5
【解析:
】
v7.在机器数( )中,零的表示形式是唯一的。
vA、原码 B、补码 C、补码和移码 D、原码和反码
v8.设X= —0.1011,则[X]补为______。
vA.1.1011 B.1.0100 C.1.0101 D.1.1001
【解析:
先转为真值,1.1011。后转为反码,1.0100。最后+1变成补码。
】
v9. 在小型或微型计算机里,普遍采用的字符编码是( )
vA. BCD码 B. 16进制 C. 格雷码 D. ASCⅡ码
v10. 已知X<0且[X]原 = X0.X1X2…Xn,则[X]补可通过( )求得。
v A.各位求反,末位加1 B.求补 C.除X0外求补 D.[X]反-1
v二、简答题
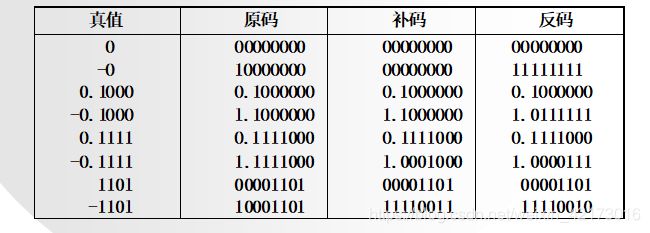
v1、设机器数的字长8位(含1位符号位),分别写出下列各二进制数的原码、补码和反码:
0,-0,0.1000,-0.1000,0.1111,-0.1111,1101,-1101
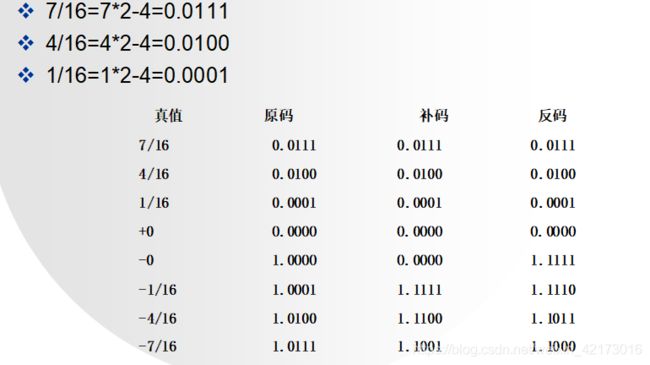
v2.写出下列各数的原码、补码和反码:7/16,4/16,1/16,±0,-7/16,-4/16,-1/16。
7/16=是7转化为2进制111,然后右移4个单位
v3.已知下列数的原码表示,分别写出它们的补码表示:[X1]原=O.10100,[X2]原=l.10111。
v4.已知下列数的补码表示,分别写出它们的真值:[X1]补=O.10100,[X2]补=1.10111
v5.若浮点数x的IEEE754标准存储格式为(41360000)16,求该规格化浮点数所表示的十进制数值(默认:尾数用原码表示,指数用非标准移码表示)。(重点关注)
先将(41360000)16转化为二进制S=0 E=100 0001 0 M=011 0110 0000 0000 0000 0000
可知公式v x=(-1)S×1.M×2e