点云配准论文阅读笔记--3d-dnt博士论文

点云配准系列

点云配准1：配准基础及icp算法
点云配准2：icp算法在PCL1.10.0上的实现+源码解析
点云配准3：3d-ndt算法在pcl上的实现以及参数设置
点云配准4：cloudcompare的使用以及点云配准功能
点云配准5：4pcs算法在pcl上的实现
点云配准6：tricp算法在pcl上的实现
点云配准论文阅读笔记–Efficient Variants of the ICP Algorithm
点云配准论文阅读笔记–Comparing ICP variants on real-world data sets
点云配准论文阅读笔记–(4PCS)4-Points Congruent Sets for Robust Pairwise Surface Registration
点云配准论文阅读笔记–3d-dnt博士论文

本文内容

3d-ndt的博士论文：
The Three-Dimensional Normal-Distributions Transform - an Efficient Representation for Registration,Surface Analysis, and Loop Detection
下载地址：share_noel/papers/The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection.pdf
https://blog.csdn.net/qq_41102371/article/details/125646840
建议读一遍原文，没懂的地方再结合着网络上的博客来看。
本篇博客关注点是博士论文里面的用3d-ndt进行点云配准的部分，且包含由个人理解，如有错漏敬请指正。
pcl中使用3d-ndt实现点云配准见：点云配准三：3d-ndt算法在pcl上的实现以及参数设置

摘要

本文将normal-distributions transform（NDT）因应用于扫描配准，定位，回环检测以及表面结构分析。对原始数据使用ndt后，扫描表面由具有一阶和二阶导数的分段光滑函数表示，这种表示具有很多特性。
使用光滑函数来表示 让一些例如牛顿法的标准数值优化方法 来进行配准成为可能。本论文将Biber的2d-ndt扩展至3维，并介绍了一些改进。通过使用多分辨率离散技术和三线性插值，可以克服基本配准算法中存在的离散化问题。将3d-ndt与icp配准进行了比较。实验数据包含真实数据和仿真数据。相对于icp，本文扩展的3d-ndt算法在大部分情况下，对于初始位姿较差的配准表现更快，更准确更鲁棒。
本文还提出颜色信息点云的3d-ndt配准，基于表面的回环检测。

chapter1 introduction

在很多情况下，因为遮挡、太大、或目标本身是碎片，单个扫描不能获取整个区域。因此需要将多个部分配准在一起构成完整的模型。为了配准两个扫描点云，必须找到每个点云正确的位置和方向，即位姿。配准的任务就是寻找最佳的位姿。成对配准是指在两次扫描的表面之间有一些重叠的情况下，找到使一次扫描与另一次扫描最佳对齐的姿势的过程。给出两次扫描之间相对姿态差的初始估计值，局部配准算法试图改进该估计值。一个好的扫描配准算法应该对初始位姿误差较大是鲁棒的，并能快速产生精确的姿态。扫描配准可进一步用于机器人领域的位姿跟踪。利用扫描数据的NDT表示，可以使用数值优化文献中的标准方法（如牛顿法）来执行扫描配准。

1.1 Contributions

3D-NDT surface representation：
应用3d-ndt于配准，回环检测，表面形状分析。
3D-NDT registration with extensions：
利用扫描数据的NDT表示，可以使用数值优化文献中的标准方法（如牛顿法）来执行扫描配准。通过使用多分辨率离散技术和三线性插值，可以克服基本配准算法中存在的离散化问题。
…

1.2 outline

chapter2介绍一些重要的概念，包括配准问题，旋转表示，降采样策略。
chapter3介绍硬件设备
chapter4介绍用于实验的数据采集平台
Part II是关于配准问题。相关工作在chapter5讨论，chapter6、7是3d-ndt及其变体算法。
Part III是3d-ndt的进一步应用。…
chapter10是本论文的总结，包含现有的一些公开问题和未来的研究方向。
最后是附录。附录A是本文用到的概念。B是3d-ndt使用的3d转换函数。C给出了更完整的实验结果图片。

chapter2 常用概念

2.1 点、位姿

点：用向量$x$表示其在空间中的位置
位姿（pose）：位姿是配准和定位的核心。本文中的pose是位置和方向的结合。更具体说，位姿是表示为三维坐标中的旋转和平移。

2.2 旋转

欧拉角（Euler angles）：欧拉角是三维旋转中常用的表示，表示绕着三个主轴x,y,x的连续旋转。比如：
$$[{\varphi }_x,{\varphi }_x,{\varphi }_x]\text{\hspace{1em}(2.1)}$$

表示一个旋转变换的组合。首先绕着z轴旋转${\varphi }_z$，再绕着y轴旋转${\varphi }_y$，最后绕着x轴旋转${\varphi }_x$。旋转顺序不一定非得z-y-x，也可以是x-y-z等。
欧拉角非常容易理解和实现，但是也有缺点：主要是欧拉角并不总是唯一的，有的情况下，可能会发生万向节锁，其中某个自由度会丢失。万向节锁可以这么理解：当第二个角处于某个临界值时，第一和第三个角度的变化是不可区分的。比如按x-y-z旋转，先绕x轴旋转${\varphi }_x$，当第二个角为${\varphi }_y$等于90°时，此时z轴已经和x轴重叠，万向节锁就发生了。关于万向节锁的理解可以参考下面的博文：
关于万向节死锁(Gimbal Lock)
【Unity编程】欧拉角与万向节死锁（图文版）
一个策略是，使用欧拉角时，以最大的旋转角开始。
旋转矩阵：
$$R_x{R}_y{R}_z=\left[\begin{array}{ccc}{c}_y{c}_z& c_y{s}_z& -s_y\\ s_x{s}_y{c}_z-c_x{s}_z& s_x{s}_y{s}_z+c_x{c}_z& s_x{c}_y\\ c_x{s}_y{c}_z& c_x{s}_y{s}_z-s_x{c}_z& c_x{c}_y\end{array}\right]\text{\hspace{1em}(2.2)}$$
其中，$c_i=cos{\varphi }_i$，$s_i=sin{\varphi }_i$。
另外还有四元数表示法（Quaternions），和用一个标量角与单位长度的三维向量描述：$(r,\varphi )$
在chapter6的配准工作中，将会使用欧拉角z-y-x，因为在配准的过程中角度相对较小，基本不会遇到万向节锁。

2.3 配准

成对配准是在两个扫描之间的相对姿态差未知的情况下匹配两个扫描的问题。给定两次具有一定重叠度的扫描，配准算法的输出是对变换的估计，当两次扫描正确匹配时，将使一次扫描（称为当前扫描）进入另一次扫描（参考扫描）坐标系中的正确姿势。
对比与全局曲面匹配算法，局部配准以给定的初始位姿开始在姿态空间进行局部搜索。如果初始位姿与与最优位姿差距太大的话，可能会陷入局部最优而找到错误的空间变换。

2.4 采样

为提升速度，实际上通常对数据进行降采样。
降采样的方法有很多，最简单的是均匀降采样，即从扫描数据中抽取n个点，或均匀随机地选点。在这种情况下，“一致”并不对应于点的均匀分布，而是对应于选择某个点的概率。
在许多情况下，尤其是在走廊和隧道中进行扫描时，在扫描仪位置附近的点分布比在更远的地方要密集得多。如果以均匀随机的方式对点进行采样，则采样的子集将具有类似的不均匀分布。在扫描远端的重要几何结构中，很少或根本没有采样点，导致配准不良。为了克服这个问题，通常使用某种形式的空间分布采样，以确保整个扫描体积的采样密度均匀。在目前的工作中，这样做的方式是创建一个网格结构的细胞大小相等，并把扫描点在相应的细胞。此采样网格的单元大小通常在0.1到0.2 m之间。从随机单元中提取一个随机点，直到达到所需的点数。如果单元的分布足够，此策略将使点分布均匀。

chapter5 扫描配准领域的相关工作

5.1 icp

对两重叠的点云，icp迭代地最小化它们之间各点的距离平方和来得到精确的位姿。
对于icp算法可参考之前的博文：
点云配准一：配准基础及icp算法
icp的一个局限性是，最近邻点通常不对应于扫描表面上的同一点，尤其是当两次扫描相距很远时。在ICP的成功应用中，由于其迭代性质，它仍然收敛到一个有用的解。搜索最近点是算法执行时耗时最多的地方。图5.1显示了一次ICP迭代中最近点的配对。

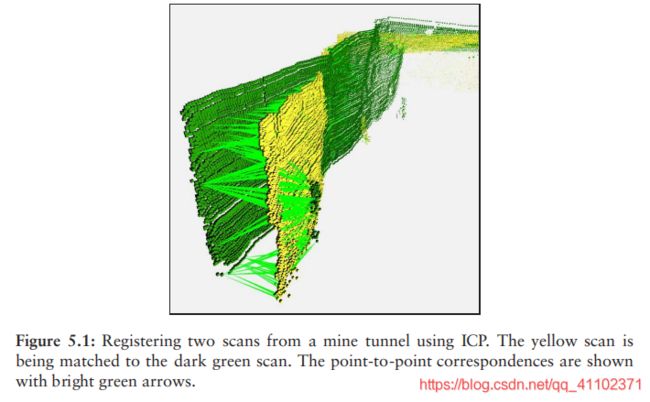
对点对进行加权是有益的，为更可能对应于相同曲面点的点对赋予更多权重。一个合理的加权标准是将权重设置为与点到点距离成反比，这样距离较远的点的权重比近邻点低。但是，对于隧道或道路数据，这种线性加权会降低性能。因为沿墙和天花板的大多数点通常都会很好地对齐，它们的影响将大于距离较大的点对，而这些距离较大的点对与 角点 和 其他对于获得良好匹配很重要的特征 相对应。
除了执行任何加权外，还应完全拒绝某些异常值对。点对抑制可以看作是点对加权的一种特殊情况。一个常见的标准是拒绝距离超过某个阈值的所有点对。此外，应始终拒绝包含参考扫描边界点的点对。否则，来自数据非重叠部分的点可能导致系统的“阻力”偏差-见图5.2。然而，点云数据的边界点难以确定。在先前发表的工作中[66]，我们使用了一个减少的距离阈值来拒绝离群值：从一个大的距离阈值开始，并在每次迭代中将其减小到零。使用这种方法的基本原理是，在早期迭代中，用较大距离隔开的点对可以使扫描更近。在以后的迭代中，点彼此相距很远的对很可能是不正确的对应关系，而不仅仅是初始姿态估计中的大误差造成的结果，因此应该予以拒绝。然而，加权和拒绝策略的最佳选择取决于数据的特性。在这项工作中进行的实验（如附录C所示）表明，这种距离阈值的减小实际上使 ICP在许多情况下对较大的初始姿态误差的 鲁棒性 降低。

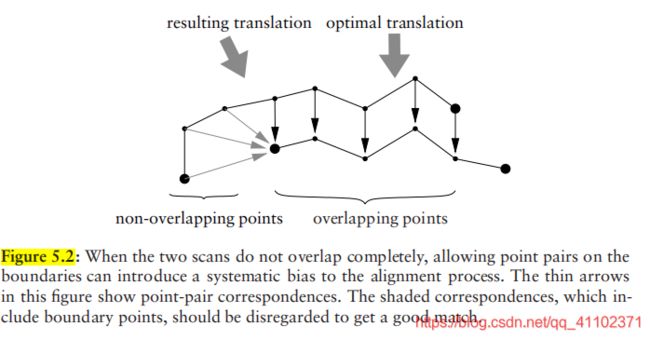
icp的速度瓶颈是最近邻搜索。icp的算法复杂度为O(nm)，其中m是参考点云的点数，n是当前点云的点数。使用kd树进行最近邻搜索可将算法复杂度降至O(nlogm)。

5.5 ndt算法

Biber和Straßer[7]介绍了二维数据配准的正态分布变换（NDT）方法。该算法的关键是参考扫描的表示。不是直接将当前扫描与参考扫描点匹配，而是通过正态分布的线性组合来模拟在特定位置找到曲面点的可能性。
正态分布给出了参考扫描的分段光滑表示，具有连续的一阶和二阶导数。使用这种表示法，可以应用标准的数值优化方法进行配准，例如牛顿法。
由于参考扫描中的点不直接用于匹配，因此不需要计算代价昂贵的ICP最近邻搜索。计算正态分布是一个一次性的任务，在一次通过参考扫描点的过程中完成。

chapter6 The normal-distributions transform

6.1 用ndt表示曲面

正态分布变换可以描述为一种紧表示曲面的方法。它首先由Biber和Straßer于2003年提出[7]，作为二维扫描配准的一种方法。该变换将一个点云映射到一个光滑的曲面表示，该曲面表示为一组局部概率密度函数（PDF），每个局部概率密度函数描述曲面的一部分形状。
该算法的第一步是将扫描占用的空间细分为一个网格单元（二维为正方形，三维为立方体）。根据单元内的点分布，为每个单元计算PDF。每个单元中的PDF可以解释为单元内表面点$x$的生成过程。换言之，假设$x$的位置是从这个分布中提取的。假设参考扫描表面点的位置是由D维正态随机过程生成的，则测量$x$的可能性为

$$p(x)=\frac{1}{(2\pi {)}^{D/2}\sqrt{\left|\Sigma \right|}}exp\left(-\frac{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}{2}\right)\text{\hspace{1em}(6.1)}$$
式中，$\mu$ 和 $\Sigma$ 表示 当前扫描点云的某一点$x$ 所在的参考点云单元的 平均向量 和 协方差矩阵。$(2\pi {)}^{D/2}{\sqrt{\left|\Sigma \right|}}^{-1}$是缩放因子，使函数积分为1，在实际应用中，可以用常数c0代替。平均值和协方差计算如下：
$$\mu =\frac{1}{m}\sum _{k=1}^m{y}_k,\text{\hspace{1em}(6.2)}$$$$\Sigma =\frac{1}{m-1}\sum _{k=1}^m(y_k-\mu )-(y_k-\mu {)}^T,\text{\hspace{1em}(6.3)}$$
其中$y_{k=1,...,m}$是单元中包含的参考扫描点的位置。
正态分布给出了点云的分段光滑表示，具有连续导数。每个PDF都可以看作是局部曲面的近似图像，描述了曲面的位置、方向和平滑度。二维激光扫描及其相应的正态分布如图6.1所示。图6.2显示了矿井隧道扫描的三维正态分布。


本文的工作聚焦于正态分布，因此让我们看看单变量和多边正态分布的特性。
一维的情况下，正态分布随机变量$x$有一个确定的期望值$\mu$，关于该值的不确定性用方差$\sigma$表示。
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp\left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)\text{\hspace{1em}(6.4)}$$
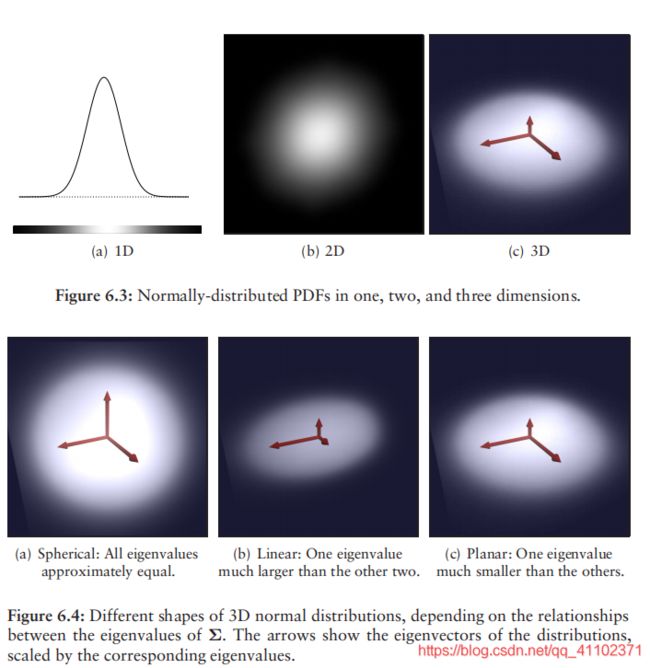
在多维情况下，均值和方差用均值向量$\mu$和协方差矩阵$\Sigma$来描述。对角元素的协方差表示各对角变量的协方差。图6.3显示了一维、二维和三维正态分布。
在二维和三维情况下，可以通过协方差矩阵的特征向量和特征值来评估曲面的方向和平滑度。特征向量描述了分布的主要成分；也就是说，一组与变量协方差的主方向相对应的正交向量。根据方差的比例，二维正态分布可以是点形（如果方差相似）或线型（如果其中一个比另一个大得多），或介于两者之间的任何形式。在3D情况下，如图6.4所示，正态分布可以描述一个点或一个球体（如果所有方向上的方差大小相似）、一条直线（如果一个方向的方差远大于另两个方向的方差）或平面（如果一个方向的方差远小于另两个方向的方差）。

6.2 NDT scan registration

使用NDT进行配准的目标是寻找当前点云最优的位姿，来使当前扫描点位于参考扫描表面的可能性最大化。待优化的参数，即当前扫描的位姿估计的旋转和平移；可以编码到向量$p$中。当前扫描表示为点云$\chi =\{x_1,...,x_n\}$。假设有一个空间变换函数$T(p,x)$，它通过位姿$p$在空间中移动一个点$x$。给定扫描点的PDF（例如，方程式6.1），最佳姿势$p$应为使似然函数最大化.
$$\Psi =\prod _{k=1}^{n}p(T(p,x_k))\text{\hspace{1em}(6.5)}$$
当前参数向量的NDT得分函数$s(p)$为
$$s(p)=-\sum _{k=1}^n\tilde{p}(T(p,x_k))\text{\hspace{1em}(6.5)}$$

似然函数要求协方差矩阵的逆，${\Sigma }^{-1}$。当一个单元中的点完全共面或共线时，协方差矩阵是奇异的，不能求逆。在三维情况下，由三个或更少的点计算的协方差矩阵总是奇异的。因此，仅为包含5个以上点的单元计算PDF。
牛顿算法可以用来寻找使$s(p)$最优化的参数$p$。牛顿法迭代地求解方程$H\Delta p=-g$，其中$H$和$g$是$s(p)$的Hessian矩阵和梯度向量。在每次迭代中，将增量$\Delta p$加到当前姿态估计中，使$p\leftarrow p+\Delta p$.

算法2描述了怎样用NDT来配准两个点云$\chi$和$\gamma$。

对于NDT配准，我自己的理解是：
NDT是将点云用一个光滑的曲面表示，该曲面表示为一组局部概率密度函数（PDF），每个局部概率密度函数描述曲面的一部分形状。也就是每个局部就是一个单元网格，每个网格有一个PDF。
将参考点云使用空间单元划分，若单元里的点数超过5个（原因上面已讲），则用NDT表示该单元。求取每个单元的均值向量$\mu$：
$$\mu =\frac{1}{m}\sum _{k=1}^m{y}_k,\text{\hspace{1em}(6.2)}$$
以及协方差矩阵$\Sigma$：
$$\Sigma =\frac{1}{m-1}\sum _{k=1}^m(y_k-\mu )-(y_k-\mu {)}^T,\text{\hspace{1em}(6.3)}$$
然后将该单元的PDF表示出来：
$$p(x)=\frac{1}{(2\pi {)}^{D/2}\sqrt{\left|\Sigma \right|}}exp\left(-\frac{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}{2}\right)\text{\hspace{1em}(6.1)}$$
这里的$x$是当前扫描中的某一个点。
举个例子，我们都知道一维正态分布的函数形式：
$$p(x)=\frac{1}{\sigma \sqrt{2\pi }}exp\left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)\text{\hspace{1em}(6.4)}$$
如果我们知道了数据的期望$\mu$和方差$\sigma$，那么上式就是确定的函数了，我们再带入一个数据x，就可以知道它的概率密度了。
同理，我们知道了多维正态分布的形式：
$$f(x)=\frac{1}{(2\pi {)}^{D/2}\sqrt{\left|\Sigma \right|}}exp\left(-\frac{(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}{2}\right)$$
其中D是维度。
在知道了期望值和方差之后，那么上式也是确定的。对一个单元来说，这就相当于把它里面离散的点的期望和方差求出来，然后带入连续的多维正态分布函数$f(x)$，这就有了上面说的将离散的点云映射到一个光滑的曲面表示。现在已知一个数据点$x$，将其带入上述已知的分布函数，就能求出该点的概率密度$p(x)$了。现在是有来自当前扫描点云的数据点$x$,找到其在参考点云中所处哪个cell，然后将该点带入该cell已知的分布函数，然后使用牛顿法优化使得所有经过空间变换后的点$T(p,x_k)$的$p(T(p,x_k))$之和最大，也就是最大化$s(p)$:
$$s(p)=-\sum _{k=1}^n\tilde{p}(T(p,x_k))\text{\hspace{1em}(6.5)}$$
所得的结果就是空间旋转变换。
关于牛顿法优化的过程，以及涉及到的一阶二阶导数也就是雅各比矩阵和海森矩阵，这几篇博文讲得比较清楚。
NDT（Normal Distributions Transform）算法原理与公式推导：
这篇博客很值得一看，下图红框中的式子就是$H\Delta p=-g$的由来

激光SLAM——第四节（激光SLAM的前端配准方法）：
二维NDT中Jacobian矩阵的由来

还有这些也是帮助理解的博客：
对向量求导
二次型求导的推导
海森矩阵
Jacobian矩阵的理解
多维高斯分布是如何由一维发展而来的？

参考

Magnusson, Martin. (2009). The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection.
Magnusson M，Lilienthal A，Duckett T.Scan registration for autonomous mining vehicles using 3D-NDT：Research articles[M].[S.l.]：John Wiley and Sons Ltd，2007：803-827.
Peter Biber and Wolfgang Straßer. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), pages 2743–2748, Las Vegas, USA, October 2003.
参考博客文中已列出

完

边学边用，如有错漏，敬请指正
--------------------------------------------------------------------------------------------诺有缸的高飞鸟202012