学习LOAM笔记——特征点提取与匹配

学习LOAM笔记——特征点提取与匹配

兜兜转转一圈，最近又开始接触一些和SLAM相关的工作，LOAM是一个非常经典的激光SLAM框架，LOAM和VLOAM至今还在kitti榜上有着不错的表现，从这篇博客开始，我开始着手对LOAM以及LOAM相关的算法进行一次深入的学习，欢迎大家来多交流。

在视觉SLAM领域，特征点提取是一个从一开始就有的一个模块，而在激光SLAM领域，以我的理解，前端最开始演进的是类似于ICP和NDT这样一些直接匹配算法，而从LOAM开始，算法开始从激光点中提取3D特征点，3D特征点在我很早之前的一篇博客视觉SLAM总结——视觉特征子综述中就有过总结，但是当时看到的3D特征点大多复杂而实时性不高，在LOAM算法的前端设计的特征点提取算法简洁而快速，保证了精度和实时性。

关于特征点提取算法我主要参考的是A-LOAM的代码，同时还简单过了下Livox-LOAM和M-LOAM的代码：

在A-LOAM中，首先是对输入的激光点按照激光线进行分类，然后在激光线上计算每一个点的曲率，按照曲率提线点和面点，后端则将前后帧的线点和面点转到同一坐标系下后按照最近邻搜索进行匹配；

在Livox-LOAM中，操作大同小异，不同的地方主要在于，在A-LOAM中处理的是圆柱激光，因此激光线是平行线，而Livox-LOAM中处理的是Livox激光，其激光线是花瓣状，两者在分类过程中就有所不同，除此之外，Livox-LOAM中，算法还对接近视角边缘的点、反射强度过大或者过小的点和平面夹角过小的点进行了过滤；

在M-LOAM中，M-LOAM中处理的方式就是分开处理单个激光，然后再将特征点组合到一起，看这个算法我之前，我是想了解下多个激光雷达激光线混在一起后怎么去获得激光点的曲率，是不是必须先对激光点按照激光先进行分类才能计算曲率呢？看样子好像是的哦

下面以A-LOAM为例，整理下特征点提取的算法和代码，具体如下

1. 特征点提取

A-LOAM中特征点提取一共分为如下三步：

1.1 对激光点按线束分类

按照激光雷达的线束模型，每一个线束称为一个scan，一帧线束组成一帧sweep，首先我们需要计算每个激光在激光雷达坐标系下的角度，按照角度阈值对激光点进行线束归类，并同时将特征点归一化到$\pi$和$-\pi$之间，方便后面计算，这个归一化过程说起来简单，但是实际上是比较繁杂的，因为每个sweep不一定是从0度开始，也不一定是在0度结束，扫描一圈的角度差也不一定是$2\pi$，因此代码中加了很多判断条件来处理该问题。

if (endOri - startOri > 3 * M_PI)   //将角度限制在-PI和PI之间
{
    endOri -= 2 * M_PI;
}
else if (endOri - startOri < M_PI)
{
    endOri += 2 * M_PI;
}

bool halfPassed = false;
int count = cloudSize;
PointType point;
std::vector<pcl::PointCloud<PointType>> laserCloudScans(N_SCANS); //将激光雷达点按扫描线进行归类
for (int i = 0; i < cloudSize; i++)
{
    point.x = laserCloudIn.points[i].x;
    point.y = laserCloudIn.points[i].y;
    point.z = laserCloudIn.points[i].z;

    float angle = atan(point.z / sqrt(point.x * point.x + point.y * point.y)) * 180 / M_PI; //计算激光雷达点倾斜角度，按照角度进行分类
    int scanID = 0;

    if (N_SCANS == 16)
    {
        scanID = int((angle + 15) / 2 + 0.5);
        if (scanID > (N_SCANS - 1) || scanID < 0)
        {
            count--;
            continue;
        }
    }
    else if (N_SCANS == 32)
    {
        scanID = int((angle + 92.0/3.0) * 3.0 / 4.0);
        if (scanID > (N_SCANS - 1) || scanID < 0)
        {
            count--;
            continue;
        }
    }
    else if (N_SCANS == 64)
    {   
        if (angle >= -8.83)
            scanID = int((2 - angle) * 3.0 + 0.5);
        else
            scanID = N_SCANS / 2 + int((-8.83 - angle) * 2.0 + 0.5);

        if (angle > 2 || angle < -24.33 || scanID > 50 || scanID < 0)
        {
            count--;
            continue;
        }
    }
    else
    {
        printf("wrong scan number\n");
        ROS_BREAK();
    }

    float ori = -atan2(point.y, point.x); //下面应该是对角度进行归一化
    if (!halfPassed)
    { 
        if (ori < startOri - M_PI / 2)
        {
            ori += 2 * M_PI;
        }
        else if (ori > startOri + M_PI * 3 / 2)
        {
            ori -= 2 * M_PI;
        }

        if (ori - startOri > M_PI)
        {
            halfPassed = true;
        }
    }
    else
    {
        ori += 2 * M_PI;
        if (ori < endOri - M_PI * 3 / 2)
        {
            ori += 2 * M_PI;
        }
        else if (ori > endOri + M_PI / 2)
        {
            ori -= 2 * M_PI;
        }
    }

    float relTime = (ori - startOri) / (endOri - startOri); //计算相对时间
    point.intensity = scanID + scanPeriod * relTime;
    laserCloudScans[scanID].push_back(point); 
}

1.2 计算激光点曲率

曲率的计算公式如下：
$$c=\frac{1}{|S|\cdot \Vert {\mathbf{X}}_{(k,i)}^L\Vert }\sum _{j\in S,j\ne i}\Vert {\mathbf{X}}_{(k,i)}^L-{\mathbf{X}}_{(k,j)}^L\Vert$$
代码中对该公式进行了简化，选取当前点同一线束上左右各5个点进行曲率计算，具体代码如下：

 pcl::PointCloud<PointType>::Ptr laserCloud(new pcl::PointCloud<PointType>());
 for (int i = 0; i < N_SCANS; i++)
 { closestPointScanID
     scanStartInd[i] = laserCloud->size() + 5;// 记录每个scan的开始index，忽略前5个点
     *laserCloud += laserCloudScans[i];
     scanEndInd[i] = laserCloud->size() - 6;// 记录每个scan的结束index，忽略后5个点，开始和结束处的点云scan容易产生不闭合的“接缝”，对提取edge feature不利
 }

 printf("prepare time %f \n", t_prepare.toc());

 for (int i = 5; i < cloudSize - 5; i++)
 { 
     float diffX = laserCloud->points[i - 5].x + laserCloud->points[i - 4].x + laserCloud->points[i - 3].x + laserCloud->points[i - 2].x + laserCloud->points[i - 1].x - 10 * laserCloud->points[i].x + laserCloud->points[i + 1].x + laserCloud->points[i + 2].x + laserCloud->points[i + 3].x + laserCloud->points[i + 4].x + laserCloud->points[i + 5].x;
     float diffY = laserCloud->points[i - 5].y + laserCloud->points[i - 4].y + laserCloud->points[i - 3].y + laserCloud->points[i - 2].y + laserCloud->points[i - 1].y - 10 * laserCloud->points[i].y + laserCloud->points[i + 1].y + laserCloud->points[i + 2].y + laserCloud->points[i + 3].y + laserCloud->points[i + 4].y + laserCloud->points[i + 5].y;
     float diffZ = laserCloud->points[i - 5].z + laserCloud->points[i - 4].z + laserCloud->points[i - 3].z + laserCloud->points[i - 2].z + laserCloud->points[i - 1].z - 10 * laserCloud->points[i].z + laserCloud->points[i + 1].z + laserCloud->points[i + 2].z + laserCloud->points[i + 3].z + laserCloud->points[i + 4].z + laserCloud->points[i + 5].z;

     cloudCurvature[i] = diffX * diffX + diffY * diffY + diffZ * diffZ;  // 这里应该是计算曲率
     cloudSortInd[i] = i;
     cloudNeighborPicked[i] = 0;// 点有没有被选选择为feature点
     cloudLabel[i] = 0;// Label 2: corner_sharp
                       // Label 1: corner_less_sharp, 包含Label 2
                       // Label -1: surf_flat
                       // Label 0: surf_less_flat， 包含Label -1，因为点太多，最后会降采样
 }

1.3 根据曲率提取特征点

为了使得在一周360度上有均匀的约束,，我们将一条激光线平均分为6块， 将块内的点按曲率大小排列，将曲率最大的2个点作为corner sharp点，曲率最大的前20个点作为corner less sharp点，曲率最小的4个点作为surf flat点，除上述三种类型外的其余的点以及surf flat点作为surf less flat点，surf less flat点相对会较多，因此最后还会对surf less flat点进行一次下采样，那么为什么要分为这四类点呢？

原因是在前后帧进行匹配时，当前帧的corner shape点会与前一帧的corner less shape点进行匹配，而surf flat点会与surf less flat点进行匹配，将曲率最大的点与曲率相对大的点进行匹配可以增加匹配成功概率。

for (int i = 0; i < N_SCANS; i++)// 按照scan的顺序提取4种特征点
{
    if( scanEndInd[i] - scanStartInd[i] < 6)// 如果该scan的点数少于7个点，就跳过
        continue;
    pcl::PointCloud<PointType>::Ptr surfPointsLessFlatScan(new pcl::PointCloud<PointType>);
    for (int j = 0; j < 6; j++)// 将该scan分成6小段执行特征检测
    {
        int sp = scanStartInd[i] + (scanEndInd[i] - scanStartInd[i]) * j / 6;// subscan的起始index
        int ep = scanStartInd[i] + (scanEndInd[i] - scanStartInd[i]) * (j + 1) / 6 - 1;// subscan的结束index

        TicToc t_tmp;
        std::sort (cloudSortInd + sp, cloudSortInd + ep + 1, comp);// 根据曲率有小到大对subscan的点进行sort
        t_q_sort += t_tmp.toc();

        int largestPickedNum = 0;
        for (int k = ep; k >= sp; k--)// 从后往前，即从曲率大的点开始提取corner feature
        {
            int ind = cloudSortInd[k]; 

            if (cloudNeighborPicked[ind] == 0 &&
                cloudCurvature[ind] > 0.1)// 如果该点没有被选择过，并且曲率大于0.1
            {
                largestPickedNum++;
                if (largestPickedNum <= 2)// 该subscan中曲率最大的前2个点认为是corner_sharp特征点
                {                        
                    cloudLabel[ind] = 2;
                    cornerPointsSharp.push_back(laserCloud->points[ind]);
                    cornerPointsLessSharp.push_back(laserCloud->points[ind]);
                }
                else if (largestPickedNum <= 20)// 该subscan中曲率最大的前20个点认为是corner_less_sharp特征点
                {                        
                    cloudLabel[ind] = 1; 
                    cornerPointsLessSharp.push_back(laserCloud->points[ind]);
                }
                else
                {
                    break;
                }

                cloudNeighborPicked[ind] = 1;// 标记该点被选择过了

                // 与当前点距离的平方 <= 0.05的点标记为选择过，避免特征点密集分布
                for (int l = 1; l <= 5; l++)
                {
                    float diffX = laserCloud->points[ind + l].x - laserCloud->points[ind + l - 1].x;
                    float diffY = laserCloud->points[ind + l].y - laserCloud->points[ind + l - 1].y;
                    float diffZ = laserCloud->points[ind + l].z - laserCloud->points[ind + l - 1].z;
                    if (diffX * diffX + diffY * diffY + diffZ * diffZ > 0.05)
                    {
                        break;
                    }

                    cloudNeighborPicked[ind + l] = 1;
                }
                for (int l = -1; l >= -5; l--)
                {
                    float diffX = laserCloud->points[ind + l].x - laserCloud->points[ind + l + 1].x;
                    float diffY = laserCloud->points[ind + l].y - laserCloud->points[ind + l + 1].y;
                    float diffZ = laserCloud->points[ind + l].z - laserCloud->points[ind + l + 1].z;
                    if (diffX * diffX + diffY * diffY + diffZ * diffZ > 0.05)
                    {
                        break;
                    }

                    cloudNeighborPicked[ind + l] = 1;
                }
            }
        }

        // 提取surf平面feature，与上述类似，选取该subscan曲率最小的前4个点为surf_flat
        int smallestPickedNum = 0;
        for (int k = sp; k <= ep; k++)
        {
            int ind = cloudSortInd[k];

            if (cloudNeighborPicked[ind] == 0 &&
                cloudCurvature[ind] < 0.1)
            {

                cloudLabel[ind] = -1; 
                surfPointsFlat.push_back(laserCloud->points[ind]);

                smallestPickedNum++;
                if (smallestPickedNum >= 4)
                { 
                    break;
                }

                cloudNeighborPicked[ind] = 1;
                for (int l = 1; l <= 5; l++)
                { 
                    float diffX = laserCloud->points[ind + l].x - laserCloud->points[ind + l - 1].x;
                    float diffY = laserCloud->points[ind + l].y - laserCloud->points[ind + l - 1].y;
                    float diffZ = laserCloud->points[ind + l].z - laserCloud->points[ind + l - 1].z;
                    if (diffX * diffX + diffY * diffY + diffZ * diffZ > 0.05)
                    {
                        break;
                    }

                    cloudNeighborPicked[ind + l] = 1;
                }
                for (int l = -1; l >= -5; l--)
                {
                    float diffX = laserCloud->points[ind + l].x - laserCloud->points[ind + l + 1].x;
                    float diffY = laserCloud->points[ind + l].y - laserCloud->points[ind + l + 1].y;
                    float diffZ = laserCloud->points[ind + l].z - laserCloud->points[ind + l + 1].z;
                    if (diffX * diffX + diffY * diffY + diffZ * diffZ > 0.05)
                    {
                        break;
                    }

                    cloudNeighborPicked[ind + l] = 1;
                }
            }
        }

        
        // 其他的非corner特征点与surf_flat特征点一起组成surf_less_flat特征点
        for (int k = sp; k <= ep; k++)
        {
            if (cloudLabel[k] <= 0)
            {
                surfPointsLessFlatScan->push_back(laserCloud->points[k]);
            }
        }
    }
}					

2. 特征点匹配

特征点匹配分为scan-to-scan以及scan-to-map两种，这两种类型的匹配基本原理都是一致的，都是转到相同坐标系下采用最近邻的方式获取，不同的是scan-to-scan更加简单粗暴，而scan-to-map会更加复杂鲁棒，具体如下：

2.1 scan-to-scan中的特征点匹配

在scan-to-scan的匹配过程中，首先是将所有特征点转到当前帧其实时刻坐标系下，再将前后帧特征点转到同一坐标系下，后者可以通过IMU或者匀速运动模型获得初始位姿：

1. 对于corner sharp点O来说就是寻找匹配帧中，corner less sharp点中最近的点A以及和点A位于相邻线束（不一定是相邻一帧）最近的点B，残差即点O到直线AB的距离；
2. 对于surf flat点P来说就是就是寻找匹配帧中，surf less flat点中最近的点A，以及和A位于同一线束的点B，以及和A位于相邻线束的点C，残差即点P到平面ABC的距离；

上述过程中提到的最近点A都是KD-Tree搜索最近邻获得的，具体代码如下，非常的简介明了
线特征：

// 基于最近邻原理建立corner特征点之间关联，find correspondence for corner features
for (int i = 0; i < cornerPointsSharpNum; ++i)
{para_q
    TransformToStart(&(cornerPointsSharp->points[i]), &pointSel);// 将当前帧的corner_sharp特征点O_cur，从当前帧的Lidar坐标系下变换到上一帧的Lidar坐标系下（记为点O，注意与前面的点O_cur不同），以利于寻找corner特征点的correspondence
    kdtreeCornerLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis);// kdtree中的点云是上一帧的corner_less_sharp，所以这是在上一帧
                                                                                    // 的corner_less_sharp中寻找当前帧corner_sharp特征点O的最近邻点（记为A）

    int closestPointInd = -1, minPointInd2 = -1;
    if (pointSearchSqDis[0] < DISTANCE_SQ_THRESHOLD)// 如果最近邻的corner特征点之间距离平方小于阈值，则最近邻点A有效
    {
        closestPointInd = pointSearchInd[0];
        int closestPointScanID = int(laserCloudCornerLast->points[closestPointInd].intensity);

        double minPointSqDis2 = DISTANCE_SQ_THRESHOLD;
        // 寻找点O的另外一个最近邻的点（记为点B） in the direction of increapointSearchIndsing scan line
        for (int j = closestPointInd + 1; j < (int)laserCloudCornerclosestPointIndLast->points.size(); ++j)// laserCloudCornerLast 来自上一帧的corner_less_sharp特征点,由于提取特征时是
        {                                                                                   // 按照scan的顺序提取的，所以laserCloudCornerLast中的点也是按照scanID递增的顺序存放的
            // if in the same scan line, continue
            if (int(laserCloudCornerLast->points[j].intensity) <= closestPointScanID)// intensity整数部分存放的是scanID
                continue;

            // if not in nearby scans, end the loop
            if (int(laserCloudCornerLast->points[j].intensity) > (closestPointScanID + NEARBY_SCAN))
                break;

            double pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) *
                                    (laserCloudCornerLast->points[j].x - pointSel.x) +
                                (laserCloudCornerLast->points[j].y - pointSel.y) *
                                    (laserCloudCornerLast->points[j].y - pointSel.y) +
                                (laserCloudCornerLast->points[j].z - pointSel.z) *
                                    (laserCloudCornerLast->points[j].z - pointSel.z);

            if (pointSqDis < minPointSqDis2)// 第二个最近邻点有效,更新点B
            {
                // find nearer point
                minPointSqDis2 = pointSqDis;
                minPointInd2 = j;
            }
        }

        // 寻找点O的另外一个最近邻的点B in the direction of decreasing scan line
        for (int j = closestPointInd - 1; j >= 0; --j)
        {
            // if in the same scan line, continue
            if (int(laserCloudCornerLast->points[j].intensity) >= closestPointScanID)
                continue;

            // if not in nearby scans, end the loopclosestPointInd
            if (int(laserCloudCornerLast->points[j].intensity) < (closestPointScanID - NEARBY_SCAN))
                break;

            double pointSqDis = (laserCloudCornerLast->points[j].x - pointSel.x) *
                                    (laserCloudCornerLast->points[j].x - pointSel.x) +
                                (laserCloudCornerLast->points[j].y - pointSel.y) *
                                    (laserCloudCornerLast->points[j].y - pointSel.y) +
                                (laserCloudCornerLast->points[j].z - pointSel.z) *
                                    (laserCloudCornerLast->points[j].z - pointSel.z);

            if (pointSqDis < minPointSqDis2)// 第二个最近邻点有效，更新点B
            {
                // find nearer point
                minPointSqDis2 = pointSqDis;
                minPointInd2 = j;
            }
        }
    }
    if (minPointInd2 >= 0) // both closestPointInd and minPointInd2 is valid
    {                      // 即特征点O的两个最近邻点A和B都有效
        Eigen::Vector3d curr_point(cornerPointsSharp->points[i].x,
                                   cornerPointsSharp->points[i].y,
                                   cornerPointsSharp->points[i].z);
        Eigen::Vector3d last_point_a(laserCloudCornerLast->points[closestPointInd].x,
                                     laserCloudCornerLast->points[closestPointInd].y,
                                     laserCloudCornerLast->points[closestPointInd].z);
        Eigen::Vector3d last_point_b(laserCloudCornerLast->points[minPointInd2].x,
                                     laserCloudCornerLast->points[minPointInd2].y,
                                     laserCloudCornerLast->points[minPointInd2].z);

        double s;// 运动补偿系数，kitti数据集的点云已经被补偿过，所以s = 1.0
        if (DISTORTION)
            s = (cornerPointsSharp->points[i].intensity - int(cornerPointsSharp->points[i].intensity)) / SCAN_PERIOD;
        else
            s = 1.0;
        // 用点O，A，B构造点到线的距离的残差项，注意这三个点都是在上一帧的Lidar坐标系下，即，残差 = 点O到直线AB的距离
        // 具体到介绍lidarFactor.cpp时再说明该残差的具体计算方法
        ceres::CostFunction *cost_function = LidarEdgeFactor::Create(curr_point, last_point_a, last_point_b, s);
        problem.AddResidualBlock(cost_function, loss_function, para_q, para_t);
        corner_correspondence++;
    }
}

面特征：

// 下面说的点符号与上述相同
// 与上面的建立corner特征点之间的关联类似，寻找平面特征点O的最近邻点ABC，即基于最近邻原理建立surf特征点之间的关联，find correspondence for plane features
for (int i = 0; i < surfPointsFlatNum; ++i)
{
    TransformToStart(&(surfPointsFlat->points[i]), &pointSel);
    kdtreeSurfLast->nearestKSearch(pointSel, 1, pointSearchInd, pointSearchSqDis);

    int closestPointInd = -1, minPointInd2 = -1, minPointInd3 = -1;
    if (pointSearchSqDis[0] < DISTANCE_SQ_THRESHOLD)// 找到的最近邻点A有效
    {
        closestPointInd = pointSearchInd[0];

        // get closest point's scan ID
        int closestPointScanID = int(laserCloudSurfLast->points[closestPointInd].intensity);
        double minPointSqDis2 = DISTANCE_SQ_THRESHOLD, minPointSqDis3 = DISTANCE_SQ_THRESHOLD;

        // search in the direction of increasing scan line
        for (int j = closestPointInd + 1; j < (int)laserCloudSurfLast->points.size(); ++j)
        {
            // if not in nearby scans, end the loop
            if (int(laserCloudSurfLast->points[j].intensity) > (closestPointScanID + NEARBY_SCAN))
                break;

            double pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) *
                                    (laserCloudSurfLast->points[j].x - pointSel.x) +
                                (laserCloudSurfLast->points[j].y - pointSel.y) *
                                    (laserCloudSurfLast->points[j].y - pointSel.y) +
                                (laserclosestPointScanIDCloudSurfLast->points[j].z - pointSel.z) *
                                    (laserCloudSurfLast->points[j].z - pointSel.z);

            // if in the same or lower scan line
            if (int(laserCloudSurfLast->points[j].intensity) <= closestPointScanID && pointSqDis < minPointSqDis2)
            {
                minPointSqDis2 = pointSqDis;// 找到的第2个最近邻点有效，更新点B，注意如果scanID准确的话，一般点A和点B的scanID相同
                minPointInd2 = j;
            }
            // if in the higher scan line
            else if (int(laserCloudSurfLast->points[j].intensity) > closestPointScanID && pointSqDis < minPointSqDis3)
            {
                minPointSqDis3 = pointSqDis;// 找到的第3个最近邻点有效，更新点C，注意如果scanID准确的话，一般点A和点B的scanID相同,且与点C的scanID不同，与LOAM的paper叙述一致
                minPointInd3 = j;
            }
        }

        // search in the direction of decreasing scan line
        for (int j = closestPointInd - 1; j >= 0; --j)
        {
            // if not in nearby scans, end the loop
            if (int(laserCloudSurfLast->points[j].intensity) < (closestPointScanID - NEARBY_SCAN))
                break;

            double pointSqDis = (laserCloudSurfLast->points[j].x - pointSel.x) *
                                    (laserCloudSurfLast->points[j].x - pointSel.x) +
                                (laserCloudSurfLast->points[j].y - pointSel.y) *
                                    (laserCloudSurfLast->points[j].y - pointSel.y) +
                                (laserCloudSurfLast->points[j].z - pointSel.z) *
                                    (laserCloudSurfLast->points[j].z - pointSel.z);

            // if in the same or higher scan line
            if (int(laserCloudSurfLast->points[j].intensity) >= closestPointScanID && pointSqDis < minPointSqDis2)
            {
                minPointSqDis2 = pointSqDis;
                minPointInd2 = j;
            }
            else if (int(laserCloudSurfLast->points[j].intensity) < closestPointScanID && pointSqDis < minPointSqDis3)
            {
                // find nearer point
                minPointSqDis3 = pointSqDis;
                minPointInd3 = j;
            }
        }

        if (minPointInd2 >= 0 && minPointInd3 >= 0)// 如果三个最近邻点都有效
        {

            Eigen::Vector3d curr_point(surfPointsFlat->points[i].x,
                                        surfPointsFlat->points[i].y,
                                        surfPointsFlat->points[i].z);
            Eigen::Vector3d last_point_a(laserCloudSurfLast->points[closestPointInd].x,
                                            laserCloudSurfLast->points[closestPointInd].y,
                                            laserCloudSurfLast->points[closestPointInd].z);
            Eigen::Vector3d last_point_b(laserCloudSurfLast->points[minPointInd2].x,
                                            laserCloudSurfLast->points[minPointInd2].y,
                                            laserCloudSurfLast->points[minPointInd2].z);
            Eigen::Vector3d last_point_c(laserCloudSurfLast->points[minPointInd3].x,
                                            laserCloudSurfLast->points[minPointInd3].y,
                                            laserCloudSurfLast->points[minPointInd3].z);

            double s;
            if (DISTORTION)
                s = (surfPointsFlat->points[i].intensity - int(surfPointsFlat->points[i].intensity)) / SCAN_PERIOD;
            else
                s = 1.0;
            // 用点O，A，B，C构造点到面的距离的残差注意如果scanID准确的话，一般点A和点B的scanID相注意如果scanID准确的话，一般点A和点B的scanID相项，注意这三个点都是在上一帧的Lidar坐标系下，即，残差 = 点O到平面ABC的距离
            // 同样的，具体到介绍lidarFactor.cpp时再说明该残差的具体计算方法
            ceres::CostFunction *cost_function = LidarPlaneFactor::Create(curr_point, last_point_a, last_point_b, last_point_c, s);
            problem.AddResidualBlock(cost_function, loss_function, para_q, para_t);
            plane_correspondence++;
        }
    }
}

2.2 scan-to-map中特征点匹配

我们通过scan-to-scan获得一个粗位姿之后开始建图，在另一个线程中我们通过scan-to-map的方式获得更加准确的位姿，SLAM最终的精度也就是取决于scan-to-map的精度，而scan-to-scan则可以有IMU或者视觉里程计代替（VLOAM就是这个基本原理）,在scan-to-map中匹配方式主要有以下几点不同

1. 数量不同，在scan-to-map的过程中参与计算的特征点是scan-to-scan的十倍以上；
2. 线特征和面特征获得相邻点的方式不同，在scan-to-scan中是通过直接搜索最近的激光点获得的直线上的两个点或者平面上的三个点，但是在scan-to-map中是搜索最近的5个点，然后通过主成分分析或者最小二乘的方式获得直线和平面的表达式，最后通过采样来获得最后的匹配点，这样做显然会更加鲁棒。

具体代码如下：
线特征

for (int i = 0; i < laserCloudCornerStackNum; i++)
{
    pointOri = laserCloudCornerStack->points[i];
    // 需要注意的是submap中的点云都是world坐标系，而当前帧的点云都是Lidar坐标系，所以
    // 在搜寻最近邻点时，先用预测的Mapping位姿w_curr，将Lidar坐标系下的特征点变换到world坐标系下
    pointAssociateToMap(&pointOri, &pointSel);
    // 在submap的corner特征点（target）中，寻找距离当前帧corner特征点（source）最近的5个点
    kdtreeCornerFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);

    if (pointSearchSqDis[4] < 1.0)
    {
        std::vector<Eigen::Vector3d> nearCorners;
        Eigen::Vector3d center(0, 0, 0);
        for (int j = 0; j < 5; j++)
        {
            Eigen::Vector3d tmp(laserCloudCornerFromMap->points[pointSearchInd[j]].x,
                laserCloudCornerFromMap->points[pointSearchInd[j]].y,
                laserCloudCornerFromMap->points[pointSearchInd[j]].z);
            center = center + tmp;
            nearCorners.push_back(tmp);
        }
        // 计算这个5个最近邻点的中心
        center = center / 5.0;

        // 协方差矩阵
        Eigen::Matrix3d covMat = Eigen::Matrix3d::Zero();
        for (int j = 0; j < 5; j++)
        {
            Eigen::Matrix<double, 3, 1> tmpZeroMean = nearCorners[j] - center;
            covMat = covMat + tmpZeroMean * tmpZeroMean.transpose();
        }

        // 计算协方差矩阵的特征值和特征向量，用于判断这5个点是不是呈线状分布，此为PCA的原理
        Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> saes(covMat);

        // if is indeed line feature
        // note Eigen library sort eigenvalues in increasing order
        Eigen::Vector3d unit_direction = saes.eigenvectors().col(2);// 如果5个点呈线状分布，最大的特征值对应的特征向量就是该线的方向向量
        Eigen::Vector3d curr_point(pointOri.x, pointOri.y, pointOri.z);
        if (saes.eigenvalues()[2] > 3 * saes.eigenvalues()[1])// 如果最大的特征值 >> 其他特征值，则5个点确实呈线状分布，否则认为直线“不够直”
        {
            Eigen::Vector3d point_on_line = center;
            Eigen::Vector3d point_a, point_b;
            // 从中心点沿着方向向量向两端移动0.1m，构造线上的两个点
            point_a = 0.1 * unit_direction + point_on_line;
            point_b = -0.1 * unit_direction + point_on_line;

            // 然后残差函数的形式就跟Odometry一样了，残差距离即点到线的距离，到介绍lidarFactor.cpp时再说明具体计算方法
            ceres::CostFunction* cost_function = LidarEdgeFactor::Create(curr_point, point_a, point_b, 1.0);
            problem.AddResidualBlock(cost_function, loss_function, parameters, parameters + 4);
            corner_num++;
        }
    }
}

面特征：

for (int i = 0; i < laserCloudSurfStackNum; i++)
{
    pointOri = laserCloudSurfStack->points[i];

    pointAssociateToMap(&pointOri, &pointSel);        //也找5个最近邻点
    kdtreeSurfFromMap->nearestKSearch(pointSel, 5, pointSearchInd, pointSearchSqDis);

    // 求面的法向量就不是用的PCA了（虽然论文中说还是PCA），使用的是最小二乘拟合，是为了提效？不确定
    // 假设平面不通过原点，则平面的一般方程为Ax + By + Cz + 1 = 0，用这个假设可以少算一个参数，提效。
    Eigen::Matrix<double, 5, 3> matA0;
    Eigen::Matrix<double, 5, 1> matB0 = -1 * Eigen::Matrix<double, 5, 1>::Ones();
    // 用上面的2个矩阵表示平面方程就是 matA0 * norm（A, B, C） = matB0，这是个超定方程组，因为数据个数超过未知数的个数
    if (pointSearchSqDis[4] < 1.0)
    {
        for (int j = 0; j < 5; j++)
        {
            matA0(j, 0) = laserCloudSurfFromMap->points[pointSearchInd[j]].x;
            matA0(j, 1) = laserCloudSurfFromMap->points[pointSearchInd[j]].y;
            matA0(j, 2) = laserCloudSurfFromMap->points[pointSearchInd[j]].z;
        }
        // 求解这个最小二乘问题，可得平面的法向量，find the norm of plane
        Eigen::Vector3d norm = matA0.colPivHouseholderQr().solve(matB0);
        // Ax + By + Cz + 1 = 0，全部除以法向量的模长，方程依旧成立，而且使得法向量归一化了
        double negative_OA_dot_norm = 1 / norm.norm();
        norm.normalize();

        // Here n(pa, pb, pc) is unit norm of plane
        bool planeValid = true;
        for (int j = 0; j < 5; j++)
        {
            // 点(x0, y0, z0)到平面Ax + By + Cz + D = 0 的距离公式 = fabs(Ax0 + By0 + Cz0 + D) / sqrt(A^2 + B^2 + C^2)
            if (fabs(norm(0) * laserCloudSurfFromMap->points[pointSearchInd[j]].x +
                norm(1) * laserCloudSurfFromMap->points[pointSearchInd[j]].y +
                norm(2) * laserCloudSurfFromMap->points[pointSearchInd[j]].z + negative_OA_dot_norm) > 0.2)
            {
                planeValid = false;// 平面没有拟合好，平面“不够平”
                break;
            }
        }
        Eigen::Vector3d curr_point(pointOri.x, pointOri.y, pointOri.z);
        if (planeValid)
        {
            // 构造点到面的距离残差项，同样的，具体到介绍lidarFactor.cpp时再说明该残差的具体计算方法
            ceres::CostFunction* cost_function = LidarPlaneNormFactor::Create(curr_point, norm, negative_OA_dot_norm);
            problem.AddResidualBlock(cost_function, loss_function, parameters, parameters + 4);
            surf_num++;
        }
    }
}

3. 补充

既然特征点的提取和匹配都已经有了，这里顺带总结下残差优化部分，代码就不贴了，简单记录一下残差优化的公式，首先根据上面特征点匹配过程的我们已经获得了匹配好的线特征和面特征，如下：
对于线特征：

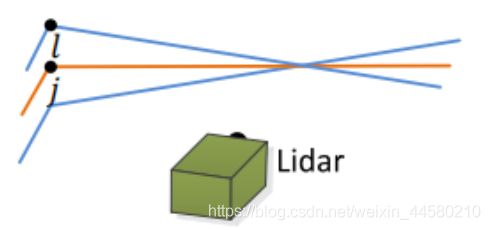
点到直线的距离为：
$$d_{\mathcal{E}}=\frac{\left|\left({\tilde{\mathbf{X}}}_{(k+1,i)}^L-{\overline{\mathbf{X}}}_{(k,j)}^L\right)\times \left({\tilde{\mathbf{X}}}_{(k+1,i)}^L-{\overline{\mathbf{X}}}_{(k,l)}^L\right)\right|}{\left|{\overline{\mathbf{X}}}_{(k,j)}^L-{\overline{\mathbf{X}}}_{(k,l)}^L\right|}$$对于面特征：
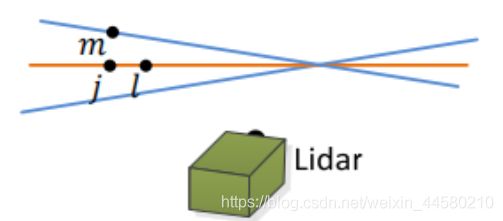
点到平面的距离为：
$$d_{\mathcal{H}}=\frac{\left|\begin{array}{c}\left({\tilde{\mathbf{X}}}_{(k+1,i)}^L-{\overline{\mathbf{X}}}_{(k,j)}^L\right)\\ \left(\left({\overline{\mathbf{X}}}_{(k,j)}^L-{\overline{\mathbf{X}}}_{(k,l)}^L\right)\times \left({\overline{\mathbf{X}}}_{(k,j)}^L-{\overline{\mathbf{X}}}_{(k,m)}^L\right)\right)\end{array}\right|}{\left|\left({\overline{\mathbf{X}}}_{(k,j)}^L-{\overline{\mathbf{X}}}_{(k,l)}^L\right)\times \left({\overline{\mathbf{X}}}_{(k,j)}^L-{\overline{\mathbf{X}}}_{(k,m)}^L\right)\right|}$$那么总的损失计算函数为：
$$\mathrm{loss}=\sum _{i=1}^{N_{\mathcal{E}}}{d}_{\mathcal{E}i}+\sum _{i=1}^{N_{\mathcal{H}}}{d}_{\mathcal{H}i}=D\left({\tilde{\mathbf{X}}}_{k+1,i}^L\right)$$我们需要优化的变量：$${\mathbf{T}}_{k+1}^L={\left[t_x,t_y,t_z,{\theta }_x,{\theta }_y,{\theta }_z\right]}^T$$我们定义：
平移部分为：$$\mathbf{t}={\left[t_x,t_y,t_z\right]}^T$$
旋转部分为：$$\begin{array}{rl}\mathbf{R}& ={\mathbf{R}}_y{\mathbf{R}}_x{\mathbf{R}}_z\\ & =\left[\begin{array}{ccc}{c}_y{c}_z+s_y{s}_x{s}_z& c_z{s}_y{s}_x-c_y{s}_z& c_x{s}_y\\ c_x{s}_z& c_x{c}_z& -s_x\\ c_y{s}_x{s}_z-c_z{s}_y& c_y{c}_z{s}_x+s_y{s}_z& c_y{c}_x\end{array}\right]\end{array}$$其中$$\{\begin{array}{c}{c}_x=\cos \left({\theta }_x\right)\\ s_x=\sin \left({\theta }_x\right)\\ c_y=\cos \left({\theta }_y\right)\\ s_y=\sin \left({\theta }_y\right)\\ c_z=\cos \left({\theta }_z\right)\\ s_z=\sin \left({\theta }_z\right)\end{array}$$我们通过旋转和平移可以将当前帧的激光雷达点投影到目标坐标系下，并在目标坐标系下构建残差，即$${\tilde{\mathbf{X}}}_{(k+1,i)}^L=\mathbf{R}{\mathbf{X}}_{(k+1,i)}^L+\mathbf{t}=G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)$$那么整个过程就可以通过公式表示为：$$\mathrm{loss}=F\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)=D\left(G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)\right)$$假如我们使用列文伯格迭代优化求解优化变量：$${\mathbf{T}}_{k+1}^L\leftarrow {\mathbf{T}}_{k+1}^L-{\left({\mathbf{J}}^T\mathbf{J}+\lambda \mathrm{diag}\left({\mathbf{J}}^{\mathrm{T}}\mathbf{J}\right)\right)}^{-1}{\mathbf{J}}^{\mathrm{T}}\mathbf{d}$$在这个过程中，我们需要求解雅克比矩阵$\mathbf{J}$:$$\begin{array}{rl}\mathbf{J}& =\frac{\partial F\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)}{\partial {\mathbf{T}}_{k+1}^L}\\ & =\frac{\partial D\left(G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)\right)}{\partial {\mathbf{T}}_{k+1}^L}\\ & =\frac{\partial D\left({\tilde{\mathbf{X}}}_{k+1,i}^L\right)}{\partial {\tilde{\mathbf{X}}}_{(k+1,i)}^L}\frac{\partial G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)}{\partial {\mathbf{T}}_{k+1}^L}\end{array}$$对于线特征, 梯度方向为通过特征点的垂直于直线的方向，因此前一项有：$$\frac{\partial D\left({\tilde{\mathbf{X}}}_{k+1,i}^L\right)}{\partial {\tilde{\mathbf{X}}}_{(k+1,i)}^L}={\left[a_{\mathcal{E}},b_{\mathcal{E}},c_{\mathcal{E}}\right]}^T$$对于面特征, 梯度方向为通过特征点的垂直于平面的方向，因此前一项有：$$\frac{\partial D\left({\tilde{\mathbf{X}}}_{k+1,i}^L\right)}{\partial {\tilde{\mathbf{X}}}_{(k+1,i)}^L}={\left[a_{\mathcal{H}},b_{\mathcal{H}},c_{\mathcal{H}}\right]}^T$$对于后一项，对于平移求导有：$$\begin{array}{rl}& \frac{\partial G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)}{\partial {\mathbf{t}}_x}\\ =& \frac{\partial G\left(\mathbf{R}{\mathbf{X}}_{(k+1,i)}^L+\mathbf{t}\right)}{\partial {\mathbf{t}}_x}\\ =& \left[\begin{array}{l}1\\ 0\\ 0\end{array}\right]\end{array}$$同理可以推到其他两项，对于旋转求导有：$$\begin{array}{rl}& \frac{\partial G\left({\mathbf{X}}_{(k+1,i)}^L,{\mathbf{T}}_{k+1}^L\right)}{\partial {\mathbf{\theta }}_x}\\ =& \frac{\partial G\left(\mathbf{R}{\mathbf{X}}_{(k+1,i)}^L+\mathbf{t}\right)}{\partial {\mathbf{\theta }}_x}\\ =& \frac{\partial G\left(\mathbf{R}{\mathbf{X}}_{(k+1,i)}^L\right)}{\partial {\mathbf{\theta }}_x}\\ =& \left[\begin{array}{ccc}{s}_y{c}_x{s}_z& c_z{s}_y{c}_x& -s_x{s}_y\\ -s_x{s}_z& -s_x{c}_z& -c_x\\ c_y{c}_x{s}_z& c_y{c}_z{c}_x& -c_y{s}_x\end{array}\right]\left[\begin{array}{c}{x}_{(k+1,i)}\\ y_{(k+1,i)}\\ z_{(k+1,i)}\end{array}\right]\end{array}$$同理可以推到其他两项

以上就完成了全部的推导过程，这里值得注意的是，在LOAM中旋转是针对欧拉角求导的，这是很原始的表达方式了。

那么到此就完成了整片博客的内容，了解了这些内容，LOAM算法的基本原理就可以算了解了，剩下的就是一些实现过程中的细节，例如如何维护局部地图等，之后实践的过程中再去慢慢理解，有问题欢迎交流～

此外，对其他SLAM算法感兴趣的同学可以看考我的博客SLAM算法总结——经典SLAM算法框架总结