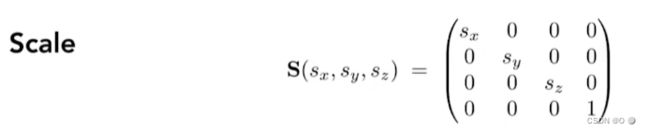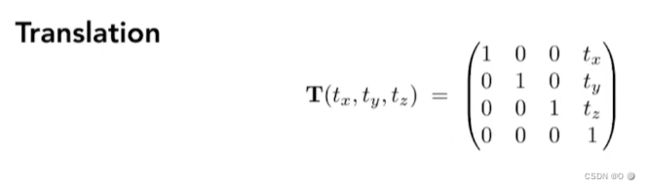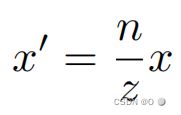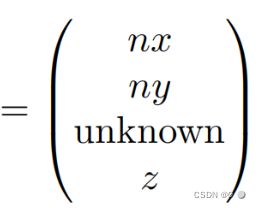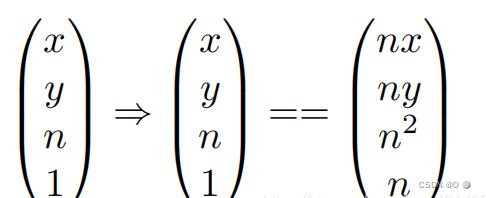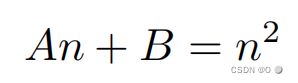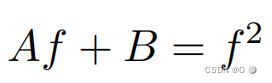【计算机图形学01】坐标变换
-
坐标系统
将坐标变换为标准化设备坐标,接着再转化为屏幕坐标的过程通常是分步进行的,也就是类似于流水线那样子。在流水线中,物体的顶点在最终转化为屏幕坐标之前还会被变换到多个坐标系统(Coordinate System)。将物体的坐标变换到几个过渡坐标系(Intermediate Coordinate System)的优点在于,在这些特定的坐标系统中,一些操作或运算更加方便和容易,这一点很快就会变得很明显。对我们来说比较重要的总共有5个不同的坐标系统
局部坐标系->模型矩阵变换->世界坐标系->视图矩阵变换->相机坐标系->投影矩阵->裁剪坐标系->视口变换->屏幕坐标
-
局部空间坐标系/物体空间坐标系/模型空间坐标系
局部空间是指物体所在的坐标空间,即对象最开始所在的地方.
-
局部模型矩阵变换
子模型矩阵的缩放S,平移T,旋转R矩阵。(先做缩放线性变换再平移旋转)
缩放矩阵
平移矩阵
旋转矩阵
绕X轴旋转
绕Y轴旋转
绕Z轴旋转
-
世界空间坐标系
一旦对物体进行了建模,下一步就是将各个对象或者图形组合放到我们希望绘制的平面场景中。如上所述,每一个对象在创建时都有自身的建模坐标系,当我们将其组合放置在一起时,为了确定每一个对象的位置及其他对象的相对位置,就必须抛弃每一个对象自身的坐标系,将其纳入到一个统一的坐标系中,这个坐标系称为世界坐标系,也称用户坐标系,它是一个全局坐标系,也是一个典型的平面直角坐标系。这个过程实质上是将一个物体从局部空间组合装配到世界空间的变换过程。
-
视图变换矩阵
-
视图矩阵
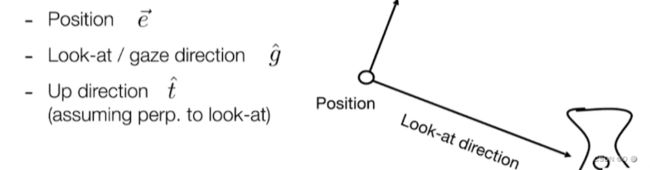
原点为e向量
看物体的方向g向量
向上看的t向量
把摄像机(观察者)坐标系变换到原点
具体矩阵R为正交矩阵所以R的逆矩阵=R的转置矩阵
在模型矩阵中,我们关心的是空间中的点在经历变换后在世界坐标系下的位置。事实上,我们更加关心空间中的点相对于观察者的位置。最简单的方案是将观察者置于原点处,面向z轴(或x轴、y轴)正半轴,那么空间中的点在世界坐标系下的位置就是其相对于观察者的位置。
观察者的位置和方向会变化,看上去就好像整个世界的位置和方向发生变化了一样,所以解决的方案很简单,将世界里的所有模型看作一个大模型,在所有模型矩阵的左侧再乘以一个表示整个世界变换的模型矩阵,就可以了。这个表示整个世界变换的矩阵又称为“视图矩阵”,因为他们经常一起工作,所以将视图矩阵乘以模型矩阵得到的矩阵称为“模型视图矩阵”。模型视图矩阵的作用是:乘以一个点坐标,获得一个新的点坐标,获得的点坐标表示点在世界里变换,同时观察者也变换位置,观察者也变换后,点相对于观察者的位置。视图矩阵同样也可以分为平移、旋转和缩放,视图矩阵是将观察者视为一个模型,获得的观察者在世界中变换的模型矩阵的逆矩阵(这里可以看成观察者不移动,但是世界相对观察者运动)。
相机平移了(tx,ty,tz),视图矩阵如下,可以看出如果将视图矩阵看作整个世界的模型矩阵,相当于整个世界平移了(-tx,-ty,-tz)。
相机绕z轴旋转了角度θ,视图矩阵如下,相当于整个世界绕z轴旋转了-θ度。
相机在三个方向等比例缩小了s倍,视图矩阵如下,相当于整个世界放大了s倍。
一个模型可能由多个较小的子模型组成,模型自身有其模型矩阵,而子模型也有自己的局部模型矩阵
-
观察空间坐标系/视觉空间坐标系/相机空间坐标系
观察空间经常被人们称之OpenGL的摄像机(Camera)(所以有时也称为摄像机空间(Camera Space)或视觉空间(Eye Space))。观察空间是将世界空间坐标转化为用户视野前方的坐标而产生的结果。因此观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成,平移/旋转场景从而使得特定的对象被变换到摄像机的前方。
-
投影矩阵
正交投影
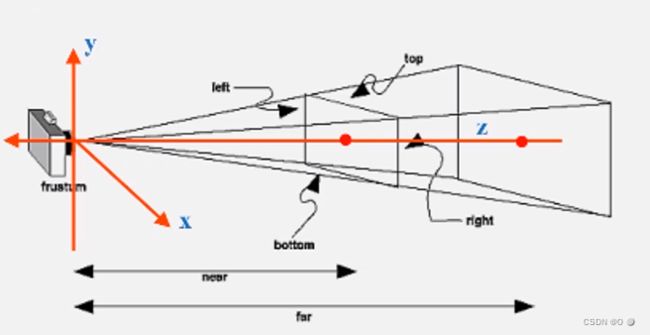
正交投影就是摄像机在原点,看向-z方向,顶部在y方向,在看向物体时将所有物体的z值归0,然后将物体平移并缩放到[-1,1]^2之间。
[左,右],[下,上],[远,近] 把模型正交投影到世界坐标下的正方体上
透视投影
简而言之,透视投影就是近大远小,平行线也会变得不平行,人们眼睛所看到的就是透视投影的结果。
空间上为圆锥:
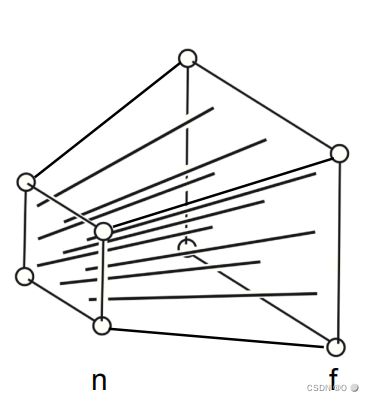
摄像机为坐标轴的放射出一个四棱锥中的点上的近平面与远平面的空间图:
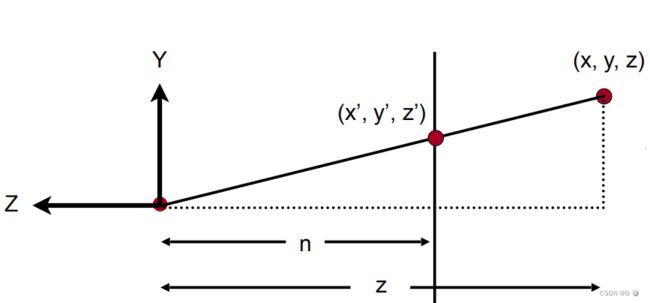
二维图:
远近平面形成两个三角形,且这两个三角形互为相似三角形
故:
同理
在其次坐标系中近平面上的向量可以写作:
近平面的向量写作矩阵形式为:
由于任何在近平面上的点是不会变的。
任何在远平面的点的z值也不会变。
故:
由于其他三行的值都已知,所以现在只用算第三行的值。又因为由近平面得出的第三行为n^2,所以可确定透视变正交矩阵第三行的前两维为0,所以可得:
可得:
同理远平面
联立连个方程可得:
求出投影矩阵的压缩矩阵
透视投影矩阵就等于正交投影矩阵乘以透视变正交矩阵
在一个顶点着色器运行的最后,OpenGL期望所有的坐标都能落在一个特定的范围内,且任何在这个范围之外的点都应该被裁剪掉(Clipped)。被裁剪掉的坐标就会被忽略,所以剩下的坐标就将变为屏幕上可见的片段。这也就是裁剪空间(Clip Space)名字的由来。
-
视口变换
在我们做完投影变换后所有物体都映射在标准坐标系中,但是屏幕会有各种各样的分辨率,所以视口变换是为了将正常设备坐标映射到屏幕坐标。
假设屏幕的宽为width,高度为height,那么视口变换就是把[-1,1]^2的xy平面变到[0,width]x[0,height],这里为什么没有考虑z轴的变换是因为z轴在之后的其他地方有用。
根据上述可得出视口变换矩阵为:
-
屏幕空间坐标系/设备坐标系统