深度学习基础 - 单位向量
深度学习基础 - 单位向量
flyfish
有向线段-》向量-》向量放到坐标轴里-》计算向量的长度-》单位向量-》三角函数表示向量的分量
空间中的向量
有向线段 A B {AB} AB有起点A和终点B；加上箭头就是向量 A B ⃗ \vec{AB} AB，或者 v ⃗ \vec{v} v,或者 a ⃗ \vec{a} a
将向量放到坐标轴里，A和B这两个点都有各自的坐标
A = ( 1 , 2 ) A=(1, 2) A=(1,2)
B = ( 5 , 6 ) B = (5, 6) B=(5,6)
如果平面上的一个向量 v ⃗ \vec{v} v等于起点在原点 ( 0 , 0 ) (0,0) (0,0),终点在 ( v 1 , v 2 ) (v_1,v_2) (v1,v2)的向量,则向量 v ⃗ \vec{v} v的分量形式是 v ⃗ = < v 1 , v 2 > \vec{v}=
这样一个平面向量也就是实数的有序对 < v 1 , v 2 >
向量的长度也叫向量的模
∣ v ⃗ ∣ = ( v 1 ) 2 + ( v 2 ) 2 = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 \begin {aligned} |\vec{v}|=\sqrt{(v_1)^2+(v_2)^2} =\sqrt{(x_2-x_1)^2+(y_2- y_1)^2} \end {aligned} ∣v∣=(v1)2+(v2)2=(x2−x1)2+(y2−y1)2
或者说2范数
∥ X ∥ 2 : = x 1 2 + ⋯ + x n 2 . \begin {aligned} {\displaystyle \left\|{ {X}}\right\|_{2}:={\sqrt {x_{1}^{2}+\cdots +x_{n}^{2}}}.} \end {aligned} ∥X∥2:=x12+⋯+xn2.
假如向量是 v ⃗ = ( v 1 , v 2 ) \vec{v}=\left(v_{1}, v_{2}\right) v=(v1,v2) 那么计算向量长度的方法是
∥ v ⃗ ∥ = v 1 2 + v 2 2 \|\vec{v}\|=\sqrt{v_{1}^{2}+v_{2}^{2}} ∥v∥=v12+v22
举例说明 v ⃗ = ( 4 , 2 ) \vec{v}=(4,2) v=(4,2).
v 1 = 4 v_{1}=4 v1=4 和 v 2 = 2 v_{2}=2 v2=2 计算过程是
∥ v ⃗ ∥ = 4 2 + 2 2 = 20 = 2 5 \|\vec{v}\|=\sqrt{4^{2}+2^{2}}=\sqrt{20}=2 \sqrt{5} ∥v∥=42+22=20=25
双竖线与数的绝对值区分
单位向量
单位向量（Unit Vector）就是长度为1的向量
有了单位向量就可以度量其他向量
这里的符号是小写的字母a的头上再戴一顶帽子，读作 a hat
比例
向量a相当于单位向量2.5倍，方向仍然不变
任何平面向量 v ⃗ = < a , b > \vec{v}=
线性组合
v ⃗ = < a , b > = < a , 0 > + < 0 , b > = a < 1 , 0 > + b < 0 , 1 > = a i + b j \begin {aligned} \vec{v}&=
假如有这样的向量
v ⃗ = [ 2 1 ] \vec{v}=\begin{bmatrix} 2 \\\\ 1 \end{bmatrix} v=⎣ ⎡21⎦ ⎤
用图表示
向量是有大小和方向的， 图中的magnitude表示有多长
一维的单位向量通常写 i i i
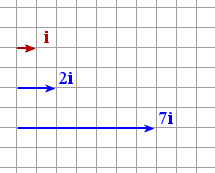
图中红色的是单位向量，标记为 i i i。
用单位向量表示另外两个向量分别是 2 i 2i 2i 和 7 i 7i 7i
二维的单位向量
x x x 方向的一个单位向量 i i i和 y y y 方向的一个单位向量 j j j。
可以用单位向量 i i i 和 j j j 表示出任意二维向量。下图可以通过数方格的个数，看大小.
可以这样写出向量的分量
V x = 6 i V_x =6i Vx=6i
V y = 3 j V_y =3j Vy=3j
用单位向量表示出向量V$
V = 6 i + 3 j V= 6i+3j V=6i+3j
向量a相当于 在x轴移动2个“x”的单位向量
和在y轴移动1.3个“y”的单位向量
v = 2 i − 0.5 j = 2 [ 1 0 ] − 0.5 [ 0 1 ] = [ 2 ⋅ 1 2 ⋅ 0 ] − [ 0.5 ⋅ 0 0.5 ⋅ 1 ] = [ 2 − 0.5 ] \begin{aligned} \\ v &= 2i - 0.5j \\\\ &= 2\begin{bmatrix} 1 \\\\ 0 \end{bmatrix} - 0.5\begin{bmatrix} 0 \\\\ 1 \end{bmatrix} \\\\ &= \begin{bmatrix} 2 \cdot 1 \\\\ 2 \cdot 0 \end{bmatrix} - \begin{bmatrix} 0.5 \cdot 0 \\\\ 0.5 \cdot 1 \end{bmatrix} \\\\ &= \begin{bmatrix} 2 \\\\ -0.5 \end{bmatrix} \end{aligned} v=2i−0.5j=2⎣ ⎡10⎦ ⎤−0.5⎣ ⎡01⎦ ⎤=⎣ ⎡2⋅12⋅0⎦ ⎤−⎣ ⎡0.5⋅00.5⋅1⎦ ⎤=⎣ ⎡2−0.5⎦ ⎤
一维的情况下，单位向量 i i i 也就是向量的基底 i {i} i,也叫坐标向量
二维的情况下，单位向量 i , j i,j i,j 也就是向量的基底 i , j {i,j} i,j
三维的情况下，单位向量 i , j , k i,j,k i,j,k 也就是向量的基底 i , j , k {i,j,k} i,j,k
坐标轴上以原点为圆心，以 1 为半径画一个圆
蓝色和红色都是单位向量，蓝色为标准单位向量
若 v ⃗ = < v 1 , v 2 > \vec{v}=
单位向量 ∣ v ⃗ ∣ = 1 \left | \vec{v} \right | =1 ∣v∣=1
v 1 = ∣ v ∣ cos θ = cos θ v1=\left | v \right | \cos \theta =\cos \theta v1=∣v∣cosθ=cosθ
v 2 = ∣ v ∣ sin θ = sin θ v2=\left | v \right | \sin \theta =\sin \theta v2=∣v∣sinθ=sinθ
与正 x x x轴形成角 θ \theta θ 的单位向量v表示为
v ⃗ = < cos θ , sin θ > \vec{v}=<\cos \theta,\sin \theta> v=<cosθ,sinθ>