宋浩概率论与数理统计笔记——第一章
大二记的笔记,现在拿出来和大家分享下
引言
确定性(必然)现象:一定发生(不发生)
随机(偶然)现象:可能发生、可能不发生
统计规律
1.1.1随机试验与随机事件
试验:观察、测量、实验
随机试验:
1. 在相同条件下可重复
2. 结果不止一个
3. 无法预测
事件:试验的每种结果
随机事件
基本事件:相对于实验目的来说不能再分(不必在分)
复合事件:由基本事件复合
必然事件:一定发生 Ω
不可能事件:一定不发生 Φ
1.1.2样本空间与事件的集合表示
样本空间:所有基本事件的集合 Ω
样本点:样本空间中的元素 ω
例:扔两个硬币,他的样本空间 Ω={(正,正)(正,反)(反,反)(反,正)}
例:
在[a,b]区间内扔一个质子 坐标 Ω=[a,b]
向平面扔一个质子 Ω={(x,y)|x,y∈R}
向空间扔一个质子 Ω={(x,y,z)|x,y,z∈R}
事件的集合表示:扔骰子点数小于3 C={1,2}
Ω——必然事件——样本空间
Φ——不可能事件——空集
事件——Ω的子集
1.1.3事件间的关系
(1)包含:A发生必然导致B发生 A ⊂ B {A\sub B} A⊂B
ϕ ⊂ A ⊂ Ω \phi\sub A \sub \Omega ϕ⊂A⊂Ω
(2)并(和)A与B中至少一个发生 A ⋃ B A\bigcup B A⋃B
(3)交(积)A、B同时发生 A ⋂ B A\bigcap B A⋂B
无限可列个:按某种规律排成一个序列
①自然数:0,1,2,3,…
②整数:0,1,-1,2,-2,…
③有理数: p q \frac{p}{q} qp:0, 1 1 \frac{1}{1} 11, − 1 1 \frac{-1}{1} 1−1, 1 2 \frac{1}{2} 21, − 1 2 \frac{-1}{2} 2−1,…
0.56565656... = x 0.56565656...=x 0.56565656...=x
56.56565656... = 100 x 56.56565656...=100x 56.56565656...=100x
56 = 100 x − x = 99 x 56=100x-x=99x 56=100x−x=99x
x = 56 99 x=\frac{56}{99} x=9956
0.1 2 ˙ = 0.1 + 0.0 2 ˙ = 1 10 + 2 90 = 11 90 0.1\dot2=0.1+0.0\dot2=\frac{1}{10}+\frac{2}{90}=\frac{11}{90} 0.12˙=0.1+0.02˙=101+902=9011
①实数②直线点集
(4)差A-B
(5)互不相容事件
A、B不同时发生 AB= ϕ \phi ϕ
n个事件 A 1 , A 2 , A 3 , . . . , A n A_1,A_2,A_3,...,A_n A1,A2,A3,...,An 若有 A i A j = ϕ A_iA_j=\phi AiAj=ϕ则这些事件两两互不相容
(6)对立事件:A、B互不相容,且 A ⋃ B = Ω A\bigcup B=\Omega A⋃B=Ω
A = B ˉ A=\bar B A=Bˉ B = A ˉ B=\bar A B=Aˉ
1) A ˉ \bar A Aˉ是A的逆 A ˉ ˉ = A \bar{\bar{A}}=A Aˉˉ=A
2) A − B = A − A B = A B ˉ A-B=A-AB=A\bar B A−B=A−AB=ABˉ
互不相容事件和对立事件的联系与区别
1)两事件对立,则一定是互不相容的
2)互不相容适用于多个事件
对立只适用于两个事件
3)互不相容表示不能同时发生,也可以都不发生
对立是有且只有一个
(7)完备事件组
A 1 , A 2 , A 3 , . . . , A n A_1,A_2,A_3,...,A_n A1,A2,A3,...,An两两互不相容且 ⋃ i = 1 n A i = Ω \bigcup_{i=1}^{n}A_i=\Omega ⋃i=1nAi=Ω
运算律
1)交换律
A ⋃ B = B ⋃ A A\bigcup B=B\bigcup A A⋃B=B⋃A A ⋂ B = B ⋂ A A\bigcap B=B\bigcap A A⋂B=B⋂A
2)结合律
( A ⋃ B ) ⋃ C = A ⋃ ( B ⋃ C ) (A\bigcup B)\bigcup C=A\bigcup(B\bigcup C) (A⋃B)⋃C=A⋃(B⋃C)
( A ⋂ B ) ⋂ C = A ⋂ ( B ⋂ C ) (A\bigcap B)\bigcap C=A\bigcap(B\bigcap C) (A⋂B)⋂C=A⋂(B⋂C)
3)分配律
( A ⋃ B ) ⋂ C = ( A ⋂ C ) ⋃ ( B ⋂ C ) (A\bigcup B)\bigcap C=(A\bigcap C)\bigcup(B\bigcap C) (A⋃B)⋂C=(A⋂C)⋃(B⋂C)
( A ⋂ B ) ⋃ C = ( A ⋃ C ) ⋂ ( B ⋃ C ) (A\bigcap B)\bigcup C=(A\bigcup C)\bigcap(B\bigcup C) (A⋂B)⋃C=(A⋃C)⋂(B⋃C)
4)对偶律
A ⋃ B ‾ = A ‾ ⋂ B ‾ \overline{A \bigcup B}= \overline A \bigcap \overline B A⋃B=A⋂B
A ⋂ B ‾ = A ‾ ⋃ B ‾ \overline{A\bigcap B}= \overline A \bigcup \overline B A⋂B=A⋃B
A 1 ⋃ A 2 ⋃ . . . ⋃ A n ‾ = A ‾ 1 ⋂ A ‾ 2 ⋂ . . . ⋂ A ‾ n \overline{A_1\bigcup A_2\bigcup ...\bigcup A_n}= \overline A_1 \bigcap \overline A_2 \bigcap ...\bigcap \overline A_n A1⋃A2⋃...⋃An=A1⋂A2⋂...⋂An
A 1 ⋂ A 2 ⋂ . . . ⋂ A n ‾ = A ‾ 1 ⋃ A ‾ 2 ⋃ . . . ⋃ A ‾ n \overline{A_1\bigcap A_2\bigcap ...\bigcap A_n}= \overline A_1 \bigcup \overline A_2 \bigcup ...\bigcup \overline A_n A1⋂A2⋂...⋂An=A1⋃A2⋃...⋃An
例:射击打3枪 A i , i = 1 , 2 , 3 A_i,i=1,2,3 Ai,i=1,2,3,第 i i i次击中
-
A 1 + A 2 A_1+A_2 A1+A2:前两次至少击中一次
-
A ‾ 2 \overline A_2 A2:第二次未击中
-
A 1 + A 2 + A 3 A_1+A_2+A_3 A1+A2+A3:三次至少击中一次
-
A 1 A 2 A 3 A_1A_2A_3 A1A2A3:三次全中
-
A 2 − A 3 = A 2 A ‾ 3 A_2-A_3=A_2\overline A_3 A2−A3=A2A3:第二次中,第三次未中
-
A 1 + A 3 ‾ = A 1 ‾ ⋂ A 3 ‾ \overline {A_1+A_3}=\overline{A_1}\bigcap \overline{A_3} A1+A3=A1⋂A3:第一、三次未中
-
A 1 ‾ + A 3 ‾ \overline{A_1}+\overline{A_3} A1+A3:第一、三次至少一次未中
1.2.1概率的初等描述
概率:发生可能性的大小P(A)
性质:
- P( Ω \Omega Ω)=1,P( ϕ \phi ϕ)=0
- 0 ⩽ P ( A ) ⩽ 1 0\leqslant P(A)\leqslant 1 0⩽P(A)⩽1
1.2.2古典概率模型
条件:
-
有限个样本点
-
等可能性
P(A)= A 的 有 利 样 本 点 Ω 中 样 本 点 总 数 = A 中 包 含 的 基 本 事 件 数 基 本 事 件 总 数 \frac{A的有利样本点}{ \Omega中样本点总数}=\frac{A中包含的基本事件数}{基本事件总数} Ω中样本点总数A的有利样本点=基本事件总数A中包含的基本事件数
排列组合
加法原理
乘法原理
排列
- 不重复排列(从n个元素中取出m个排列)
P n m = n ( n − 1 ) ( n − 1 ) . . . ( n − m + 1 ) = n ! ( n − m ) ! P_n^m=n(n-1)(n-1)...(n-m+1)=\frac{n!}{(n-m)!} Pnm=n(n−1)(n−1)...(n−m+1)=(n−m)!n!
全排列
P n n = n ! P_n^n=n! Pnn=n!
0!=1
①1!=1×0!
② P 0 0 = 0 ! = 1 P_0^0=0!=1 P00=0!=1 从0个里选0个,只有一种情况
③ P n n = n ! ( n − n ) ! = n ! 0 ! = n ! P_n^n=\frac{n!}{(n-n)!}=\frac{n!}{0!}=n! Pnn=(n−n)!n!=0!n!=n!
- 重复排列(从n个不同的元素中去m个排列)
n × n × n × . . . × n = n m n\times n\times n\times ...\times n=n^m n×n×n×...×n=nm
组合:从n个不同的元素中取出m个不同的元素
C n m = P n m m ! = n ! m ! ( n − m ) ! C_n^m=\frac{P_n^m}{m!}=\frac{n!}{m!(n-m)!} Cnm=m!Pnm=m!(n−m)!n!
C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m C n 0 = C n n = 1 C_n^0=C_n^n=1 Cn0=Cnn=1
例:一套五卷的选集,放书架上,求自左向右或自右向左是1,2,3,4,5的概率
2 P 5 5 = 1 60 \frac{2}{P_5^5}=\frac{1}{60} P552=601
例:4个邮筒,2封信
-
前两个邮筒各投入一封信的概率
P 2 2 4 × 4 = 1 8 \frac{P_2^2}{4\times 4}=\frac{1}{8} 4×4P22=81
-
第二个邮筒恰有一封信
C 2 1 C 3 1 4 × 4 = 3 8 \frac{C_2^1C_3^1}{4\times4}=\frac{3}{8} 4×4C21C31=83
3.两封信投入不同邮筒
4 × 3 16 \frac{4\times3}{16} 164×3
1 − 4 16 1-\frac{4}{16} 1−164
例:5白球4黑球,任取三个球
-
2白1黑
C 5 2 C 4 1 C 9 3 \frac{C_5^2C_4^1}{C_9^3} C93C52C41
-
没黑球
C 5 3 C 9 3 \frac{C_5^3}{C_9^3} C93C53
-
颜色相同
C 5 3 + C 4 3 C 9 3 \frac{C_5^3+C_4^3}{C_9^3} C93C53+C43, 1 − C 5 2 C 4 1 C 9 3 − C 5 1 C 4 2 C 9 3 1-\frac{C_5^2C_4^1}{C_9^3}-\frac{C_5^1C_4^2}{C_9^3} 1−C93C52C41−C93C51C42
例:a个白,b个黑,任取一个为白球的概率
a a + b \frac{a}{a+b} a+ba
例:a个白,b个黑,接连取出m个球(1<=m<=a+b),第m次是白球的概率
法1: a ( a + b − 1 ) ! ( a + b ) ! = a a + b \frac{a(a+b-1)!}{(a+b)!}=\frac{a}{a+b} (a+b)!a(a+b−1)!=a+ba
法2: a × P a + b − 1 m − 1 P a + b m = a a + b \frac{a\times P_{a+b-1}^{m-1}}{P^{m}_{a+b}}=\frac{a}{a+b} Pa+bma×Pa+b−1m−1=a+ba
法3: a a + b \frac{a}{a+b} a+ba
古典性质:
- 非负性, 0 ⩽ P ( A ) ⩽ 1 0\leqslant P(A)\leqslant 1 0⩽P(A)⩽1
- 规范性,P( Ω \Omega Ω)=1,P( ϕ \phi ϕ)=0
- 有限可加 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An互不相容
P ( A 1 + A 2 + . . . + A n ) = P ( A 1 ) + P ( A 2 ) + . . . + P ( A n ) P(A_1+A_2+...+A_n)=P(A_1)+P(A_2)+...+P(A_n) P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)
缺点:必须是有限个结果,结果是等可能性
1.2.3几何概型
线段、平面、立体
例:会面问题
甲乙两人,6:00-7:00 先到者等一刻钟,甲乙两人在一小时内任一时刻都可到达
A——两人见面,x——甲到达时间,y——乙到达时间
蒲丰投针:
在平面上画有等距离为2a(a>0)的一些平行线,向平面上随机投一长2L(L
解:
A——平行线与针相交
x——针的中心距离最近一条直线的距离, θ \theta θ——针与平行线正方向的夹角
0 ≤ x ≤ a 0\leq x\leq a 0≤x≤a ,$0 \leq \theta \leq \pi $
试验的样本空间 Ω = [ 0 , a ] × [ 0 , π ] \Omega=[0,a]\times[0,\pi] Ω=[0,a]×[0,π]
A = x ≤ s i n θ , 0 ≤ θ ≤ π A={x\leq sin\theta,0\leq \theta \leq \pi} A=x≤sinθ,0≤θ≤π
S ( A ) = ∫ 0 π l s i n θ d θ = 2 l S(A)=\int_0^\pi lsin\theta d\theta=2l S(A)=∫0πlsinθdθ=2l
P ( A ) = S ( A ) S ( Ω ) = 2 l a π P(A)=\frac{S(A)}{S(\Omega)}=\frac{2l}{aπ} P(A)=S(Ω)S(A)=aπ2l
完全可加性:
两两互不相容
P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty}A_i)=\sum_{i=1}^{\infty}P(A_i) P(⋃i=1∞Ai)=∑i=1∞P(Ai)
蒙特卡罗方法(统计模拟方法)
1.2.4频率与概率
做n次试验,A发生了m次, m n \frac{m}{n} nm就是频率
记作: ω n ( A ) \omega_n(A) ωn(A)
性质
- 非负性 0 ≤ ω n ( A ) ≤ 1 0\leq \omega_n(A) \leq 1 0≤ωn(A)≤1
- 规范性 ω n ( Ω ) = 1 , ω n ( ϕ ) = 0 \omega_n(\Omega)=1,\omega_n(\phi)=0 ωn(Ω)=1,ωn(ϕ)=0
- 可加性, A 1 , A 2 , . . . , A m A_1,A_2,...,A_m A1,A2,...,Am互不相容
ω n ( A 1 + . . . + A m ) = ω n ( A 1 ) + . . . + ω n ( A m ) \omega_n(A_1+...+A_m)=\omega_n(A_1)+...+\omega_n(A_m) ωn(A1+...+Am)=ωn(A1)+...+ωn(Am)
1.2.5公理化
公理1(非负) 0 ≤ P ( A ) ≤ 1 0\leq P(A) \leq1 0≤P(A)≤1
公理2(规范) P ( Ω ) = 1 P(\Omega)=1 P(Ω)=1
公理3(完全可加) A 1 , A 2 , . . . 不 相 容 A_1,A_2,...不相容 A1,A2,...不相容
P ( A 1 + A 2 + . . . ) = P ( A 1 ) + P ( A 2 ) + . . . P(A_1+A_2+...)=P(A_1)+P(A_2)+... P(A1+A2+...)=P(A1)+P(A2)+...
性质一: P ( ϕ ) = 0 P(\phi)=0 P(ϕ)=0
证:
Ω = Ω + ϕ + ϕ + . . . \Omega=\Omega+\phi+\phi+... Ω=Ω+ϕ+ϕ+...
P ( Ω ) = P ( Ω + ϕ + ϕ + . . . ) = P ( Ω ) + P ( ϕ ) + P ( ϕ ) + . . . P(\Omega)=P(\Omega+\phi+\phi+...)=P(\Omega)+P(\phi)+P(\phi)+... P(Ω)=P(Ω+ϕ+ϕ+...)=P(Ω)+P(ϕ)+P(ϕ)+...
P ( ϕ ) + P ( ϕ ) + . . . = 0 P(\phi)+P(\phi)+...=0 P(ϕ)+P(ϕ)+...=0
又 ∵ P ( ϕ ) ≥ 0 \because P(\phi) \geq 0 ∵P(ϕ)≥0
∴ P ( ϕ ) = 0 \therefore P(\phi) = 0 ∴P(ϕ)=0
性质二:有限可加, A 1 , A 2 , . . . 不 相 容 A_1,A_2,...不相容 A1,A2,...不相容
P ( A 1 + A 2 + . . . A n ) = P ( A 1 ) + P ( A 2 ) + . . . + P ( A n ) P(A_1+A_2+...A_n)=P(A_1)+P(A_2)+...+P(A_n) P(A1+A2+...An)=P(A1)+P(A2)+...+P(An)
证:
A 1 , . . . , A n , ϕ , ϕ , . . . A_1,...,A_n,\phi,\phi,... A1,...,An,ϕ,ϕ,...不相容
P ( A 1 + . . . A n ) = P ( A 1 + . . . + A n + ϕ + ϕ + . . . ) = P ( A 1 ) + . . . + P ( A n ) + P ( ϕ ) + P ( ϕ ) + . . . P(A_1+...A_n)=P(A_1+...+A_n+\phi+\phi+...)=P(A_1)+...+P(A_n)+P(\phi)+P(\phi)+... P(A1+...An)=P(A1+...+An+ϕ+ϕ+...)=P(A1)+...+P(An)+P(ϕ)+P(ϕ)+...
性质三:
P ( A ˉ ) = 1 − P ( A ) P(\bar A)=1-P(A) P(Aˉ)=1−P(A)
证:
A ⋂ A ˉ = ϕ A\bigcap \bar A=\phi A⋂Aˉ=ϕ, A + A ˉ = Ω A+\bar A=\Omega A+Aˉ=Ω
P ( Ω ) = P ( A + A ˉ ) = P ( A ) + P ( A ˉ ) = 1 P(\Omega)=P(A+\bar A)=P(A)+P(\bar A)=1 P(Ω)=P(A+Aˉ)=P(A)+P(Aˉ)=1
推论:
A 1 , . . . , A n A_1,...,A_n A1,...,An完备事件组 { 两 两 不 相 容 并 是 Ω , P ( A 1 ) + . . . + P ( A n ) = 1 \begin{cases} 两两不相容\\并是\Omega, P(A_1)+...+P(A_n)=1 \end{cases} {两两不相容并是Ω,P(A1)+...+P(An)=1
P ( Ω ) = P ( A 1 + . . . A n ) = P ( A 1 ) + . . . + P ( A n ) = 1 P(\Omega)=P(A_1+...A_n)=P(A_1)+...+P(A_n)=1 P(Ω)=P(A1+...An)=P(A1)+...+P(An)=1
性质四:
① P ( A − B ) = P ( A ) − P ( A B ) P(A-B)=P(A)-P(AB) P(A−B)=P(A)−P(AB)
② A ⊃ B , P ( A − B ) = P ( A ) − P ( B ) 且 P ( A ) ≥ P ( B ) A\supset B,P(A-B)=P(A)-P(B)且P(A)\geq P(B) A⊃B,P(A−B)=P(A)−P(B)且P(A)≥P(B)
证:
① A = ( A − B ) ⋃ A B A=(A-B)\bigcup AB A=(A−B)⋃AB, A − B 与 A B 互 不 相 容 A-B与AB互不相容 A−B与AB互不相容
$P(A)=P(A-B)+P(AB) $
$P(A-B)=P(A)-P(AB) $
② ∵ A ⊃ B \because A \supset B ∵A⊃B
∴ P ( A B ) = P ( B ) \therefore P(AB)=P(B) ∴P(AB)=P(B)
∴ P ( A − B ) = P ( A ) − P ( B ) \therefore P(A-B)=P(A)-P(B) ∴P(A−B)=P(A)−P(B)
∵ P ( A − B ) ≥ 0 , P ( A − B ) = P ( A ) − P ( B ) \because P(A-B)\geq 0,P(A-B)=P(A)-P(B) ∵P(A−B)≥0,P(A−B)=P(A)−P(B)
∴ P ( A ) ≥ P ( B ) \therefore P(A)\geq P(B) ∴P(A)≥P(B)
性质五(加法) ⋆ ⋆ ⋆ ⋆ ⋆ \star \star \star \star \star ⋆⋆⋆⋆⋆
P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B)−P(AB)
证:
A + B = A + ( B − A B ) A+B=A+(B-AB) A+B=A+(B−AB)
P ( A + B ) = P ( A ) + P ( B − A B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B-AB)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B−AB)=P(A)+P(B)−P(AB)
P ( B − A B ) = P ( B ) − P ( B ⋂ ( A B ) ) = P ( B ) − P ( A B ) P(B-AB)=P(B)-P(B\bigcap (AB))=P(B)-P(AB) P(B−AB)=P(B)−P(B⋂(AB))=P(B)−P(AB)
补: P ( A + B + C ) = P ( A ) + P ( B ) + P ( C ) − P ( A B ) − P ( A C ) − P ( B C ) + P ( A B C ) P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC) P(A+B+C)=P(A)+P(B)+P(C)−P(AB)−P(AC)−P(BC)+P(ABC)
例:A的概率0.4,B的概率0.3,A+B的概率0.6,求 P ( A B ˉ ) P(A \bar B) P(ABˉ)
P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B)−P(AB)
P ( A B ) = 0.1 P(AB)=0.1 P(AB)=0.1
P ( A B ˉ ) = P ( A − B ) = P ( A ) − P ( A B ) P(A\bar B)=P(A-B)=P(A)-P(AB) P(ABˉ)=P(A−B)=P(A)−P(AB)
P ( A B ˉ ) = 0.3 P(A \bar B )=0.3 P(ABˉ)=0.3
例: P ( A ) = P ( B ) = P ( C ) = 1 4 , P ( A B ) = 0 , P ( A C ) = P ( B C ) = 1 16 P(A)=P(B)=P(C)=\frac{1}{4},P(AB)=0,P(AC)=P(BC)=\frac{1}{16} P(A)=P(B)=P(C)=41,P(AB)=0,P(AC)=P(BC)=161,①A,B,C至少一个发生的概率②A,B,C都不发生概率
①
$P(A+B+C)=P(A)+P(B)+P©-P(AB)-P(AC)-P(BC)+P(ABC) $
= 3 4 − 0 − 2 16 + P ( A B C ) =\frac{3}{4}-0-\frac{2}{16}+P(ABC) =43−0−162+P(ABC)
$\because ABC\subset AB $
∴ 0 ≤ P ( A B C ) ≤ P ( A B ) = 0 \therefore 0 \leq P(ABC)\leq P(AB)=0 ∴0≤P(ABC)≤P(AB)=0
∴ P ( A B ) = 0 \therefore P(AB)=0 ∴P(AB)=0
P ( A + B + C ) = 5 8 P(A+B+C)=\frac{5}{8} P(A+B+C)=85
②
P ( A ˉ B ˉ C ˉ ) = 1 − P ( A + B + C ) = 3 8 P(\bar A \bar B \bar C)=1-P(A+B+C)=\frac{3}{8} P(AˉBˉCˉ)=1−P(A+B+C)=83
不 可 能 事 件 ϕ 的 概 率 P ( ϕ ) = 0 , 但 是 他 的 逆 命 题 不 成 立 不可能事件\phi 的概率P(\phi)=0,但是他的逆命题不成立 不可能事件ϕ的概率P(ϕ)=0,但是他的逆命题不成立
概 率 等 于 0 的 事 件 也 可 能 发 生 , 例 : 在 [ 0 , 1 ] 区 间 上 投 一 个 质 子 , 质 子 落 在 某 一 个 点 上 的 概 率 等 于 0 , 但 并 不 是 不 可 能 事 件 概率等于0的事件也可能发生,例:在[0,1]区间上投一个质子,质子落在某一个点上的概率等于0,但并不是不可能事件 概率等于0的事件也可能发生,例:在[0,1]区间上投一个质子,质子落在某一个点上的概率等于0,但并不是不可能事件
例:有4个白球 3个黑球,取3个球,至少两个白球的概率
C 4 2 C 3 1 + C 4 3 C 7 3 \frac{C_4^2C_3^1+C_4^3}{C_7^3} C73C42C31+C43
例:2台机器,第一台不需要看的概率为0.9,第二台不需要看的概率为0.8,两台都需要看的概率为0.02,至少一台需要看的概率
P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) = 0.1 + 0.2 − 0.02 = 0.28 P(A+B)=P(A)+P(B)-P(AB)=0.1+0.2-0.02=0.28 P(A+B)=P(A)+P(B)−P(AB)=0.1+0.2−0.02=0.28
例:20件产品一等品6件,二等品10件,三等品4件,取3件,至少2件等级相同的概率
至少2件等级相同的逆事件:3件等级都不相同
1 − C 6 1 C 10 1 C 4 1 C 20 3 = 15 19 1-\frac{C_6^1C_{10}^1C_4^1}{C_{20}^3}=\frac{15}{19} 1−C203C61C101C41=1915
例:(生日问题)n个人至少两人生日相同的概率
n个人至少两人生日相同的概率的逆事件:n个人生日各不相同
1 − 365 ! 36 5 n 1-\frac{365!}{365^n} 1−365n365!
n = 55 时 , 至 少 两 人 生 日 相 同 的 概 率 为 0.99 n=55时,至少两人生日相同的概率为0.99 n=55时,至少两人生日相同的概率为0.99
1.3.1条件概率
有男生50人,女生50人;其中,有30名男生和10名女生可以吃到月饼,在吃到月饼的学生中男生占 30 40 \frac{30}{40} 4030
定义: Ω 为 样 本 空 间 , A 、 B 两 个 事 件 P ( B ) > 0 , 在 B 已 经 发 生 的 条 件 下 A 发 生 的 概 率 就 是 A 对 B 的 条 件 概 率 , 记 作 P ( A ∣ B ) \Omega为样本空间,A、B两个事件P(B)>0,在B已经发生的条件下A发生的概率就是A对B的条件概率,记作P(A|B) Ω为样本空间,A、B两个事件P(B)>0,在B已经发生的条件下A发生的概率就是A对B的条件概率,记作P(A∣B)
P ( A ) 以 Ω 为 样 本 空 间 P(A)以\Omega为样本空间 P(A)以Ω为样本空间
P ( A ∣ B ) 以 B 为 样 本 空 间 P(A|B)以B为样本空间 P(A∣B)以B为样本空间
① P ( A ∣ B ) = n A B n B P(A|B)=\frac{n_{AB}}{n_B} P(A∣B)=nBnAB
② P ( A ∣ B ) = n A B / n n B / n = P ( A B ) P ( B ) P(A|B)=\frac{n_{AB}/n}{n_B/n}=\frac{P(AB)}{P(B)} P(A∣B)=nB/nnAB/n=P(B)P(AB)
例:1~6 6个球 B:取的号码为偶数 A 1 A_1 A1表示取的号码是1号 A 2 A_2 A2表示取的号码是2号 A 3 表 示 取 的 号 码 大 于 4 A_3表示取的号码大于4 A3表示取的号码大于4
P ( A 1 ) = 1 6 P(A_1)=\frac{1}{6} P(A1)=61
P ( A 1 ∣ B ) = 0 P(A_1|B)=0 P(A1∣B)=0
P ( A 2 ) = 1 6 P(A_2)=\frac{1}{6} P(A2)=61
P ( A 1 ∣ B ) = 1 3 P(A_1|B)=\frac{1}{3} P(A1∣B)=31
P ( A 3 ) = 2 6 P(A_3)=\frac{2}{6} P(A3)=62
P ( A 3 ∣ B ) = 1 3 P(A_3|B)=\frac{1}{3} P(A3∣B)=31
- P ( A ∣ B ) ≥ 0 P(A|B)\geq 0 P(A∣B)≥0
- P ( Ω ∣ B ) = 1 P(\Omega|B)=1 P(Ω∣B)=1
- A 1 , . . . , A n , . . . 不 相 容 , P ( ∑ i = 1 ∞ A i ∣ B ) = ∑ i = 1 ∞ P ( A i ∣ B ) A_1,...,A_n,...不相容,P(\sum_{i=1}^\infty A_i|B)=\sum_{i=1}^\infty P(A_i|B) A1,...,An,...不相容,P(∑i=1∞Ai∣B)=∑i=1∞P(Ai∣B)
1.3.2乘法公式
P ( A ∣ B ) = P ( A B ) P ( B ) , P ( B ∣ A ) = P ( A B ) P ( A ) , P ( A ) > 0 , P ( B ) > 0 P(A|B)=\frac{P(AB)}{P(B)},P(B|A)=\frac{P(AB)}{P(A)},P(A)>0,P(B)>0 P(A∣B)=P(B)P(AB),P(B∣A)=P(A)P(AB),P(A)>0,P(B)>0
① P ( A B ) = P ( B ) P ( A ∣ B ) P(AB)=P(B)P(A|B) P(AB)=P(B)P(A∣B)
② P ( A B ) = P ( A ) P ( B ∣ A ) P(AB)=P(A)P(B|A) P(AB)=P(A)P(B∣A)
P ( A 1 , A 2 , . . . , A n ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 A 2 ) … P ( A n ∣ A 1 . . . A n − 1 ) P(A_1,A_2,...,A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1A_2) \dots P(A_n|A_1...A_{n-1}) P(A1,A2,...,An)=P(A1)P(A2∣A1)P(A3∣A1A2)…P(An∣A1...An−1)
P ( A B C ) = P ( A ) P ( B ∣ A ) P ( C ∣ A B ) P(ABC)=P(A)P(B|A)P(C|AB) P(ABC)=P(A)P(B∣A)P(C∣AB)
例:共有产品100件,次品率10%,不放回取3次,第3次才取到合格品的概率
设 A 1 , A 2 , A 3 A_1,A_2,A_3 A1,A2,A3表示第1,2,3次取合格品
P ( A ˉ 1 A ˉ 2 A 3 ) = P ( A ˉ 1 ) P ( A ˉ 2 ∣ A ˉ 1 ) P ( A 3 ∣ A ˉ 1 A ˉ 2 ) = 10 100 × 9 99 × 90 98 = 0.00835 P(\bar A_1 \bar A_2A_3)=P(\bar A_1)P(\bar A_2|\bar A_1)P(A_3|\bar A_1 \bar A_2)=\frac{10}{100}\times \frac{9}{99} \times \frac{90}{98}=0.00835 P(Aˉ1Aˉ2A3)=P(Aˉ1)P(Aˉ2∣Aˉ1)P(A3∣Aˉ1Aˉ2)=10010×999×9890=0.00835
例:灯泡甲占60%,乙占40%,甲的合格率90%,乙的合格率80%
1.是甲厂且合格的概率 2.是乙场且合格的概率
假设灯泡是甲厂的事件为A,是乙厂的事件为 A ˉ \bar A Aˉ,灯泡是合格的事件为B,灯泡不合格的事件为 B ˉ \bar B Bˉ
1. P ( A B ) = P ( A ) P ( B ∣ A ) = 0.6 ∗ 0.9 = 0.54 P(AB)=P(A)P(B|A)=0.6*0.9=0.54 P(AB)=P(A)P(B∣A)=0.6∗0.9=0.54
2. P ( A ˉ B ) = P ( A ˉ ) P ( B ∣ A ˉ ) = 0.4 ∗ 0.8 = 0.32 P(\bar AB)=P(\bar A)P(B|\bar A)=0.4*0.8=0.32 P(AˉB)=P(Aˉ)P(B∣Aˉ)=0.4∗0.8=0.32
例:10张签其中4张难签,甲乙丙3人抽签,求1)甲抽中难签的概率2)甲和乙抽到难签的概率3)甲抽到易签乙抽到难签的概率4)三人都抽到难签的概率
A , B , C 分 别 表 示 甲 乙 丙 抽 到 难 签 A,B,C分别表示甲乙丙抽到难签 A,B,C分别表示甲乙丙抽到难签
1) P ( A ) = 4 10 P(A)=\frac{4}{10} P(A)=104
2) P ( A B ) = P ( A ) P ( B ∣ A ) = 4 10 × 3 9 = 4 30 P(AB)=P(A)P(B|A)=\frac{4}{10} \times \frac{3}{9}=\frac{4}{30} P(AB)=P(A)P(B∣A)=104×93=304
3) P ( A ˉ B ) = P ( A ˉ ) P ( B ∣ A ˉ ) = 6 10 × 4 9 = 4 15 P(\bar AB)=P(\bar A)P(B|\bar A)=\frac{6}{10}\times \frac{4}{9}=\frac{4}{15} P(AˉB)=P(Aˉ)P(B∣Aˉ)=106×94=154
4) P ( A B C ) = P ( A ) P ( B ∣ A ) P ( C ∣ A B ) = 4 10 × 3 9 × 2 8 = 1 30 P(ABC)=P(A)P(B|A)P(C|AB)=\frac{4}{10}\times \frac{3}{9}\times\frac{2}{8}=\frac{1}{30} P(ABC)=P(A)P(B∣A)P(C∣AB)=104×93×82=301
例:传染病模型——有a个红球,b个黑球,放入c个颜色相同的球,求连续三次都是红球的概率
设 A 1 A 2 A 3 A_1A_2A_3 A1A2A3表示第1,2,3次都摸到红球
P ( A 1 A 2 A 3 ) = a a + b a + c a + b + c a + 2 c a + b + 2 c P(A_1A_2A_3)=\frac{a}{a+b}\frac{a+c}{a+b+c}\frac{a+2c}{a+b+2c} P(A1A2A3)=a+baa+b+ca+ca+b+2ca+2c
c=0相当于摸完球就放回
c=-1相当于摸完球不放回
c>0每次放入c个颜色相同的球
1.4.1全概率公式
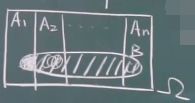
定理1.2: A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An是试验E的完备事件组, P ( A i ) > 0 P(A_i)>0 P(Ai)>0,B是任意的事件,则有
P ( B ) = ∑ i = 1 n P ( A i ) P ( B ∣ A i ) P(B)=\sum_{i=1}^nP(A_i)P(B|A_i) P(B)=∑i=1nP(Ai)P(B∣Ai)
例:四条生产线
| 一号生产线 | 二号生产线 | 三号生产线 | 四号生产线 | |
|---|---|---|---|---|
| 产量占比 | 15% | 20% | 30% | 35% |
| 不合格率 | 0.05 | 0.04 | 0.03 | 0.02 |
设 A 1 , A 2 , A 3 , A 4 A_1,A_2,A_3,A_4 A1,A2,A3,A4分别表示四条生产线生产的产品,B表示不合格
P ( B ) = P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) + P ( A 3 ) P ( B ∣ A 3 ) + P ( A 4 ) P ( B ∣ A 4 ) P(B)=P(A_1)P(B|A_1)+P(A_2)P(B|A_2)+P(A_3)P(B|A_3)+P(A_4)P(B|A_4) P(B)=P(A1)P(B∣A1)+P(A2)P(B∣A2)+P(A3)P(B∣A3)+P(A4)P(B∣A4)
0.15 ∗ 0.05 + 0.2 ∗ 0.04 + 0.3 ∗ 0.03 + 0.35 ∗ 0.02 0.15*0.05+0.2*0.04+0.3*0.03+0.35*0.02 0.15∗0.05+0.2∗0.04+0.3∗0.03+0.35∗0.02
例:
10台收音机 有3台次品,7台正品,已售两台,问再取一台是正品的概率
假设B表示第三次是正品, A 0 A_0 A0表示前两台都是次品, A 1 A_1 A1表示前两台一台是次品一台是正品, A 2 A_2 A2表示两台都是正品
P ( B ) = P ( A 0 ) P ( B ∣ A 0 ) + P ( A 1 ) P ( B ∣ A 1 ) + P ( A 2 ) P ( B ∣ A 2 ) P(B)=P(A_0)P(B|A_0)+P(A_1)P(B|A_1)+P(A_2)P(B|A_2) P(B)=P(A0)P(B∣A0)+P(A1)P(B∣A1)+P(A2)P(B∣A2)
= C 3 2 C 10 2 × 7 8 + C 3 1 C 7 1 C 10 2 × 6 8 + C 7 2 C 10 2 × 5 8 =\frac{C_3^2}{C_{10}^2}\times\frac{7}{8}+\frac{C_3^1C_7^1}{C_{10}^2}\times\frac{6}{8}+\frac{C_7^2}{C_{10}^2}\times\frac{5}{8} =C102C32×87+C102C31C71×86+C102C72×85
= 0.7 =0.7 =0.7
例:
10件产品,
| 次品的出现次数 | 概率 |
|---|---|
| 0次 | 1 3 \frac{1}{3} 31 |
| 1次 | 1 3 \frac{1}{3} 31 |
| 2次 | 1 3 \frac{1}{3} 31 |
检验有失误,正品被检测为次品的概率为0.02,次品被检验成正品的概率为0.05,问产品能通过验证的可能性
假设B是通过验证, A 0 , A 1 , A 2 A_0,A_1,A_2 A0,A1,A2表示出现0次,1次,2次次品, B 1 B_1 B1表示抽的是正品, B ˉ 1 \bar B_1 Bˉ1表示抽的是次品
P ( A 0 ) = 1 3 , P ( A 1 ) = 1 3 , P ( A 2 ) = 1 3 P(A_0)=\frac{1}{3},P(A_1)=\frac{1}{3},P(A_2)=\frac{1}{3} P(A0)=31,P(A1)=31,P(A2)=31
P ( B 1 ∣ A 0 ) = 1 , P ( B 1 ∣ A 1 ) = 9 10 . P ( B 1 ∣ A 2 ) = 8 10 P(B_1|A_0)=1,P(B_1|A_1)=\frac{9}{10}.P(B_1|A_2)=\frac{8}{10} P(B1∣A0)=1,P(B1∣A1)=109.P(B1∣A2)=108
P ( B 1 ) = P ( A 0 ) P ( B 1 ∣ A 0 ) + P ( A 1 ) P ( B 1 ∣ A 1 ) + P ( A 2 ) P ( B 1 ∣ A 2 ) = 0.9 , P ( B ˉ ) = 0.1 P(B_1)=P(A_0)P(B_1|A_0)+P(A_1)P(B_1|A_1)+P(A_2)P(B_1|A_2)=0.9,P(\bar B)=0.1 P(B1)=P(A0)P(B1∣A0)+P(A1)P(B1∣A1)+P(A2)P(B1∣A2)=0.9,P(Bˉ)=0.1
P ( B ) = P ( B 1 ) P ( B ∣ B 1 ) + P ( B ˉ 1 ) P ( B ∣ B ˉ 1 ) = 0.9 ∗ ( 1 − 0.02 ) + 0.1 ∗ 0.05 = 0.887 P(B)=P(B_1)P(B|B1)+P(\bar B_1)P(B|\bar B_1)=0.9*(1-0.02)+0.1*0.05=0.887 P(B)=P(B1)P(B∣B1)+P(Bˉ1)P(B∣Bˉ1)=0.9∗(1−0.02)+0.1∗0.05=0.887
1.4.2贝叶斯公式
A 1 . . . A n A_1...A_n A1...An完备 P ( A i ) ≥ 0 , P ( B ) ≥ 0 P(A_i)\geq 0,P(B)\geq 0 P(Ai)≥0,P(B)≥0
P ( A k ∣ B ) = P ( A k ) P ( B ∣ A k ) ∑ i = 1 n P ( A i ) P ( B ∣ A i ) = P ( A k B ) P ( B ) P(A_k|B)=\frac{P(A_k)P(B|A_k)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)}=\frac{P(A_kB)}{P(B)} P(Ak∣B)=∑i=1nP(Ai)P(B∣Ai)P(Ak)P(B∣Ak)=P(B)P(AkB)
P ( A i ) P(A_i) P(Ai)先验概率
P ( A i ∣ B ) P(A_i|B) P(Ai∣B)后验概率
例:发病率0.0004,一个患者经过检验确诊有病99%,诊断为没病1%,一个健康的人经过检验有病0.1%,没病99.9%。现有一人经过检验发现有病,则此人真有病的概率为多少
A:患病 A ˉ \bar A Aˉ:健康 B:检验有病
P ( A ) = 0.0004 P(A)=0.0004 P(A)=0.0004
P ( A ˉ ) = 0.9996 P(\bar A)=0.9996 P(Aˉ)=0.9996
P ( B ∣ A ) = 0.99 P(B|A)=0.99 P(B∣A)=0.99
P ( B ∣ A ˉ ) = 0.001 P(B|\bar A)=0.001 P(B∣Aˉ)=0.001
P ( B ) = P ( A ) P ( B ∣ A ) + P ( A ˉ ) P ( B ∣ A ˉ ) = 0.0013956 P(B)=P(A)P(B|A)+P(\bar A)P(B|\bar A)=0.0013956 P(B)=P(A)P(B∣A)+P(Aˉ)P(B∣Aˉ)=0.0013956
P ( A ∣ B ) = P ( A B ) P ( B ) = P ( A ) P ( B ∣ A ) P ( B ) = 0.0004 × 0.99 0.0013956 = 0.284 P(A|B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B|A)}{P(B)}=\frac{0.0004\times0.99}{0.0013956}=0.284 P(A∣B)=P(B)P(AB)=P(B)P(A)P(B∣A)=0.00139560.0004×0.99=0.284
1.5.1事件的独立性
定义:A事件的概率不受B发生与否的影响
P ( A ∣ B ) = P ( A ) P(A|B)=P(A) P(A∣B)=P(A)
定理:若 P ( A ) > 0 , P ( B ) > 0 P(A)>0,P(B)>0 P(A)>0,P(B)>0
A 、 B 独 立 ⇔ P ( A B ) = P ( A ) P ( B ) A、B独立\Leftrightarrow P(AB)=P(A)P(B) A、B独立⇔P(AB)=P(A)P(B)
证: 充分 P ( A B ) = P ( A ) P ( B ) , P ( A ∣ B ) = P ( A B ) P ( B ) = P ( A ) P ( B ) P ( B ) = P ( A ) P(AB)=P(A)P(B),P(A|B)=\frac{P(AB)}{P(B)}=\frac{P(A)P(B)}{P(B)}=P(A) P(AB)=P(A)P(B),P(A∣B)=P(B)P(AB)=P(B)P(A)P(B)=P(A)
必要 A 、 B 独 立 , P ( A ∣ B ) = P ( A ) A、B独立,P(A|B)=P(A) A、B独立,P(A∣B)=P(A)
P ( A B ) = P ( B ) P ( A ∣ B ) = P ( B ) P ( A ) P(AB)=P(B)P(A|B)=P(B)P(A) P(AB)=P(B)P(A∣B)=P(B)P(A)
补:当 P ( A ) = 0 或 P ( B ) = 0 P(A)=0或P(B)=0 P(A)=0或P(B)=0时, P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)也成立
设 P ( A ) = 0 , A B ⊂ A , 0 ≤ P ( A B ) ≤ P ( A ) = 0 P(A)=0, AB\subset A,0\leq P(AB) \leq P(A) = 0 P(A)=0,AB⊂A,0≤P(AB)≤P(A)=0
P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
定义: 若 P ( A B ) = P ( A ) P ( B ) , 则 A 、 B 两 个 事 件 独 立 若P(AB)=P(A)P(B),则A、B两个事件独立 若P(AB)=P(A)P(B),则A、B两个事件独立
ϕ 、 Ω 与 任 意 事 件 A 独 立 \phi、\Omega 与任意事件A独立 ϕ、Ω与任意事件A独立
定理:(1)如果A、B独立,则 A 与 B ˉ A与\bar B A与Bˉ A ˉ 与 B \bar A 与 B Aˉ与B $ \bar A 与 \bar B$独立
(2)P(A)=0或P(A)=1,A与任意事件独立
证:
(1) P ( A B ˉ ) = P ( A − B ) = P ( A − A B ) = P ( A ) − P ( A ) P ( B ) = P ( A ) ( 1 − P ( B ) ) = P ( A ) P ( B ˉ ) P(A \bar B)=P(A-B)=P(A-AB)=P(A)-P(A)P(B)=P(A)(1-P(B))=P(A)P(\bar B) P(ABˉ)=P(A−B)=P(A−AB)=P(A)−P(A)P(B)=P(A)(1−P(B))=P(A)P(Bˉ)
(2) P ( A ) = 0 , A B ⊂ A , 0 ≤ P ( A B ) ≤ P ( A ) = 0 P(A)=0,AB\subset A,0\leq P(AB)\leq P(A)= 0 P(A)=0,AB⊂A,0≤P(AB)≤P(A)=0
P ( A ) = 1 , P ( A ˉ ) = 0 , A ˉ 与 B 独 立 , 则 A 与 B 独 立 P(A)=1,P(\bar A)=0,\bar A与B独立,则A与B独立 P(A)=1,P(Aˉ)=0,Aˉ与B独立,则A与B独立
独立:可能性
互不相容: A B = ϕ AB=\phi AB=ϕ
P(A)>0,P(B)>0时,独立与互不相容不同时成立
三个事件独立
-
P(AB)=P(A)P(B)
-
P(BC)=P(B)P©
-
P(AC)=P(A)P©
-
P(ABC)=P(A)P(B)P©
例: P ( A + B ) = 0.9 , P ( A ) = 0.4 , 求 P ( B ) P(A+B)=0.9,P(A)=0.4,求P(B) P(A+B)=0.9,P(A)=0.4,求P(B)
-
A、B互不相容: A B = ϕ , P ( A B ) = 0 AB=\phi,P(AB)=0 AB=ϕ,P(AB)=0
P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) P(A+B)=P(A)+P(B)-P(AB) P(A+B)=P(A)+P(B)−P(AB)
P ( B ) = P ( A + B ) − P ( A ) = 0.5 P(B)=P(A+B)-P(A)=0.5 P(B)=P(A+B)−P(A)=0.5
-
A、B独立: P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
P ( A + B ) = P ( A ) + P ( B ) − P ( A B ) = P ( A ) + P ( B ) − P ( A ) P ( B ) P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B) P(A+B)=P(A)+P(B)−P(AB)=P(A)+P(B)−P(A)P(B)
P ( B ) = 5 6 P(B)=\frac{5}{6} P(B)=65
例:甲乙丙各投篮一次,投中概率分别为0.7,0.8,0.75
设甲投中为A、乙投中为B、丙投中为C
1)恰有一人投中的概率
P ( A B ˉ C ˉ + A ˉ B C ˉ + A ˉ B ˉ C ) P(A\bar B \bar C+\bar A B \bar C +\bar A \bar B C) P(ABˉCˉ+AˉBCˉ+AˉBˉC)
= P ( A B ˉ C ˉ ) + P ( A ˉ B C ˉ ) + P ( A ˉ B ˉ C ) =P(A\bar B \bar C)+P(\bar A B \bar C )+P(\bar A \bar B C) =P(ABˉCˉ)+P(AˉBCˉ)+P(AˉBˉC)
= P ( A ) P ( B ˉ ) P ( C ˉ ) + P ( A ˉ ) P ( B ) P ( C ˉ ) + P ( A ˉ ) P ( B ˉ ) P ( C ) =P(A)P(\bar B)P(\bar C)+P(\bar A)P(B)P(\bar C)+P(\bar A)P(\bar B)P(C) =P(A)P(Bˉ)P(Cˉ)+P(Aˉ)P(B)P(Cˉ)+P(Aˉ)P(Bˉ)P(C)
2)三人都投中
P ( A B C ) = P ( A ) P ( B ) P ( C ) P(ABC)=P(A)P(B)P(C) P(ABC)=P(A)P(B)P(C)
3)至少一人投中
逆命题 → \rightarrow →三人都没投中
P ( A + B + C ) = 1 − P ( A ˉ B ˉ C ˉ ) = 1 − P ( A ˉ ) P ( B ˉ ) P ( C ˉ ) P(A+B+C)=1-P(\bar A \bar B \bar C)=1-P(\bar A)P(\bar B)P(\bar C) P(A+B+C)=1−P(AˉBˉCˉ)=1−P(Aˉ)P(Bˉ)P(Cˉ)
例:破译密码,每个人破译密码的概率是0.6,若要以99%的概率破译出密码,则至少需要几人?
解:
A i 第 i 个 人 破 译 出 来 , B = ⋃ i = 1 n A ˉ i A_i第i个人破译出来,B=\bigcup _{i=1}^n \bar A_i Ai第i个人破译出来,B=⋃i=1nAˉi
P ( B ) = 1 − P ( ⋂ i = 1 n A ˉ i ) = 1 − ∏ i = 1 n P ( A ˉ i ) = 1 − 0. 4 n P(B)=1-P(\bigcap _{i=1}^n \bar A_i)=1-\prod_{i=1}^n P(\bar A_i)=1-0.4^n P(B)=1−P(⋂i=1nAˉi)=1−∏i=1nP(Aˉi)=1−0.4n
1 − 0. 4 n ≥ 0.99 1-0.4^n\geq0.99 1−0.4n≥0.99
n ≈ 5.026 n\approx 5.026 n≈5.026
$\therefore n=6 $
例: 0 < P ( A ) < 1 , 0 < P ( B ) < 1 , P ( A ∣ B ) + P ( A ˉ ∣ B ˉ ) = 1 0
P ( A ∣ B ˉ ) + P ( A ˉ ∣ B ˉ ) = 1 P(A|\bar B)+P(\bar A|\bar B)=1 P(A∣Bˉ)+P(Aˉ∣Bˉ)=1
在 B ˉ 发 生 的 情 况 下 , A 发 生 的 概 率 + A ˉ 发 生 的 概 率 = 1 在\bar B发生的情况下,A发生的概率+\bar A发生的概率=1 在Bˉ发生的情况下,A发生的概率+Aˉ发生的概率=1
∴ P ( A ∣ B ) = P ( A ∣ B ˉ ) \therefore P(A|B)=P(A|\bar B) ∴P(A∣B)=P(A∣Bˉ)
P ( A B ) P ( B ) = P ( A B ˉ ) P ( B ˉ ) = P ( A − A B ) 1 − P ( B ) = P ( A ) − P ( A B ) 1 − P ( B ) \frac{P(AB)}{P(B)}=\frac{P(A\bar B)}{P(\bar B)}=\frac{P(A-AB)}{1-P(B)}=\frac{P(A)-P(AB)}{1-P(B)} P(B)P(AB)=P(Bˉ)P(ABˉ)=1−P(B)P(A−AB)=1−P(B)P(A)−P(AB)
P ( A B ) − P ( B ) P ( A B ) = P ( A ) P ( B ) − P ( B ) P ( A B ) P(AB)-P(B)P(AB)=P(A)P(B)-P(B)P(AB) P(AB)−P(B)P(AB)=P(A)P(B)−P(B)P(AB)
P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
∴ A 、 B 独 立 \therefore A、B独立 ∴A、B独立
1.5.2伯努利模型
独立实验序列: E 1 , E 2 , . . . , E n E_1,E_2,...,E_n E1,E2,...,En独立,(做n次不同的实验)
n重独立实验: E , E , . . . , E E,E,...,E E,E,...,E独立, E n E^n En(一个实验重复做n次)
伯努利实验:结果只有两种
n重伯努利:实验做n次,每次实验之间独立,结果只有两种
定理:A的概率 P ( 0 < P < 1 ) P(0
n重伯努利中A发生k次的概率:
P n ( k ) = C n k P k ( 1 − P ) n − k = C n k P k q n − k , q = 1 − p P_n(k)=C_n^kP^k(1-P)^{n-k}=C_n^kP^kq^{n-k},q=1-p Pn(k)=CnkPk(1−P)n−k=CnkPkqn−k,q=1−p二次概率公式
例1:
一批产品,废品率0.1,合格率0.9,每次取一个又放回,取三次
(1)恰有一次取废品
C 3 1 × 0.1 × 0. 9 2 C_3^1\times 0.1 \times 0.9^2 C31×0.1×0.92
(2)恰有两次取废品
C 3 2 × 0. 1 2 × 0.9 C_3^2\times 0.1^2\times0.9 C32×0.12×0.9
(3)三次都取废品
C 3 3 × 0. 1 3 C_3^3\times 0.1^3 C33×0.13
(4)三次都取正品
C 3 0 × 0. 9 3 C_3^0\times0.9^3 C30×0.93
例2:
彩票每周开奖一次中奖率是十万分之一
十年买了520次,从未中奖的概率
P 520 ( 0 ) = C 520 0 ( 1 − 1 0 − 5 ) 520 ( 1 0 − 5 ) 0 ≈ 0.9948 P_{520}(0)=C_{520}^0(1-10^{-5})^{520}(10^{-5})^0\thickapprox0.9948 P520(0)=C5200(1−10−5)520(10−5)0≈0.9948