《机器学习实战》7.AdaBoost元算法提高分类性能

目录

1 基于数据集多重抽样的分类器

1.1 bagging：基于数据随机重抽样的分类器构建方法

1.2 boosting

2 训练算法：基于错误提升分类器的性能

3 基于单层决策树后见弱分类器

4 完整AdaBoost算法的实现

5 测试算法：基于AdaBoost的分类

6 示例：在一个数据集上应用AdaBoost

7 非均衡分类问题

 7.1 其他分类性能度量指标：正确率、召回率及ROC曲线

7.2 基于代价函数的分类器决策控制

7.3 处理非均衡问题的数据抽样方法

---

本章涉及到的相关代码和数据

本章内容：

①组合相似的分类器来提高分类性能

②应用AdaBoost算法

③处理分均衡分类问题

元算法背后的思路：考虑吸取多个专家而不只是一个人的意见

1 基于数据集多重抽样的分类器

我已经学到了五种不同的分类算法，它们各有优缺点。我们可以将不同的分类器组合起来，而这种组合结果则被称为集成方法或者元算法。使用集成方法时会有多种形式：可以是不同算法的集成呢个、也可以是同意算法在不同设置下的集成，还可以时数据集不同部分分配给不同分类器之后的集成。  

AdaBoost：  

优点：泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整  

缺点：对离群点敏感  

适用数据类型：数值型和标称型数据  

1.1 bagging：基于数据随机重抽样的分类器构建方法

自举汇聚法（bootstrap aggregating），也称bagging方法，是在从原始数据集选择s次后得到s个新数据集的一种技术。新数据集和原数据集大小相等。每个数据集都是通过在原始数据集中随机选择一个样本来进行替换而得到的。这里的替换就意味着可以多次地选择同一个样本。这一性质就允许新数据集中可以有重复的值，而原始数据集的某些值在新集合中则不再出现。  

在s个数据集建好之后，将某个学习算法分别作用于每个数据集就得到了s个分类器。当我们要对新数据进行分类时，就可以应用这s个分类器进行分类。与此同时，选择分类器投票结果中最多的类别作为最后的分类结果。  

1.2 boosting

boosting是一种与bagging很类似的技术。不论是在boosting还是bagging当中，所使用的多个分类器的类型都是一致的。答案是在前者当中，不同的分类器时通过串行训练而获得的，每个新分类器都根据已训练出的分类器的性能来进行训练。boosting时通过几种关注被已有分类器错分的那些数据来获得新的分类器。  

由于boosting分类的结果时基于所有分类器的加权求和结果的，因此boosting与bagging不太一样，bagging中的分类器权重是相等的，而boosting中的分类器权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。  

AdaBoost的一般流程：  

①收集数据：可以使用任意方法  

②准备数据：依赖于所使用的弱分类器类型，本章使用的是单层决策树，这种分类器可以处理任意数据类型。当然也可以使用任意分类器作为弱分类器（k临近算法、决策树算法、朴素贝叶斯、logistic回归、支持向量机都可），作为弱分类器，简单分类器的效果更好  

③分析数据：可以使用任意方法    

④训练算法：A大Boost的大部分时间都用在训练上，分类器将多次在同一数据集上训练弱分类器    

⑤测试算法：计算分类的错误率  

⑥使用算法：同SVM一样，ADaBoost预测两个类别中的一个。弱国想将她应用到多个类别的场合，那么就要像多类SVM中的做法一样对AdaBoost进行修改。

2 训练算法：基于错误提升分类器的性能

AdaBoost是adaptive boosting的缩写，其运行过程如下：训练数据中的每个样本，并赋予其一个权重，这些权重构成了向量D。一开始，这些权重都初始化成相等值。首先在训练数据上村联储一个弱分类器并计算该分类器的错误率，然后在同一数据集上再次训练弱分类器，在分类器的第二次训练当中，将会重新调整每个样本的权重，其中第一次分对的样本的权重将会降低，饿第一次分错的样本的权重将会提高。为了从所有弱分类器中得到最终的分类结果，AdaBoost为每个分类器都分配了一个权重值alpha，这些alpha值是基于每个弱分类器的错误率进行计算的。

3 基于单层决策树后见弱分类器

单层决策树是一种简单的决策树。这棵树只有一次分裂过程，因此实际上他就是一个树桩。

import numpy as np
def loadSimpleData():
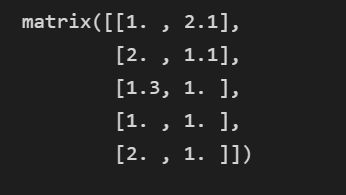
    datMat=np.matrix([[1.,2.1],[2.,1.1],[1.3,1.],[1.,1.],[2.,1.]])
    classLabels=[1.0,1.0,-1.0,-1.0,1.0]
    return datMat,classLabels

datMat,classLabels=loadSimpleData()
datMat

运行结果为：

有了数据之后，接下来就可以通过构建多个函数来建立单层决策树。  

第一个函数将用于测试是否有某个值小于或者大于我们正在测试的阙值。第二个函数则更加复杂一些，他会在一个加权数据集中循环，并找到最低错误率的单层决策树。  

伪代码大致如下：  

将最小错误率minError设置为正无穷  

对数据集中的每一个特征（第一层循环）：  

    对每个步长（第二层循环）：  

        对每个不等号（第三层循环）：  

            建立一颗单层决策树并利用加权数据集对他进行测试  

            如果错误率低于minError，则将当前决策树设为最佳单层决策树  

返回最佳单层决策树  

 

from cmath import inf

                #  数组 阙值  
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):
    retArray=np.ones((np.shape(dataMatrix)[0],1))
    if threshIneq=='lt':
        retArray[dataMatrix[:,dimen]<=threshVal]=-1.0
    else:
        retArray[dataMatrix[:,dimen]>threshVal]=-1.0
    return retArray


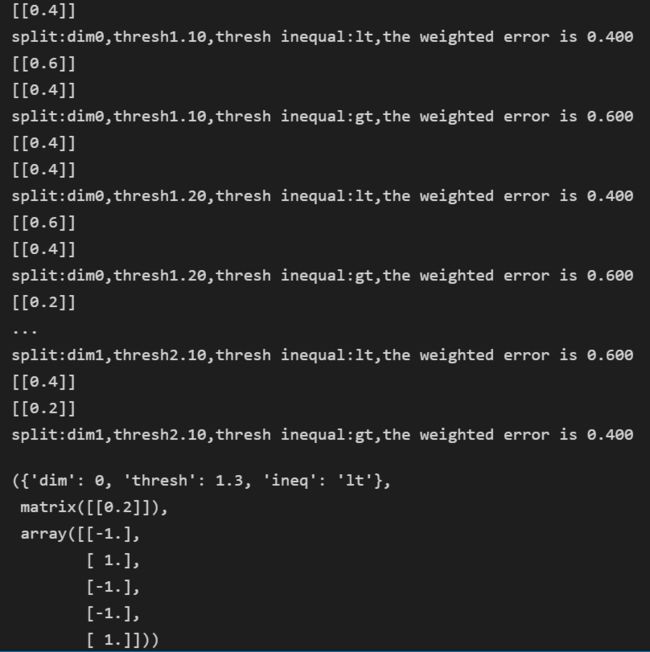
def buildStump(dataArr,classLabels,D):
    dataMatrix=np.mat(dataArr)
    labelMat=np.mat(classLabels).T
    m,n=np.shape(dataMatrix)
    numSteps=10.0
    bestStump={}
    bestClasEst=np.mat(np.zeros((m,1)))
    # inf表示无穷大
    minError=inf
    # 第一个循环：对数据集中的每个特征
    for i in range(n):
        rangeMin=dataMatrix[:,i].min()
        rangeMax=dataMatrix[:,i].max()
        stepSize=(rangeMax-rangeMin)/numSteps
        # 第二层循环：对每个步长
        for j in range(-1,int(numSteps)+1):
            # 第三层循环：对每个不等号
            for inequal in ['lt','gt']:
                threshVal=(rangeMin+float(j)*stepSize)
                predictedVals=stumpClassify(dataMatrix,i,threshVal,inequal)
                errArr=np.mat(np.ones((m,1)))
                errArr[predictedVals==labelMat]=0
                weightedError=D.T*errArr
                print(weightedError)
                print(minError)
                print("split:dim%d,thresh%0.2f,thresh inequal:%s,the weighted error is %0.3f" % (i,threshVal,inequal,weightedError))
                if weightedError

代码运行结果为：

4 完整AdaBoost算法的实现

伪代码：

对每次迭代：

    利用buildStump（）函数找到最佳的单层决策树

    将最佳的单层决策树加入到单层决策树数组

    计算alpha

    计算新的权重向量D

    更新累计类别估计值

    如果错误率等于0.0，则退出循环

from math import *
# import math
from numpy import *
import decimal

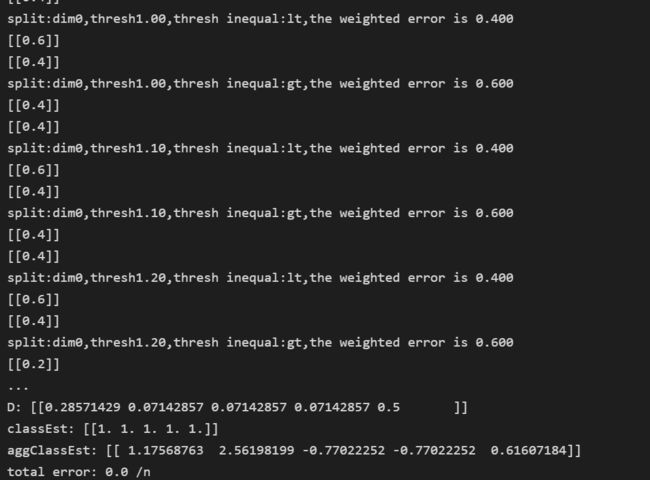
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
    weakClassArr=[]
    m=np.shape(dataArr)[0]
    D=np.mat(np.ones((m,1))/m)
    aggClassEst=np.mat(np.zeros((m,1)))
    # 进入循环
    for i in range(numIt):
        bestStump,error,classEst=buildStump(dataArr,classLabels,D)
        print("D:",D.T)
        alpha=float(0.5*log((1.0-error)/max(error,1e-16)))
        bestStump['alpha']=alpha
        weakClassArr.append(bestStump)
        print("classEst:",classEst.T)
        expon=np.multiply(-1*alpha*np.mat(classLabels).T,classEst)
        D=np.multiply(D,exp(expon))
        D=D/D.sum()
        aggClassEst += alpha*classEst
        print("aggClassEst:",aggClassEst.T)
        aggErrors=np.multiply(np.sign(aggClassEst)!=np.mat(classLabels).T,np.ones((m,1)))
        errorRate=aggErrors.sum()/m
        print("total error:",errorRate,"/n")
        # 直到训练错误率为0或者弱分类器的数目达到指定值
        if errorRate==0.0:
            break
    return weakClassArr
    # return weakClassArr,aggClassEst

classifierArr=adaBoostTrainDS(datMat,classLabels,9)

 代码运行结果为：

5 测试算法：基于AdaBoost的分类

 

# AdaBoost分类函数
# 利用训练出的多个弱分类器进行分类
    #           待分类样例  弱分类器组成的数组
def adaClassify(datToClass,classifierArr):
    # 先转换为矩阵、
    dataMatrix=np.mat(datToClass)
    # 得到待分类样例的个数
    m=shape(dataMatrix)[0]
    # 构建一个0列向量
    aggClassEst=np.mat(np.zeros((m,1)))
    # 遍历所有弱分类器
    for i in range(len(classifierArr)):
        # 得到每个分类器得到一个分类的估计值
        classEst=stumpClassify(dataMatrix,classifierArr[i]['dim'],classifierArr[i]['thresh'],classifierArr[i]['ineq'])
        # 得到分类结果
        aggClassEst+=classifierArr[i]['alpha']*classEst
        print (aggClassEst)
        # sign（）函数取数字前的符号（正负号）输出结果为1，0，-1
    return sign(aggClassEst)

adaClassify([0,0],classifierArr)

代码运行结果：

6 示例：在一个数据集上应用AdaBoost

示例：在一个难数据集上的AdaBoost应用

①收集数据：提供的文本文件

②准备数据：确保类别标签是1和-1，而不是1和0

③分析数据：手工检查数据

④训练算法：在数据上，利用AdaBoostTrainDS（）函数训练处一系列的分类器

⑤测试算法：我们拥有两个数据集。在不采用随机抽样的方法下，我们就会对AdaBoost和logistic回归的结果进行完全对等的比较

⑥使用算法：观察钙离子上的错误率。不过，也可以构建一个WEb网站，让驯马师输入马的症状然后预测马是否会立即死去。

 

# 自适应数据加载函数
def loadDataSet(fileName):
    numFeat=len(open(fileName).readline().split('\t'))
    dataMat=[]
    labelMat=[]
    fr=open(fileName)
    for line in fr.readlines():
        lineArr=[]
        curLine=line.strip().split('\t')
        for i in range(numFeat-1):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

datArr,labelArr=loadDataSet('horseColicTraining2.txt')
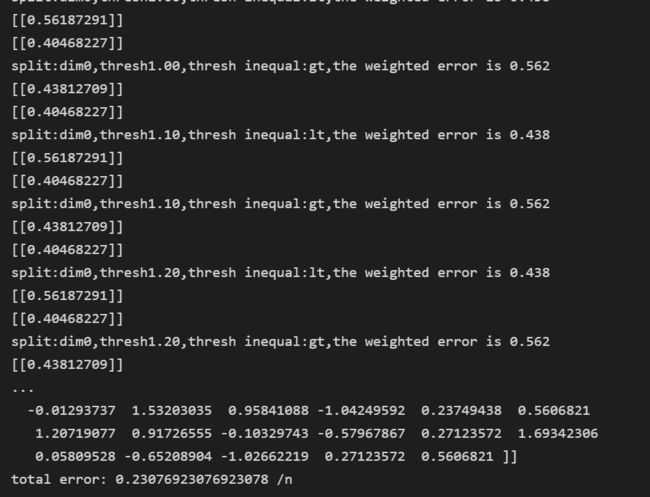
classifierArray=adaBoostTrainDS(datArr,labelArr,10)

代码运行结果：

testArr,testLabelArr=loadDataSet('horseColicTest2.txt')
prediction10=adaClassify(testArr,classifierArray)
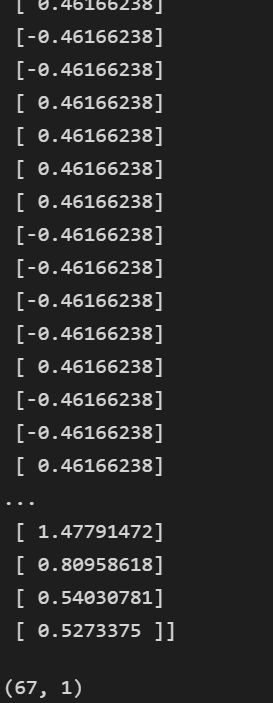
shape(prediction10)

代码运行结果：

 查看分错的样例个数：

errArr=np.mat(np.ones((67,1)))
# 分错的样例个数
errArr[prediction10!=np.mat(testLabelArr).T].sum()

代码运行结果：

7 非均衡分类问题

在之前的所有分类介绍中，我们都假设所有类别的分类代价是一样的。在这里，我们将会考察一种新的分类器性能度量方法，并通过图像技术来对上述非均衡问题下不同分类器的性能进行可视化处理。

 7.1 其他分类性能度量指标：正确率、召回率及ROC曲线

正确率：预测为正例的样本中的真正正例的比例

召回率：预测为正例的真实比例占所有真实正例的比例

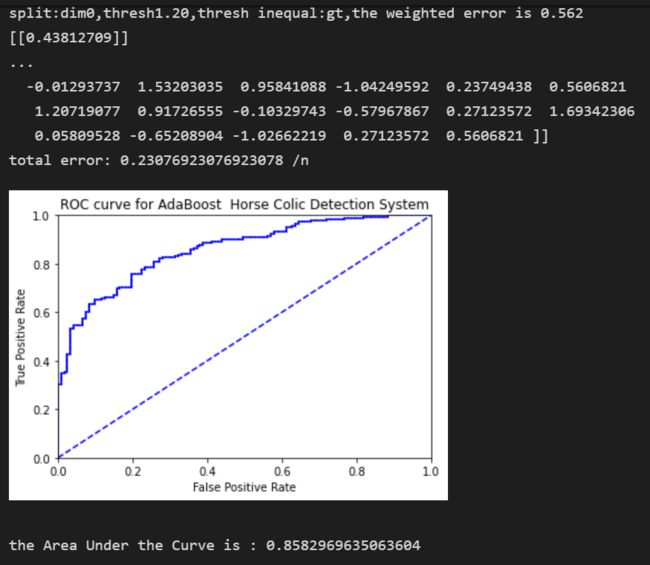
ROC曲线：ROC代表接收者操作特征；横轴是伪正例的比例（假阳率），纵轴是真正例的比例（真阳率）。ROC曲线给出饿是当阙值变化时假阳率和帧阳率的变化情况。虚线给出的是随机猜测的结果曲线。ROC曲线不但可以用于比较分类器，还可以基于成本效益分析来做出决策。在理想的情况下，最佳的分类器应该尽量地处于左上角，这就意味着在假阳率很低地情况下同时获得了很高地正阳率。对于不同ROC曲线进行比较地一个指标是曲线下地面积AUC，AUC给出地是分类器地平均性能值，一个完美分类器的AUC 为1.0。

 

# ROC曲线的绘制及AUction计算函数
#          分类器的预测强度 类别标签
def plotROC(predStrengths,classLabels):
    import matplotlib.pyplot as plt
    # 保存绘制光标的位置
    cur=(1.0,1.0)
    # 用于计算AUC的值
    ySum=0.0
    numPosClas=sum(array(classLabels)==1.0)
    # 得到步长
    yStep=1/float(numPosClas)
    xStep=1/float(len(classLabels)-numPosClas)
    sortedIndicies=predStrengths.argsort()
    fig=plt.figure()
    fig.clf()
    ax=plt.subplot(111)
    for index in sortedIndicies.tolist()[0]:
        if classLabels[index]==1.0:
            delX=0
            delY=yStep
        else:
            delX=xStep
            delY=0
            # 对小矩形面积进行累加
            ySum+=cur[1]
        # 绘制实线
        ax.plot([cur[0],cur[0]-delX],[cur[1],cur[1]-delY],c='b')
        cur=(cur[0]-delX,cur[1]-delY)
    # 绘制虚线
    ax.plot([0,1],[0,1],'b--')
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.title('ROC curve for AdaBoost  Horse Colic Detection System')
    ax.axis([0,1,0,1])
    plt.show()
    print("the Area Under the Curve is :",ySum*xStep)


def adaBoostTrainDS(dataArr,classLabels,numIt=40):
    weakClassArr=[]
    m=np.shape(dataArr)[0]
    D=np.mat(np.ones((m,1))/m)
    aggClassEst=np.mat(np.zeros((m,1)))
    # 进入循环
    for i in range(numIt):
        bestStump,error,classEst=buildStump(dataArr,classLabels,D)
        print("D:",D.T)
        alpha=float(0.5*log((1.0-error)/max(error,1e-16)))
        bestStump['alpha']=alpha
        weakClassArr.append(bestStump)
        print("classEst:",classEst.T)
        expon=np.multiply(-1*alpha*np.mat(classLabels).T,classEst)
        D=np.multiply(D,exp(expon))
        D=D/D.sum()
        aggClassEst += alpha*classEst
        print("aggClassEst:",aggClassEst.T)
        aggErrors=np.multiply(np.sign(aggClassEst)!=np.mat(classLabels).T,np.ones((m,1)))
        errorRate=aggErrors.sum()/m
        print("total error:",errorRate,"/n")
        # 直到训练错误率为0或者弱分类器的数目达到指定值
        if errorRate==0.0:
            break
    # return weakClassArr
    return weakClassArr,aggClassEst

datArr,albelArr=loadDataSet('horseColicTraining2.txt')
classifierArray,aggClassEst=adaBoostTrainDS(datArr,labelArr,10)
plotROC(aggClassEst.T,labelArr)

代码运行结果：

7.2 基于代价函数的分类器决策控制

除了调节分类器的阙值之外，我们还有一些其他可以用于处理非均匀代价问题的方法，其中一种称为代价敏感的学习。

7.3 处理非均衡问题的数据抽样方法

对分类器的训练数据进行改造，这可以通过欠抽样和过抽样来实现。过抽样意味着可以复制样例，而欠抽样则意味着可能会删除样例。