视觉SLAM十四讲学习第二部分(ch7-ch14)
Debug过程中遇到的问题
0、写在前言
题头诗:
初尝视觉SLAM,代码头挠秃
代码好在哪,看完云雾里
度娘google来回切,方知知易行难
这篇Debug的记录是按照章节组织的,内容包括但不限于如下的内容:
- 环境配置
- 代码解析
- 运行报错
- 其他杂项
每一个内容讲述的要点我都在小标题里有比较详细的说明,可以先查看目录看看是否有你遇到的疑问。
四、ch7
1. 代码解析:为什么手写ORB中,FAST特征点要保留方向,其又是怎么控制的Brief描述子的旋转一致性
这个问题的出发点,是在阅读教材时就存在的,FAST通过质点确定的方向的意义何在?这个方向角又是怎么帮助到BRIEF确定自身的旋转一致性的?
可以阅读手写ORB代码的这一段,其解释了FAST方向角theta如何确定BRIEF自身的旋转一致性:
cv::Point2f pp = cv::Point2f(cos_theta * p.x - sin_theta * p.y, sin_theta * p.x + cos_theta * p.y)+ kp.pt;
cv::Point2f qq = cv::Point2f(cos_theta * q.x - sin_theta * q.y, sin_theta * q.x + cos_theta * q.y) + kp.pt;
首先,Point2f内部是向量旋转公式,其作用是确定某一向量按 θ \theta θ角旋转后的新坐标。外部加的kp.pt是当前FAST特征点的绝对像素位置
首先解释一下向量旋转公式:
对于原像素坐标点 ( p x , p y ) (p_x,p_y) (px,py),将其旋转 θ \theta θ后,新的坐标点计算公式为:
首先, θ \theta θ对应的旋转矩阵为 R = [ c o s θ − s i n θ s i n θ c o s θ ] R=\begin{bmatrix}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} R=[cosθsinθ−sinθcosθ]
由此,新坐标点计算公式为 ( p p x , p p y ) = R ( p x , p y ) T (pp_x,pp_y)=R(p_x,p_y)^T (ppx,ppy)=R(px,py)T
而由于 ( p p x , p p y ) (pp_x,pp_y) (ppx,ppy)只是在以 ( p x , p y ) (p_x,p_y) (px,py)为原点的过度坐标系中,旋转 θ \theta θ后的坐标,要转化到像素坐标还有一个平移量,即 t = k p . p t t=kp.pt t=kp.pt,加上平移量后与代码中的计算是完全一致的
然后是上述步骤如何保证了BRIEF的旋转一致性:
之所以需要给描述子照FAST特征点的方向做旋转,是为了给Brief描述子赋予旋转不变性。
比如说,当前图片在微小旋转后得到了一个新的图,这个图仍然找到了之前的FAST特征点,如果FAST特征点没有方向,那么这一次基于ORB_pattern做的描述子就和之前的是不一样的。
而如果FAST特征点保留了方向性,且在计算Brief描述子的时候通过该角度对ORB_pattern给出的初始像素位置做了旋转,那么就可以保证两次计算的Brief描述子的一致性,即Brief描述子也具备了旋转一致性
那么这个方向性是如何定义的,且看书里面的原文:“灰度质心法”,旋转后所得的两幅图中对同一个角点求质心,质心与角点连线的向量始终是同一个,将所取描述子空间以向量角度旋转后,前后两幅图中的描述子空间是一致的,如下图所示:
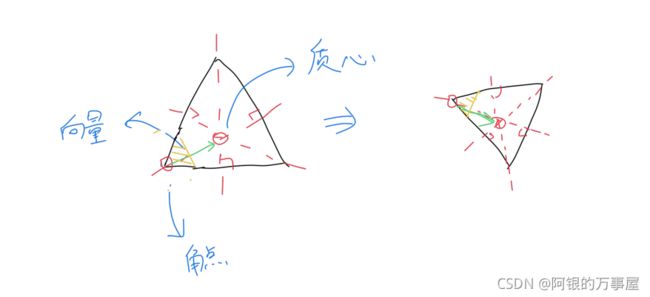
注意标黄三角形区域,可以认为该区域就是brief描述子工作区域,在将工作区域旋转至垂直质心与角点连接向量后,前后两张图工作区域是相同的。这就是为什么引入方向后可以保证brief描述子的旋转一致性(此外,brief描述子虽然是在空间中随机选择匹配点判断像素值大小并生成,但是对于同一批描述子生成时,将采用同一批(p,q)值,才能够保证相同匹配)
更详细地解读和理解,可以参考这篇博客:ORB:FAST关键点和rBRIEF描述子
2. 原理说明&代码解析:结合PnP和ICP的原理和代码,形象理解g2o
这一部分更多的不是代码的详细解读,而是将PnP和ICP结合起来,并依据对g2o的分析,同时加深对PnP,ICP,g2o的理解。
这一部分将通过以下结构组织内容:
- 分析g2o的节点和边类
- PnP和ICP所得雅各比矩阵的实质,区别与联系
- 如何利用g2o来表示PnP和ICP的结合问题
首先通过g2o的代码,分析其节点和边类:
节点类VertexSE3Expmap以及VertexSBAPointXYZ
/* VertexSE3Expmap */
class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
VertexSE3Expmap();
bool read(std::istream& is);
bool write(std::ostream& os) const;
virtual void setToOriginImpl() {
_estimate = SE3Quat();
}
virtual void oplusImpl(const number_t* update_) {
Eigen::Map<const Vector6> update(update_);
setEstimate(SE3Quat::exp(update)*estimate());
}
};
c++最麻烦的就是类的继承重写引用,看起来实在是非常麻烦,所以我一般都是结合使用来理解的,该类的使用例子如下:
g2o::VertexSE3Expmap∗ pose = new g2o::VertexSE3Expmap(); // camera pose
Eigen::Matrix3d R_mat;
R_mat <<
R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2),
R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2),
R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2);
pose−>setId(0);
pose−>setEstimate( g2o::SE3Quat(
R_mat,
Eigen::Vector3d( t.at<double>(0,0), t.at<double>(1,0), t.at<double>(2,0))
) );
optimizer.addVertex( pose );
首先定义一个VertexSE3Expmap类的变量,然后定义李代数并传入pose的setEstimate()函数,即设定了VertexSE3Expmap的测量值,这样就好理解了。
再来看看边类EdgeProjectXYZ2UV,这就更有意思了:
/* EdgeProjectXYZ2UV */
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public BaseBinaryEdge<2, Vector2, VertexSBAPointXYZ, VertexSE3Expmap>{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeProjectXYZ2UV();
bool read(std::istream& is);
bool write(std::ostream& os) const;
void computeError() {
const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
const CameraParameters * cam
= static_cast<const CameraParameters *>(parameter(0));
Vector2 obs(_measurement);
_error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
}
virtual void linearizeOplus();
CameraParameters * _cam;
};
/* linearizeOplus */
void EdgeProjectXYZ2UV::linearizeOplus() {
VertexSE3Expmap ∗ vj = static_cast<VertexSE3Expmap ∗>(_vertices[1]);
SE3Quat T(vj−>estimate());
VertexSBAPointXYZ∗ vi = static_cast<VertexSBAPointXYZ∗>(_vertices[0]);
Vector3D xyz = vi−>estimate();
Vector3D xyz_trans = T.map(xyz);
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
double z_2 = z∗z;
const CameraParameters ∗ cam = static_cast<const CameraParameters ∗>(parameter(0));
Matrix<double,2,3,Eigen::ColMajor> tmp;
tmp(0,0) = cam−>focal_length;
tmp(0,1) = 0;
tmp(0,2) = −x/z∗cam−>focal_length;
tmp(1,0) = 0;
tmp(1,1) = cam−>focal_length;
tmp(1,2) = −y/z∗cam−>focal_length;
_jacobianOplusXi = −1./z ∗ tmp ∗ T.rotation().toRotationMatrix();
_jacobianOplusXj(0,0) = x∗y/z_2 ∗cam−>focal_length;
_jacobianOplusXj(0,1) = −(1+(x∗x/z_2)) ∗cam−>focal_length;
_jacobianOplusXj(0,2) = y/z ∗cam−>focal_length;
_jacobianOplusXj(0,3) = −1./z ∗cam−>focal_length;
_jacobianOplusXj(0,4) = 0;
_jacobianOplusXj(0,5) = x/z_2 ∗cam−>focal_length;
_jacobianOplusXj(1,0) = (1+y∗y/z_2) ∗cam−>focal_length;
_jacobianOplusXj(1,1) = −x∗y/z_2 ∗cam−>focal_length;
_jacobianOplusXj(1,2) = −x/z ∗cam−>focal_length;
_jacobianOplusXj(1,3) = 0;
_jacobianOplusXj(1,4) = −1./z ∗cam−>focal_length;
_jacobianOplusXj(1,5) = y/z_2 ∗cam−>focal_length;
}
该类的使用例子如下:
g2o::EdgeProjectXYZ2UV∗ edge = new g2o::EdgeProjectXYZ2UV();
edge−>setId( index );
edge−>setVertex( 0, dynamic_cast<g2o::VertexSBAPointXYZ∗> (optimizer.vertex(index)) );
edge−>setVertex( 1, pose );
edge−>setMeasurement( Eigen::Vector2d( p.x, p.y ) );
edge−>setParameterId(0,0);
edge−>setInformation( Eigen::Matrix2d::Identity() );
optimizer.addEdge(edge);
总结来说,使用边类的流程就是:定义边类->设定ID->定义先设节点->定义后设节点->定义测量值->定义相机参数ID(来源于设定相机参数时)->定义权重信息(分别对应X,Y,Z)->加入优化器
在边类中,有几个很重要的预定义量,我们这里把它们列举出来:
- _point:表示传入值
- _measurement:表示测量值
- _vertices:节点,index=0对应先设节点,index=1对应后设节点
- _jacobianOplusXi:先设节点的雅各比矩阵
- _jacobianOplusXj:后设节点的雅各比矩阵
有了这些预定义量的认知,我们可以借此实现自定义边的操作,正如ICP实践中EdgeProjectXYZRGBDPoseOnly所做的一样:
/* EdgeProjectXYZRGBDPoseOnly */
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, g2o::VertexSE3Expmap>
{
public: EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeProjectXYZRGBDPoseOnly( const Eigen::Vector3d& point ) :
_point(point) {}
virtual void computeError()
{
const g2o::VertexSE3Expmap∗ pose = static_cast<const g2o::VertexSE3Expmap∗> ( _vertices[0] );
// measurement is p, point is p'
_error = _measurement - pose->estimate() * _point;
}
virtual void linearizeOplus()
{
g2o::VertexSE3Expmap∗ pose = static_cast<g2o::VertexSE3Expmap ∗>(_vertices[0]);
g2o::SE3Quat T(pose−>estimate());
Eigen::Vector3d xyz_trans = T * _point;
double x = xyz_trans[0];
double y = xyz_trans[1];
double z = xyz_trans[2];
_jacobianOplusXi(0,0) = 0;
_jacobianOplusXi(0,1) = −z;
_jacobianOplusXi(0,2) = y;
_jacobianOplusXi(0,3) = −1;
_jacobianOplusXi(0,4) = 0;
_jacobianOplusXi(0,5) = 0;
_jacobianOplusXi(1,0) = z;
_jacobianOplusXi(1,1) = 0;
_jacobianOplusXi(1,2) = −x;
_jacobianOplusXi(1,3) = 0;
_jacobianOplusXi(1,4) = −1;
_jacobianOplusXi(1,5) = 0;
_jacobianOplusXi(2,0) = −y;
_jacobianOplusXi(2,1) = x;
_jacobianOplusXi(2,2) = 0;
_jacobianOplusXi(2,3) = 0;
_jacobianOplusXi(2,4) = 0;
_jacobianOplusXi(2,5) = −1;
}
bool read ( istream& in ) {}
bool write ( ostream& out ) const {}
protected: Eigen::Vector3d _point;
};
由于ICP中定义的边只需要连接第二个相机位姿一个节点(第一个相机位姿在这里被假定为固定的,不做修改,所以不是节点),所以vertices的index只有一个
已知这一内容,再结合我们列举的预设定量,就可以像上面一样重写边类了。
综上,第一部分内容我们就介绍完毕了,主要针对g2o的节点类和边类的定义以及如何使用做了介绍,同时还深入研究了如何重写一个g2o的边类,以应对不同的连接要求和雅各比计算要求。
接下来,进一步对PnP和ICP所得雅各比矩阵的实质,区别与联系做介绍:
明确:
ICP 3D-3D误差求导的雅各比矩阵 J J J是3*6维的
PnP 3D-2D重投影误差求导的雅各比矩阵 J J J是2*6维的
说明:
3D-3D误差和3D-2D重投影误差在求相机位姿的雅各比矩阵时,所有的匹配点求得的雅各比矩阵(同维度)应该叠加在一起后再用于列-马公式,求得两个 Δ x \Delta x Δx,分别求得的 Δ x \Delta x Δx再加在一起(求导结果可加性)确定最终下降结果(可以误差和重投影误差的 Δ x \Delta x Δx不相同,这样就相当于依次处理不同变量的梯度,而实际上两者是相同的,所以可以直接叠加)
与之相对,在特征点误差上,每个特征点本次更新的 Δ x \Delta x Δx又是分开的,因为不同特征点确实对应着不同的变量(其空间坐标)
即:
PnP问题将得到两类雅各比矩阵,第一类是相机位姿对应的雅各比矩阵,维数是2*6维,第二类是空间点对应的雅各比矩阵,维数是2*3维,前者是唯一的,而后者针对不同的空间点有不同的形式。
ICP问题仅得到一类雅各比矩阵,即相机位姿对应的雅各比矩阵,我们也称之为第一类,它是3*6维的
最后,如何利用g2o来表示PnP和ICP的结合问题:
结合问题,顾名思义就是对深度明确的匹配点,使用3D-3D误差,对于深度不明的匹配点,使用3D-2D重投影误差,如何在g2o中表示这个结合问题的优化图?
前提:
实践PnP中,g2o建立了四个节点,3个为空间点,1个为相机位姿,连接图如下:
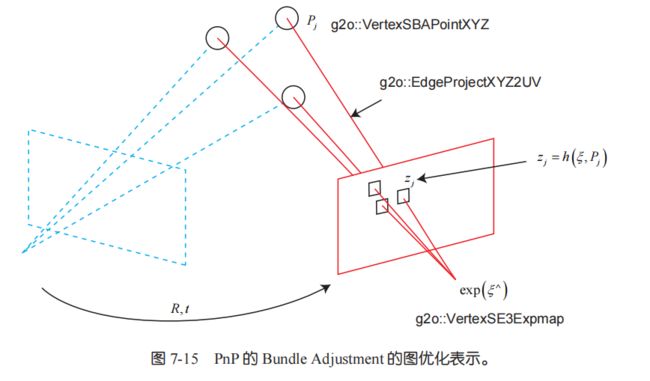
进一步说明:
根据第二部分的解释,我们可以知道对于这四个节点,g2o将分别计算4个雅各比矩阵并最终确定节点下降梯度,其中相机位姿节点对应第一类雅各比矩阵,空间点节点对应第二类雅各比矩阵。这两类雅各比矩阵由重投影点(估计值)以及匹配点归一化坐标(测量值)约束。这就是PnP问题的g2o表示
那么结合ICP后,g2o表示又会变成什么样?
ICP是相机位姿的自连接(也可以看成固定第一个相机位姿节点的位姿图),雅各比矩阵由变化到相机坐标系2后的空间点坐标(估计值)以及原相机坐标系下的空间点坐标(测量值)约束,所以想把ICP加入到上述图中,只需要为相机位姿节点自连接一个自定义的EdgeProjectXYZRGBDPoseOnly边类。
结论:
g2o的节点与雅各比矩阵的关系:
-
g2o的节点对应优化的变量,而优化的变量决定了雅各比矩阵的类型
对应到这个问题中就是:相机位姿节点对应相机位姿优化变量,相机位姿优化变量决定该节点雅各比矩阵类型是第一类
-
g2o边连接了多少个节点,就需要定义多少类雅各比矩阵
对应到这个问题中就是:ICP的边只需要定义一类雅各比矩阵,而PnP的边需要定义两类雅各比矩阵
3. 代码解析:解析高斯牛顿单层光流代码
我们先提取出高斯牛顿实现单层光流中的关键代码:
// compute cost and jacobian
for (int x = -half_patch_size; x < half_patch_size; x++)
for (int y = -half_patch_size; y < half_patch_size; y++) {
double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -
GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy); // Jacobian
if (inverse == false) {
J = -1.0 * Eigen::Vector2d(
0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
);
} else if (iter == 0) {
// in inverse mode, J keeps same for all iterations
// NOTE this J does not change when dx, dy is updated, so we can store it and only compute error
J = -1.0 * Eigen::Vector2d(
0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -
GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),
0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -
GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))
);
}
// compute H, b and set cost;
b += -error * J;
cost += error * error;
if (inverse == false || iter == 0) {
// also update H
H += J * J.transpose();
}
}
我们将对上述部分进行以下的说明:
- 为什么求解出的update是 Δ x \Delta x Δx和 Δ y \Delta y Δy?
- 为什么雅各比矩阵是这样的双层迭代计算?
之所以会问出第一个问题,是因为我们发现,在介绍LK光流的时候,推导过程给出的求解结果是像素移动速度u,v,这显然和 Δ x \Delta x Δx和 Δ y \Delta y Δy不一致,怎么回答这个问题?
我们需要注意的是,一般在处理光流追踪时,都是两张图间。而在前一章的LK推理中,是假设图像是时间的函数
这一个假设可以用 I 1 , I 2 I_1,I_2 I1,I2两个图像来替换掉时间,即可以将等式约束变为:
I 2 ( x + d x , y + d y ) = I 1 ( x , y ) I_2(x+dx, y+dy) = I_1(x, y) I2(x+dx,y+dy)=I1(x,y),去掉时间 t t t
同样,将上式泰勒展开,有:
I 2 ( x + d x , y + d y ) ≈ I 1 ( x , y ) + ∂ I 2 ∂ x d x + ∂ I 2 ∂ y d y I_2(x+dx, y+dy) \approx I_1(x, y)+\frac{\partial I_2}{\partial x}dx+\frac{\partial I_2}{\partial y}dy I2(x+dx,y+dy)≈I1(x,y)+∂x∂I2dx+∂y∂I2dy
进一步,假设:
e r r o r = I 1 ( x , y ) − I 2 ( x + d x , y + d y ) error=I_1(x, y)-I_2(x+dx, y+dy) error=I1(x,y)−I2(x+dx,y+dy)
由灰度不变性假设,当引入 w ∗ w w*w w∗w的窗口后,窗口内的所有像素灰度误差应该最小,即 e r r o r ∗ e r r o r error*error error∗error最小
由于 ∂ I 2 ∂ x d x + ∂ I 2 ∂ y d y = − e r r o r \frac{\partial I_2}{\partial x}dx+\frac{\partial I_2}{\partial y}dy=-error ∂x∂I2dx+∂y∂I2dy=−error
计 ∂ I 2 ∂ x \frac{\partial I_2}{\partial x} ∂x∂I2为 I x I_x Ix, ∂ I 2 ∂ y \frac{\partial I_2}{\partial y} ∂y∂I2为 I y I_y Iy,可以将该式写成矩阵形式:
[ I x , I y ] [ d x d y ] = − e r r o r [I_x, I_y] \left[ \begin{matrix} dx\\ dy \end{matrix} \right]=-error [Ix,Iy][dxdy]=−error
引入 w ∗ w w*w w∗w的窗口,化为最小二乘问题:
设 A = [ [ I x , I y ] 1 ⋮ [ I x , I y ] k ] A=\left[ \begin{matrix} [I_x, I_y]_1\\\vdots\\ [I_x, I_y]_k \end{matrix} \right] A=⎣⎢⎡[Ix,Iy]1⋮[Ix,Iy]k⎦⎥⎤
最小二乘为:
m i n ∣ ∣ A [ d x d y ] ∣ ∣ 2 2 min||A\left[ \begin{matrix} dx\\ dy \end{matrix} \right]||^2_2 min∣∣A[dxdy]∣∣22
所以,求解这一最小二乘的高斯牛顿法,得到的是 d x , d y dx,dy dx,dy的增量
该最小二乘问题的雅各比矩阵为:
J = A T J=A^T J=AT
最小二乘的误差 f ( [ d x d y ] ) = [ − e r r o r 1 ⋮ − e r r o r k ] f(\left[ \begin{matrix} dx\\ dy \end{matrix} \right])=\left[ \begin{matrix} -error_1\\\vdots\\ -error_k \end{matrix} \right] f([dxdy])=⎣⎢⎡−error1⋮−errork⎦⎥⎤
根据上面的改进最小二乘推导,我们可以解释高斯牛顿求解的为什么是 Δ x \Delta x Δx和 Δ y \Delta y Δy的增量了
接下来说明第二个问题,为什么雅各比矩阵是通过双层迭代来求解的?
双层迭代其实是求解矩阵元素和,海塞近似公式为:
H = J J T H=JJ^T H=JJT
我们知道,单一像素的雅各比矩阵为: A [ k ] T A[k]^T A[k]T,即总雅各比矩阵第k列(k为像素标号)
所以对单一像素求海塞近似,再将所有像素海塞近似叠加是等价于总雅各比矩阵直接求海塞近似
同理,求高斯牛顿的右边b,也是一个将总雅各比矩阵乘拆成单一像素雅各比乘后相加的过程
综上所述,我们采用了双层迭代遍历所有像素的方式来求解一个窗口内最小二乘问题的海塞近似H和b
当然,我们仍然可以先用双层迭代生成总雅各比矩阵和总误差向量,再通过矩阵乘得到海塞近似H和b
六、ch9
1. 运行报错:g2o时报"fmt"相关错误
感谢这位博主的精彩讲解,g2o库更新后,需要使用fmt库(以后所有g2o使用时都会有这个问题),所以需要修正CMAKELIST.txt文件,将fmt头文件包含进来
target_link_libraries(bundle_adjustment_g2o ${G2O_LIBS} bal_common fmt)
如上所示,在最后一句连接lib的代码中加入fmt即可
七、ch13
1. 运行报错:can not be used when making a shared object; recompile with -fPIC
这个问题一定要注意看是哪个包无法分享而导致的需要recompile,我这里是fmt这个包,所以解决办法就是重新下载fmt,重新编译,如果在cmake过程中实现-fPIC编译可以参考这篇博客如何解决fPIC
我在这里简单的复制一下博主所说:
对于cmake生成的makefile则可以在CMakeList.txt或者cmake生成的CMakeCache.txt中加上-fPIC,CMAKE_CXX_FLAGS:STRING=-fPIC,CMAKE_C_FLAGS:STRING=-fPIC,CMAKE_EXE_LINKER_FLAGS:STRING=-fPIC
修改之后记得重新make和sudo make install,然后会发现无法分享的问题已经解决
2. 代码解析:13讲实现中涉及到的并行编程
关联头文件:
:原子类型,可以被不同线程同时访问而不报错 :包含mutex系列类和lock系列类,完成互斥量声明与锁控制功能 :条件变量类,主要通过类函数wait()和notify_one()管理激活和阻塞 :13讲中未涉及到这个头文件相关,所以不展开
我们截取13讲中的一小段代码展开介绍这部分内容:
// backend类声明
class Backend {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
typedef std::shared_ptr<Backend> Ptr;
/// 构造函数中启动优化线程并挂起
Backend(){
backend_running_.store(true); // 设置原子类型值
backend_thread_ = std::thread(std::bind(&Backend::BackendLoop, this)); // 由于是有参创建线程,所以自动join
};
/// 触发地图更新,启动优化
void UpdateMap(){
std::unique_lock<std::mutex> lock(data_mutex_);
map_update_.notify_one(); // 启动backend线程
}
/// 停止线程
void Stop(){
backend_running_.store(false);
map_update_.notify_one();
backend_thread_.join(); // 再次调用join关闭线程
}
private:
/// 后端线程
void BackendLoop(){
while (backend_running_.load()) { // 读取原子类型值
std::unique_lock<std::mutex> lock(data_mutex_);
map_update_.wait(lock); //锁住当前线程
// 省略优化函数撰写
}
}
std::thread backend_thread_;
std::mutex data_mutex_;
std::condition_variable map_update_;
std::atomic<bool> backend_running_;
}
// frame类声明
struct Frame {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
typedef std::shared_ptr<Frame> Ptr;
SE3 pose_; // Tcw 形式Pose
std::mutex pose_mutex_; // Pose数据锁
Frame(){}
// set, thread safe
void SetPose(const SE3 &pose) {
std::unique_lock<std::mutex> lck(pose_mutex_); // unique_lock实现了如果可以访问,则获得互斥锁,如果暂时不能访问,则访问线程阻塞,直到可以获得互斥锁;还实现了访问结束自动释放互斥锁
pose_ = pose;
}
};
// 声明backend线程,启动backend线程,关闭backend线程,安全访问frame
void main(){
backend_ = Backend::Ptr(new Backend);
frame = Frame::Ptr(new Frame);
backend_->UpdateMap(); // 通过UpdateMap()激活条件变量,解除线程的阻塞
frame->SetPose(new SE3::pose);
backend_->Stop();
}
backend和frame类我做了一些调整,只保留了基础设置以及和多线程有关的设定,总体而言就是:
- 线程的阻塞和挂起可以通过条件变量实现
- 对线程的访问可以通过unique_lock自动控制