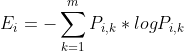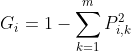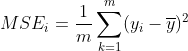决策树（Decision Tree）

一、理论介绍 

决策树(Decision Tree，DT)，亦称“判定树”，是以实例为基础的归纳学习算法，它根据样本的特征，按照一定规则将无序的样本分裂成不同的分支，从而达到分类或回归的目的。其最早由Hunt E于1966年提出[1]。

1.1决策树的生成

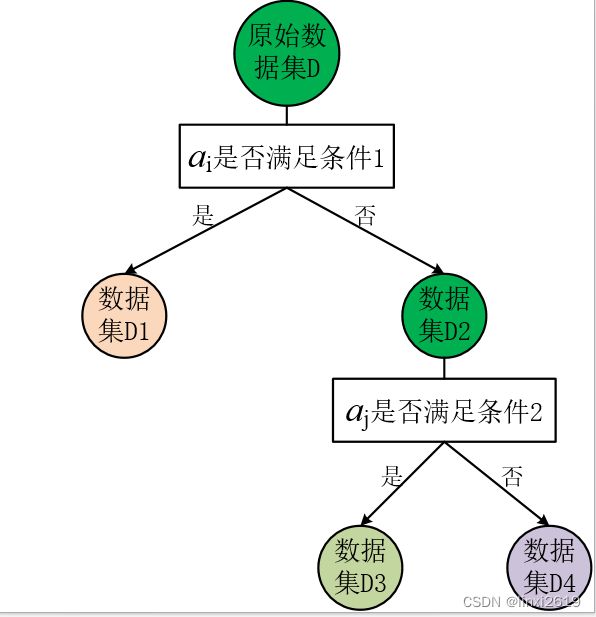
使用决策树算法进行分类或回归通常有三个步骤：特征选择、决策树的生成、决策树的修剪。对于具有m个样本的数据集 ，即每个样本有n个特征，K个标签，假设其特征属性为 ，样本标签为 ，则决策树的建立过程如图 1所示。

 图1 决策树的建立

图 1为一棵具有两层深度的决策树，其中原始数据集D为根节点，然后选择一个最优特征，按这一特征将训练数据集分割成两个互斥的子集，使得各个子集有一个在当前条件下最好的分类。如果这一子集中的样本已经被正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去(数据集D1)。若子集不能够被正确的分类，那么就对此子集选择新的最优特征，继续对其进行分割，构建相应的节点，如此递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

最优特征的选择与子集的划分通过贪心算法进行，每次分裂都是使当前子集的“纯度”变高。为了表述分裂前后子集的“纯度”的变化引进信息增益的概念，所谓信息增益是指分裂后“纯度”度量指标的变化量。在分类问题中度量样本集合纯度的指标有信息熵(Information Entropy)和基尼指数(Gini index)，二者的定义如式1和式2所示。在回归问题中度量指标是均方误差(Mean Square Error，MSE)，其表达式如式3所示。

                                                               式1 

                                                                           式2      

                                                              式3

式中， 为第i个节点上，类别为k的样本占比；m为第i个节点上所有的样本数量； 为第k个样本的标签值； 为第i个节点上所有样本的平均值。

根据度量样本集合纯度指标的不同，用于训练决策树的常见算法有如CLS[2]、ID3[3]、C4.5[4]、CART[5]等。其中目前最流行的为分类与回归树(Classification And Regression Tree，CART)，基本思想是：首先，使用单个特征k和其阈值 ，将原始训练集分成两个子集，然后在每个子集中重复上述过程，直至满足某些条件不再分裂。特征k和 的选择应使得分裂后子集的纯度更高或者MSE更小，所以对于分类问题，CART的成本函数为式4，对于回归问题，CART的成本函数如式5所示。

                                                                                                  式4

                                           式5

式中，,分别为与两个子集对应的输出，一般为各子集对应的均值。

1.2决策树的修剪

若不对决策树的生长过程进行任何限制，则其将会为了更好的拟合训练集数据将过度生长。理论上一棵未加任何限制的决策树可实现对训练数据100%的完美拟合，只要特征空间的划分足够密集，保证每个样本分为一类就可实现对训练数据的完美拟合。但是过拟合的决策树泛化性能往往比较差，因此为了提高决策树模型的泛化能力，需要采取一定的手段对决策树的生长过程进行限制，防止其由于过度生长而出现过拟合的情况。剪枝 (pruning)处理是防止决策树模型过拟合的主要手段，决策树剪枝的基本策略有预剪枝(pre_pruning)和后剪枝(post_pruning)[6]两种。

预剪枝是指在决策树生成过程中，每个结点分裂之前评估分裂是否能够提升模型的泛化性能，若某一结点的分裂不能使模型的泛化性能提升，则停止分裂并将当前结点作为叶子结点。后剪枝是指先不加任何约束使用训练集训练一颗决策树，然后自底向上对非叶子结点进行评估，若将某一结点对应的子树替换为叶子结点可使模型的泛化性能提升，则将该结点作为叶子结点。

二、实例

利用scikit-learn库中的Decision Tree对鸢尾花数据集进行分类，其中决策树中的超参数均为默认 参数，要想了解更多超参数优化的内容，可参考后续的优化算法专栏。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score

import numpy as np
import matplotlib.pyplot as plt

# Parameters
n_classes = 3
plot_colors = "ryb"
plot_step = 0.02

#load iris dataset
iris = load_iris()

#fit the model with petal length  and petal width
X = iris.data[:, [2,3]]
y = iris.target

#split the iris dataset to two parts
train_x, test_x, train_y, test_y = train_test_split(X, y, train_size=0.8, random_state=0)

#train
clf = DecisionTreeClassifier(random_state=0)
clf.fit(train_x, train_y)

#predict
pred_y = clf.predict(test_x)
score = accuracy_score(test_y,pred_y)
print(score)  #the accuracy in test set

# Plot the decision boundary
ax = plt.subplot(1,1,1)
#plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)
DecisionBoundaryDisplay.from_estimator(
    clf,
    X,
    cmap=plt.cm.RdYlBu,
    response_method="predict",
    ax=ax,
    xlabel=iris.feature_names[2],
    ylabel=iris.feature_names[3],
)

 # Plot the training points
for i, color in zip(range(n_classes), plot_colors):
    idx = np.where(y == i)
    plt.scatter(
        X[idx, 0],
        X[idx, 1],
        c=color,
        label=iris.target_names[i],
        cmap=plt.cm.RdYlBu,
        edgecolor="black",
        s=15,
    )
plt.show()

# Display the structure of a single decision tree trained on all the features
from sklearn.tree import plot_tree

plt.figure()
clf = DecisionTreeClassifier().fit(iris.data, iris.target)
plot_tree(clf, filled=True)
plt.title("Decision tree trained on all the iris features")
plt.show()

在此实例中采用鸢尾花数据集，鸢尾花数据集中总共有150各样本，每个样本有四个特征，一个分类标签，总共有三各类，每个类有50个样本。其中各样本的属性保存在iris.data中，标签保存在iris.target中，三个类对应的标签分别为0，1，2。

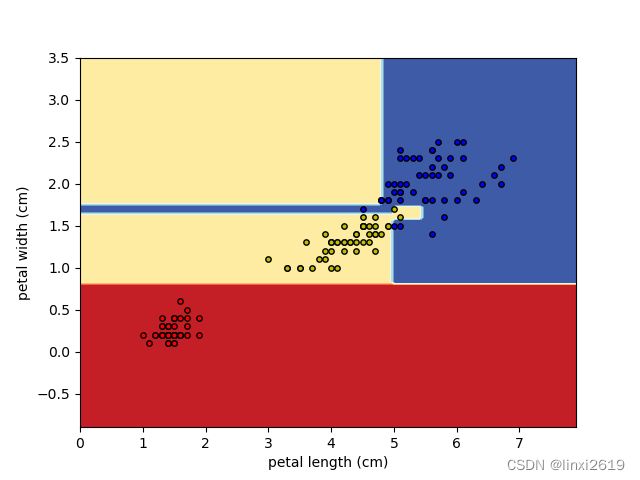
其中各分类决策边界如图2所示，决策树在所有数据的生长如图3所示。这两个图的相关代码参考了scikit-learn官方文档中的样例。

                              图2 决策边界                                                      图3 决策树的生长

 其中查看决策树的生长过程还有另一种方法：

安装 Graphviz： Graphviz

配置环境变量

from sklearn import tree

# Visualize model
with open("iris_tree.dot", 'w') as f:
    f = tree.export_graphviz(clf, feature_names=iris.feature_names, out_file=f)

在命令行窗口转到当前目录，然后通过下面命令将.dot文件转换为.png文件，如图4所示。

转化dot文件至png可视化决策树：dot -Tpng iris_tree.dot -o iris_tree.png 

 图4 决策树可视化

三、参考文献

1. Hunt E.Utilization of memory in concept learning systems[J]. Utilization of Memory in Concept Learning Systems，1966，(4)：42-48.
2. J，R，Quinlan．Induction of decision trees[J]．Machine Learning，1986，48(2)：214-219.
3. Quinlan J R．C4.5:Programs for Machine Learning[J]．Machine Learning, 1993，16(3):235-240.
4. Breiman L，Friedman J H，Olshen R A．Classification and Regression Trees(CART)[J]．Biometrics，1984，40(3)：358.